
Question Number 83899 by john santu last updated on 07/Mar/20
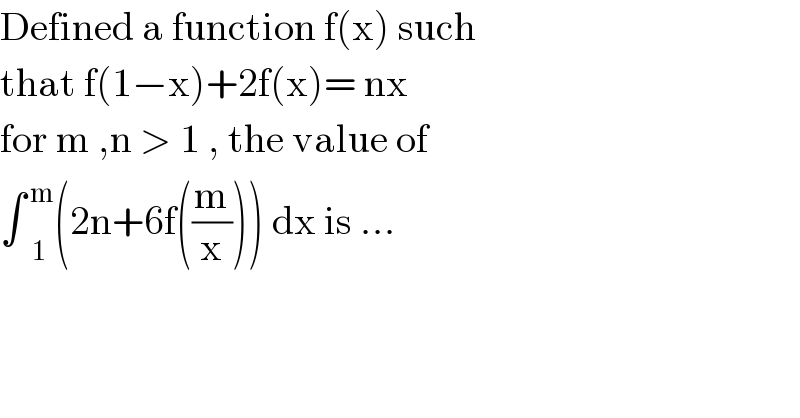
$$\mathrm{Defined}\:\mathrm{a}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{such}\: \\ $$ $$\mathrm{that}\:\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right)+\mathrm{2f}\left(\mathrm{x}\right)=\:\mathrm{nx}\: \\ $$ $$\mathrm{for}\:\mathrm{m}\:,\mathrm{n}\:>\:\mathrm{1}\:,\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$ $$\int\underset{\mathrm{1}} {\overset{\:\mathrm{m}} {\:}}\left(\mathrm{2n}+\mathrm{6f}\left(\frac{\mathrm{m}}{\mathrm{x}}\right)\right)\:\mathrm{dx}\:\mathrm{is}\:... \\ $$
Commented byjohn santu last updated on 07/Mar/20
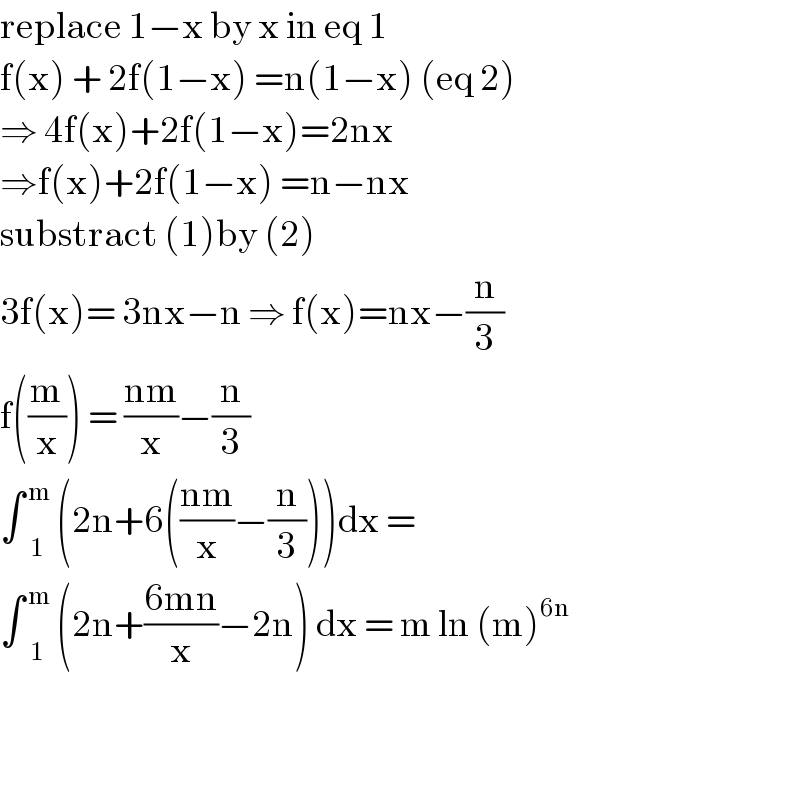
$$\mathrm{replace}\:\mathrm{1}−\mathrm{x}\:\mathrm{by}\:\mathrm{x}\:\mathrm{in}\:\mathrm{eq}\:\mathrm{1} \\ $$ $$\mathrm{f}\left(\mathrm{x}\right)\:+\:\mathrm{2f}\left(\mathrm{1}−\mathrm{x}\right)\:=\mathrm{n}\left(\mathrm{1}−\mathrm{x}\right)\:\left(\mathrm{eq}\:\mathrm{2}\right) \\ $$ $$\Rightarrow\:\mathrm{4f}\left(\mathrm{x}\right)+\mathrm{2f}\left(\mathrm{1}−\mathrm{x}\right)=\mathrm{2nx} \\ $$ $$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)+\mathrm{2f}\left(\mathrm{1}−\mathrm{x}\right)\:=\mathrm{n}−\mathrm{nx} \\ $$ $$\mathrm{substract}\:\left(\mathrm{1}\right)\mathrm{by}\:\left(\mathrm{2}\right) \\ $$ $$\mathrm{3f}\left(\mathrm{x}\right)=\:\mathrm{3nx}−\mathrm{n}\:\Rightarrow\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{nx}−\frac{\mathrm{n}}{\mathrm{3}} \\ $$ $$\mathrm{f}\left(\frac{\mathrm{m}}{\mathrm{x}}\right)\:=\:\frac{\mathrm{nm}}{\mathrm{x}}−\frac{\mathrm{n}}{\mathrm{3}} \\ $$ $$\int\underset{\mathrm{1}} {\overset{\:\mathrm{m}} {\:}}\:\left(\mathrm{2n}+\mathrm{6}\left(\frac{\mathrm{nm}}{\mathrm{x}}−\frac{\mathrm{n}}{\mathrm{3}}\right)\right)\mathrm{dx}\:= \\ $$ $$\int\underset{\mathrm{1}} {\overset{\:\mathrm{m}} {\:}}\:\left(\mathrm{2n}+\frac{\mathrm{6mn}}{\mathrm{x}}−\mathrm{2n}\right)\:\mathrm{dx}\:=\:\mathrm{m}\:\mathrm{ln}\:\left(\mathrm{m}\right)^{\mathrm{6n}} \\ $$ $$ \\ $$ $$ \\ $$
