Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 209162 by dr1001sa last updated on 02/Jul/24

Cyclic quadrilateral ABCD is inscribed in circle. Point S is intersection of diagonals AC and BD (S is not center of the circle). If AB=BC=6 and BS=4, what is length of BD?

$$ \\ $$Cyclic quadrilateral ABCD is inscribed in circle. Point S is intersection of diagonals AC and BD (S is not center of the circle). If AB=BC=6 and BS=4, what is length of BD?

Answered by mr W last updated on 02/Jul/24

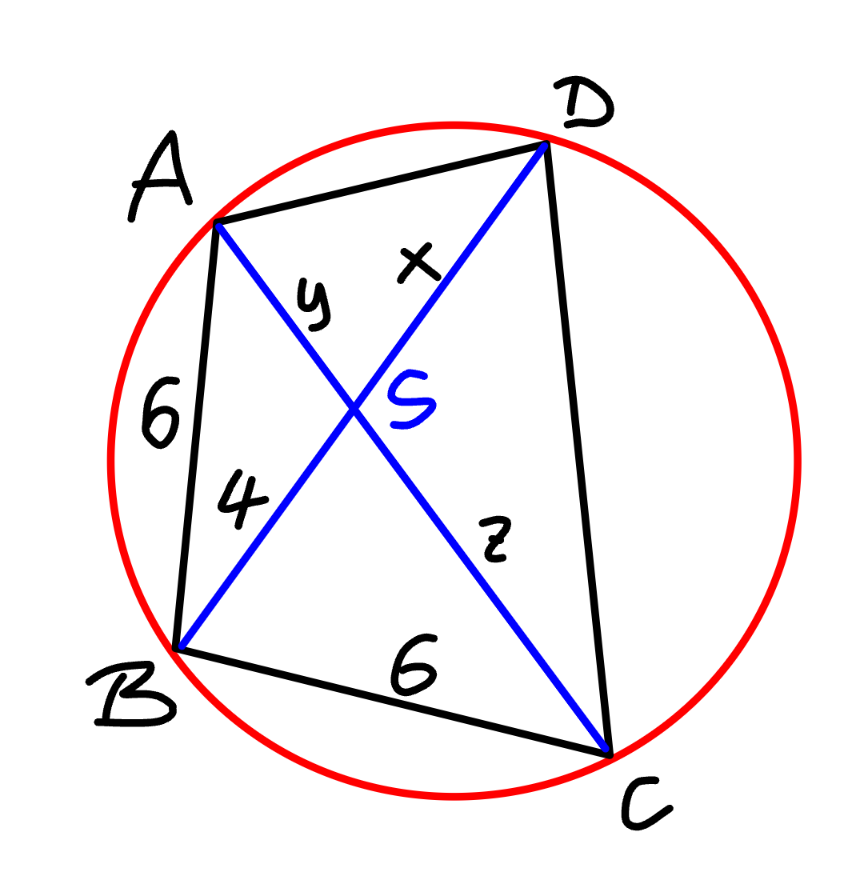
Commented by mr W last updated on 03/Jul/24

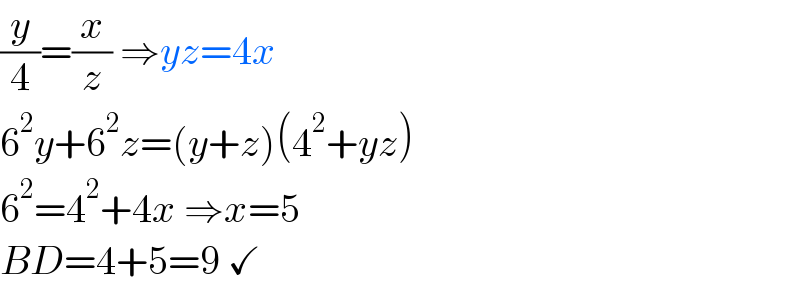
(y/4)=(x/z) ⇒yz=4x 6^2 y+6^2 z=(y+z)(4^2 +yz) 6^2 =4^2 +4x ⇒x=5 BD=4+5=9 ✓

$$\frac{{y}}{\mathrm{4}}=\frac{{x}}{{z}}\:\Rightarrow{yz}=\mathrm{4}{x} \\ $$$$\mathrm{6}^{\mathrm{2}} {y}+\mathrm{6}^{\mathrm{2}} {z}=\left({y}+{z}\right)\left(\mathrm{4}^{\mathrm{2}} +{yz}\right) \\ $$$$\mathrm{6}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\mathrm{4}{x}\:\Rightarrow{x}=\mathrm{5}\: \\ $$$${BD}=\mathrm{4}+\mathrm{5}=\mathrm{9}\:\checkmark \\ $$

Commented by efronzo1 last updated on 03/Jul/24

(i) ⋮D♠Z⪅𝛎

$$\:\:\left(\mathrm{i}\right)\:\:\underline{\vdots}\underbrace{\mathfrak{D}\spadesuit\boldsymbol{\mathrm{Z}}\lessapprox\boldsymbol{\nu}} \\ $$

Commented by dr1001sa last updated on 03/Jul/24

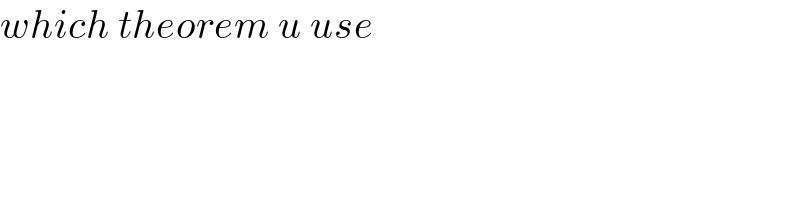
which theorem u use

$${which}\:{theorem}\:{u}\:{use} \\ $$

Commented by mr W last updated on 03/Jul/24

Commented by mr W last updated on 03/Jul/24

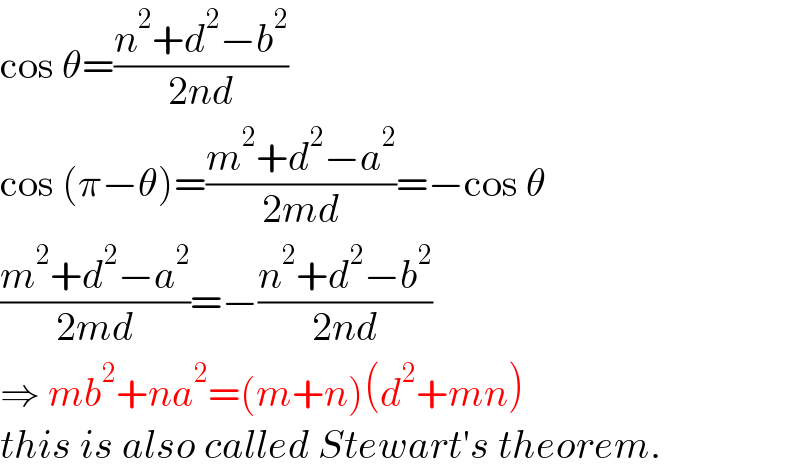
cos θ=((n^2 +d^2 −b^2 )/(2nd)) cos (π−θ)=((m^2 +d^2 −a^2 )/(2md))=−cos θ ((m^2 +d^2 −a^2 )/(2md))=−((n^2 +d^2 −b^2 )/(2nd)) ⇒ mb^2 +na^2 =(m+n)(d^2 +mn) this is also called Stewart′s theorem.

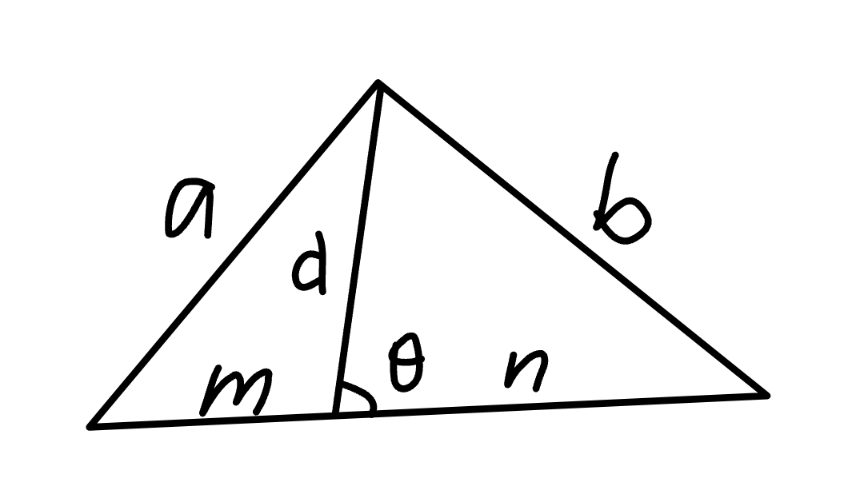
$$\mathrm{cos}\:\theta=\frac{{n}^{\mathrm{2}} +{d}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{nd}} \\ $$$$\mathrm{cos}\:\left(\pi−\theta\right)=\frac{{m}^{\mathrm{2}} +{d}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{md}}=−\mathrm{cos}\:\theta \\ $$$$\frac{{m}^{\mathrm{2}} +{d}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{md}}=−\frac{{n}^{\mathrm{2}} +{d}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{nd}} \\ $$$$\Rightarrow\:{mb}^{\mathrm{2}} +{na}^{\mathrm{2}} =\left({m}+{n}\right)\left({d}^{\mathrm{2}} +{mn}\right) \\ $$$${this}\:{is}\:{also}\:{called}\:{Stewart}'{s}\:{theorem}. \\ $$

Commented by dr1001sa last updated on 03/Jul/24

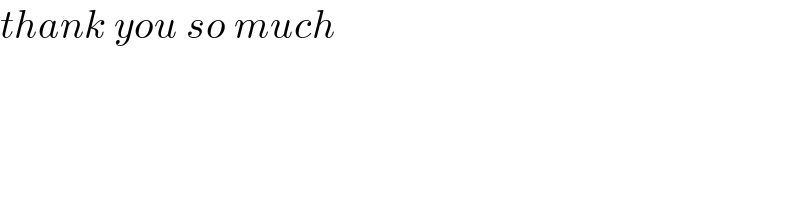
thank you so much

$${thank}\:{you}\:{so}\:{much} \\ $$

Answered by A5T last updated on 02/Jul/24

Commented by A5T last updated on 02/Jul/24

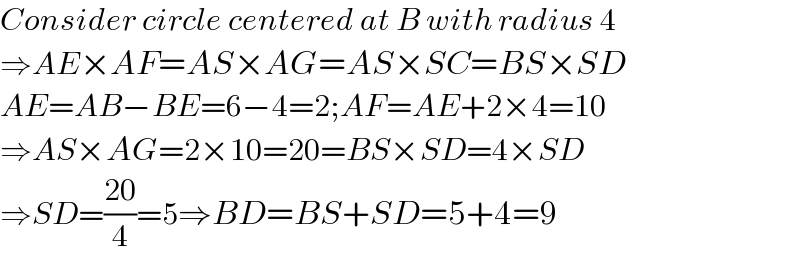
Consider circle centered at B with radius 4 ⇒AE×AF=AS×AG=AS×SC=BS×SD AE=AB−BE=6−4=2;AF=AE+2×4=10 ⇒AS×AG=2×10=20=BS×SD=4×SD ⇒SD=((20)/4)=5⇒BD=BS+SD=5+4=9

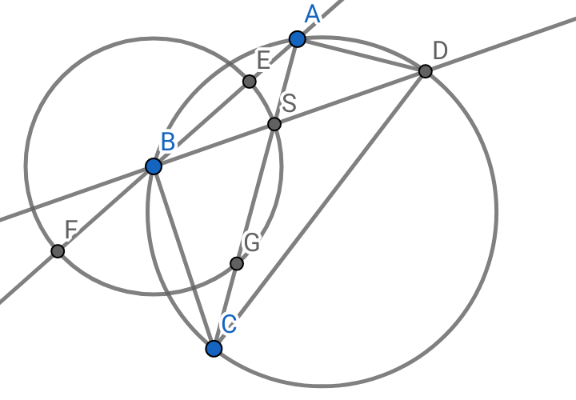
$${Consider}\:{circle}\:{centered}\:{at}\:{B}\:{with}\:{radius}\:\mathrm{4} \\ $$$$\Rightarrow{AE}×{AF}={AS}×{AG}={AS}×{SC}={BS}×{SD} \\ $$$${AE}={AB}−{BE}=\mathrm{6}−\mathrm{4}=\mathrm{2};{AF}={AE}+\mathrm{2}×\mathrm{4}=\mathrm{10} \\ $$$$\Rightarrow{AS}×{AG}=\mathrm{2}×\mathrm{10}=\mathrm{20}={BS}×{SD}=\mathrm{4}×{SD} \\ $$$$\Rightarrow{SD}=\frac{\mathrm{20}}{\mathrm{4}}=\mathrm{5}\Rightarrow{BD}={BS}+{SD}=\mathrm{5}+\mathrm{4}=\mathrm{9} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com