
Question Number 47224 by hassentimol last updated on 06/Nov/18
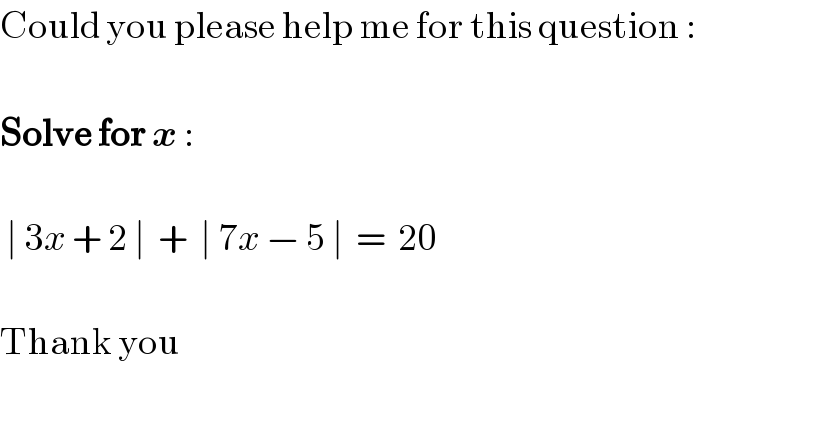
$$\mathrm{Could}\:\mathrm{you}\:\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{for}\:\mathrm{this}\:\mathrm{question}\:: \\ $$$$ \\ $$$$\boldsymbol{\mathrm{Solve}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{{x}}\:: \\ $$$$ \\ $$$$\:\mid\:\mathrm{3}{x}\:+\:\mathrm{2}\:\mid\:\:+\:\:\mid\:\mathrm{7}{x}\:−\:\mathrm{5}\:\mid\:\:=\:\:\mathrm{20} \\ $$$$ \\ $$$$\mathrm{Thank}\:\mathrm{you} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 06/Nov/18
![let first eradicte the absolut value x −∞ −(2/3) (5/7) +∞ ∣3x+2∣ −3x−2 0 3x+2 3x+2 ∣7x−5∣ −7x +5 −7x+5 0 7x +5 A(x) −10x+3 −4x +7 10x +7 equ. ⇔ A(x)=20 case 1 x ∈]−∞,−(2/3)] A(x)=20 ⇔−10x +3 =20 ⇔−10x =17 ⇔x=−((17)/(10)) −((17)/(10)) +(2/3) =((−34+20)/(30)) =((−14)/(30))<0 ⇒ −((17)/(10))<−(2/3) so the number is solution case 2 x ∈[−(2/3) ,(5/7)] A(x)=20 ⇔ −4x+7 =20 ⇔−4x =13 ⇔x=−((13)/4) −((13)/4) +(2/3)<0 ⇒−((13)/4)<−(2/3) so this number is nt solution case 3 x∈[(5/7),+∞[A(x)=20 ⇔ 10x +7 =20 ⇔10x =13 ⇔x=((13)/(10)) ((13)/(10)) −(5/7) =((13.7 −50)/(70))>0 ⇒((13)/(10))>(5/7) so this number is solution so the (e) have 2 solutions −((17)/(10)) and (5/7) . ∣](Q47245.png)
$${let}\:{first}\:{eradicte}\:{the}\:{absolut}\:{value} \\ $$$${x}\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{5}}{\mathrm{7}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$$$\mid\mathrm{3}{x}+\mathrm{2}\mid\:\:\:\:\:\:−\mathrm{3}{x}−\mathrm{2}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{3}{x}+\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{3}{x}+\mathrm{2} \\ $$$$\mid\mathrm{7}{x}−\mathrm{5}\mid\:\:−\mathrm{7}{x}\:\:\:+\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{7}{x}+\mathrm{5}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{7}{x}\:+\mathrm{5} \\ $$$${A}\left({x}\right)\:\:\:\:\:\:\:\:\:−\mathrm{10}{x}+\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{4}{x}\:+\mathrm{7}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{10}{x}\:+\mathrm{7} \\ $$$${equ}.\:\Leftrightarrow\:{A}\left({x}\right)=\mathrm{20} \\ $$$$\left.{c}\left.{ase}\:\mathrm{1}\:\:\:\:\:\:{x}\:\in\right]−\infty,−\frac{\mathrm{2}}{\mathrm{3}}\right]\:\:\:\:{A}\left({x}\right)=\mathrm{20}\:\Leftrightarrow−\mathrm{10}{x}\:+\mathrm{3}\:=\mathrm{20}\:\Leftrightarrow−\mathrm{10}{x}\:=\mathrm{17}\:\Leftrightarrow{x}=−\frac{\mathrm{17}}{\mathrm{10}} \\ $$$$−\frac{\mathrm{17}}{\mathrm{10}}\:+\frac{\mathrm{2}}{\mathrm{3}}\:=\frac{−\mathrm{34}+\mathrm{20}}{\mathrm{30}}\:=\frac{−\mathrm{14}}{\mathrm{30}}<\mathrm{0}\:\Rightarrow\:−\frac{\mathrm{17}}{\mathrm{10}}<−\frac{\mathrm{2}}{\mathrm{3}}\:{so}\:{the}\:{number}\:{is}\:{solution} \\ $$$${case}\:\mathrm{2}\:\:{x}\:\in\left[−\frac{\mathrm{2}}{\mathrm{3}}\:,\frac{\mathrm{5}}{\mathrm{7}}\right]\:{A}\left({x}\right)=\mathrm{20}\:\Leftrightarrow\:−\mathrm{4}{x}+\mathrm{7}\:=\mathrm{20}\:\Leftrightarrow−\mathrm{4}{x}\:=\mathrm{13}\:\Leftrightarrow{x}=−\frac{\mathrm{13}}{\mathrm{4}} \\ $$$$−\frac{\mathrm{13}}{\mathrm{4}}\:+\frac{\mathrm{2}}{\mathrm{3}}<\mathrm{0}\:\Rightarrow−\frac{\mathrm{13}}{\mathrm{4}}<−\frac{\mathrm{2}}{\mathrm{3}}\:{so}\:{this}\:{number}\:{is}\:{nt}\:{solution} \\ $$$${case}\:\mathrm{3}\:\:\:\:\:{x}\in\left[\frac{\mathrm{5}}{\mathrm{7}},+\infty\left[{A}\left({x}\right)=\mathrm{20}\:\Leftrightarrow\:\:\mathrm{10}{x}\:+\mathrm{7}\:=\mathrm{20}\:\Leftrightarrow\mathrm{10}{x}\:=\mathrm{13}\:\Leftrightarrow{x}=\frac{\mathrm{13}}{\mathrm{10}}\right.\right. \\ $$$$\frac{\mathrm{13}}{\mathrm{10}}\:−\frac{\mathrm{5}}{\mathrm{7}}\:=\frac{\mathrm{13}.\mathrm{7}\:−\mathrm{50}}{\mathrm{70}}>\mathrm{0}\:\Rightarrow\frac{\mathrm{13}}{\mathrm{10}}>\frac{\mathrm{5}}{\mathrm{7}}\:{so}\:{this}\:{number}\:{is}\:{solution}\:\:{so}\:{the}\:\left({e}\right)\:{have}\: \\ $$$$\mathrm{2}\:{solutions}\:−\frac{\mathrm{17}}{\mathrm{10}}\:{and}\:\frac{\mathrm{5}}{\mathrm{7}}\:. \\ $$$$\mid \\ $$
Commented by hassentimol last updated on 07/Nov/18
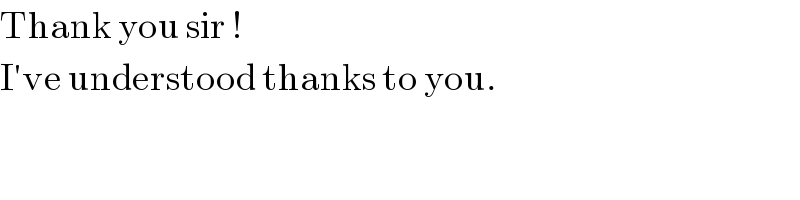
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}\:! \\ $$$$\mathrm{I}'\mathrm{ve}\:\mathrm{understood}\:\mathrm{thanks}\:\mathrm{to}\:\mathrm{you}. \\ $$
Commented by maxmathsup by imad last updated on 07/Nov/18

$${you}\:{are}\:{welcome}.. \\ $$
Answered by MJS last updated on 06/Nov/18
![x<−(2/3) ⇒ ∣3x+2∣=−3x−2 x≥−(2/3) ⇒ ∣3x+2∣=3x+2 x<(5/7) ⇒ ∣7x−5∣=5−7x x≥(5/7) ⇒ ∣7x−5∣=7x−5 x∈I_1 =]−∞; −(2/3)[ −3x−2+5−7x=20 ⇒ x=−((17)/(10)) x∈I_2 =[−(2/3);(5/7)[ 3x+2+5−7x=20 ⇒ x=−((13)/4)∉I_2 ⇒ no solution x∈I_3 =[(5/7); +∞[ 3x+2+7x−5=20 ⇒ x=((23)/(10))](Q47249.png)
$$ \\ $$$${x}<−\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\:\mid\mathrm{3}{x}+\mathrm{2}\mid=−\mathrm{3}{x}−\mathrm{2} \\ $$$${x}\geqslant−\frac{\mathrm{2}}{\mathrm{3}}\:\Rightarrow\:\mid\mathrm{3}{x}+\mathrm{2}\mid=\mathrm{3}{x}+\mathrm{2} \\ $$$${x}<\frac{\mathrm{5}}{\mathrm{7}}\:\Rightarrow\:\mid\mathrm{7}{x}−\mathrm{5}\mid=\mathrm{5}−\mathrm{7}{x}\:\: \\ $$$${x}\geqslant\frac{\mathrm{5}}{\mathrm{7}}\:\Rightarrow\:\mid\mathrm{7}{x}−\mathrm{5}\mid=\mathrm{7}{x}−\mathrm{5} \\ $$$$\left.{x}\in{I}_{\mathrm{1}} =\right]−\infty;\:−\frac{\mathrm{2}}{\mathrm{3}}\left[\right. \\ $$$$−\mathrm{3}{x}−\mathrm{2}+\mathrm{5}−\mathrm{7}{x}=\mathrm{20}\:\Rightarrow\:{x}=−\frac{\mathrm{17}}{\mathrm{10}} \\ $$$${x}\in{I}_{\mathrm{2}} =\left[−\frac{\mathrm{2}}{\mathrm{3}};\frac{\mathrm{5}}{\mathrm{7}}\left[\right.\right. \\ $$$$\mathrm{3}{x}+\mathrm{2}+\mathrm{5}−\mathrm{7}{x}=\mathrm{20}\:\Rightarrow\:{x}=−\frac{\mathrm{13}}{\mathrm{4}}\notin{I}_{\mathrm{2}} \:\Rightarrow\:\mathrm{no}\:\mathrm{solution} \\ $$$${x}\in{I}_{\mathrm{3}} =\left[\frac{\mathrm{5}}{\mathrm{7}};\:+\infty\left[\right.\right. \\ $$$$\mathrm{3}{x}+\mathrm{2}+\mathrm{7}{x}−\mathrm{5}=\mathrm{20}\:\Rightarrow\:{x}=\frac{\mathrm{23}}{\mathrm{10}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 07/Nov/18
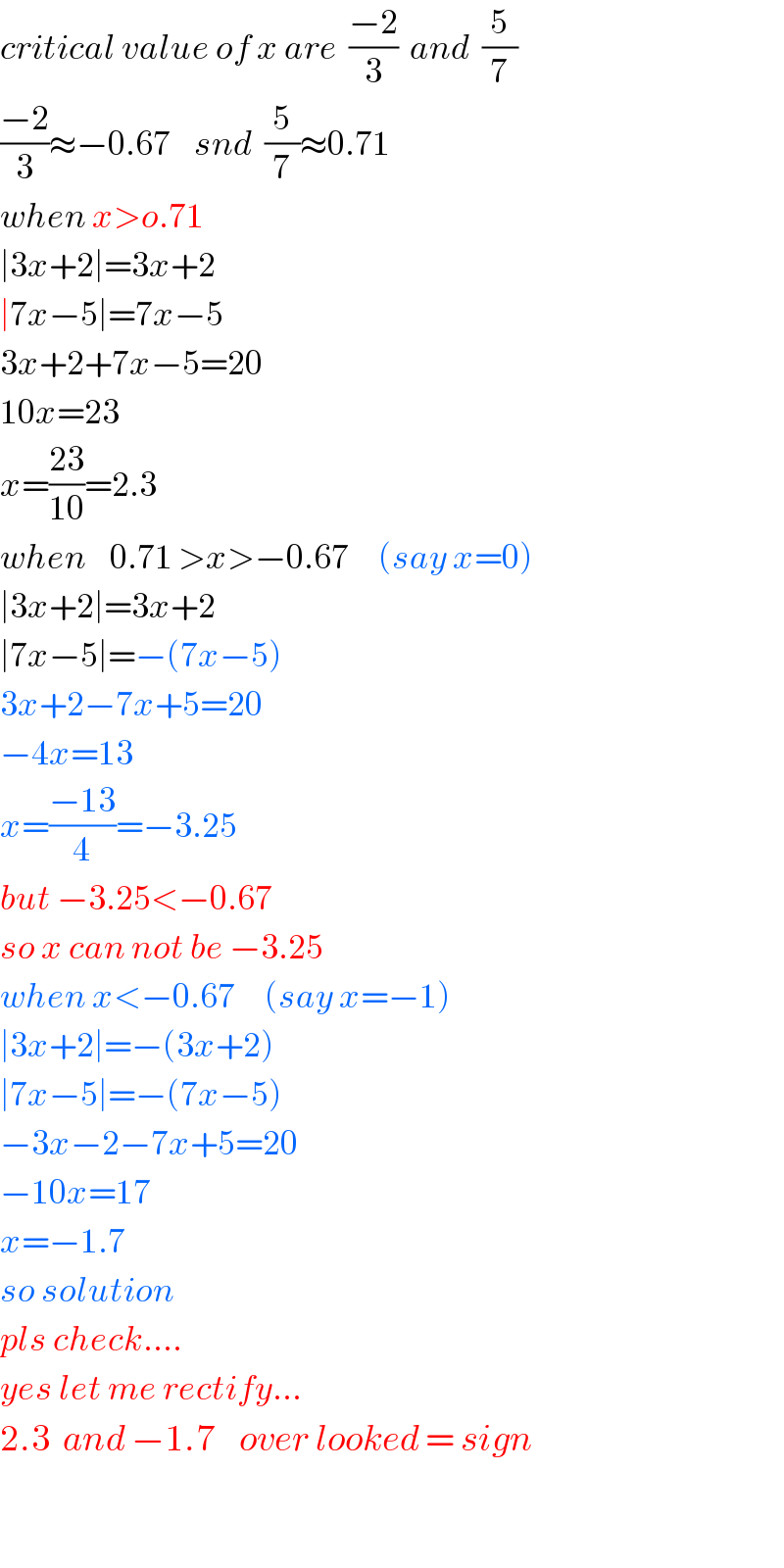
$${critical}\:{value}\:{of}\:{x}\:{are}\:\:\frac{−\mathrm{2}}{\mathrm{3}}\:\:{and}\:\:\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\frac{−\mathrm{2}}{\mathrm{3}}\approx−\mathrm{0}.\mathrm{67}\:\:\:\:{snd}\:\:\frac{\mathrm{5}}{\mathrm{7}}\approx\mathrm{0}.\mathrm{71} \\ $$$${when}\:{x}>{o}.\mathrm{71} \\ $$$$\mid\mathrm{3}{x}+\mathrm{2}\mid=\mathrm{3}{x}+\mathrm{2} \\ $$$$\mid\mathrm{7}{x}−\mathrm{5}\mid=\mathrm{7}{x}−\mathrm{5} \\ $$$$\mathrm{3}{x}+\mathrm{2}+\mathrm{7}{x}−\mathrm{5}=\mathrm{20} \\ $$$$\mathrm{10}{x}=\mathrm{23} \\ $$$${x}=\frac{\mathrm{23}}{\mathrm{10}}=\mathrm{2}.\mathrm{3} \\ $$$${when}\:\:\:\:\mathrm{0}.\mathrm{71}\:>{x}>−\mathrm{0}.\mathrm{67}\:\:\:\:\:\left({say}\:{x}=\mathrm{0}\right) \\ $$$$\mid\mathrm{3}{x}+\mathrm{2}\mid=\mathrm{3}{x}+\mathrm{2} \\ $$$$\mid\mathrm{7}{x}−\mathrm{5}\mid=−\left(\mathrm{7}{x}−\mathrm{5}\right) \\ $$$$\mathrm{3}{x}+\mathrm{2}−\mathrm{7}{x}+\mathrm{5}=\mathrm{20} \\ $$$$−\mathrm{4}{x}=\mathrm{13} \\ $$$${x}=\frac{−\mathrm{13}}{\mathrm{4}}=−\mathrm{3}.\mathrm{25} \\ $$$${but}\:−\mathrm{3}.\mathrm{25}<−\mathrm{0}.\mathrm{67} \\ $$$${so}\:{x}\:{can}\:{not}\:{be}\:−\mathrm{3}.\mathrm{25} \\ $$$${when}\:{x}<−\mathrm{0}.\mathrm{67}\:\:\:\:\:\left({say}\:{x}=−\mathrm{1}\right) \\ $$$$\mid\mathrm{3}{x}+\mathrm{2}\mid=−\left(\mathrm{3}{x}+\mathrm{2}\right) \\ $$$$\mid\mathrm{7}{x}−\mathrm{5}\mid=−\left(\mathrm{7}{x}−\mathrm{5}\right) \\ $$$$−\mathrm{3}{x}−\mathrm{2}−\mathrm{7}{x}+\mathrm{5}=\mathrm{20} \\ $$$$−\mathrm{10}{x}=\mathrm{17} \\ $$$${x}=−\mathrm{1}.\mathrm{7}\:\:\: \\ $$$${so}\:{solution}\: \\ $$$${pls}\:{check}.... \\ $$$${yes}\:{let}\:{me}\:{rectify}... \\ $$$$\mathrm{2}.\mathrm{3}\:\:{and}\:−\mathrm{1}.\mathrm{7}\:\:\:\:{over}\:{looked}\:=\:{sign} \\ $$$$ \\ $$
Commented by hassentimol last updated on 06/Nov/18

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}, \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 06/Nov/18

$${to}\:{make}\:{one}\:{understand}\:{is}\:{my}\:{gift}... \\ $$
Commented by hassentimol last updated on 06/Nov/18
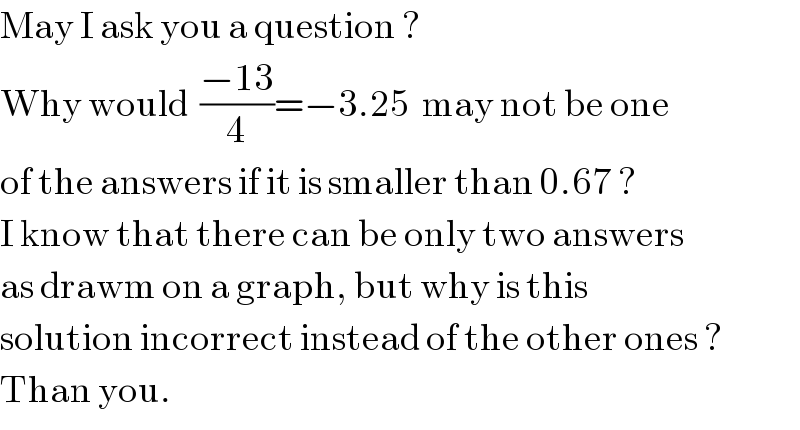
$$\mathrm{May}\:\mathrm{I}\:\mathrm{ask}\:\mathrm{you}\:\mathrm{a}\:\mathrm{question}\:? \\ $$$$\mathrm{Why}\:\mathrm{would}\:\:\frac{−\mathrm{13}}{\mathrm{4}}=−\mathrm{3}.\mathrm{25}\:\:\mathrm{may}\:\mathrm{not}\:\mathrm{be}\:\mathrm{one} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{answers}\:\mathrm{if}\:\mathrm{it}\:\mathrm{is}\:\mathrm{smaller}\:\mathrm{than}\:\mathrm{0}.\mathrm{67}\:? \\ $$$$\mathrm{I}\:\mathrm{know}\:\mathrm{that}\:\mathrm{there}\:\mathrm{can}\:\mathrm{be}\:\mathrm{only}\:\mathrm{two}\:\mathrm{answers} \\ $$$$\mathrm{as}\:\mathrm{drawm}\:\mathrm{on}\:\mathrm{a}\:\mathrm{graph},\:\mathrm{but}\:\mathrm{why}\:\mathrm{is}\:\mathrm{this} \\ $$$$\mathrm{solution}\:\mathrm{incorrect}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{the}\:\mathrm{other}\:\mathrm{ones}\:? \\ $$$$\mathrm{Than}\:\mathrm{you}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 07/Nov/18

$${thank}\:{you}\:{sir}... \\ $$
Answered by peter frank last updated on 07/Nov/18
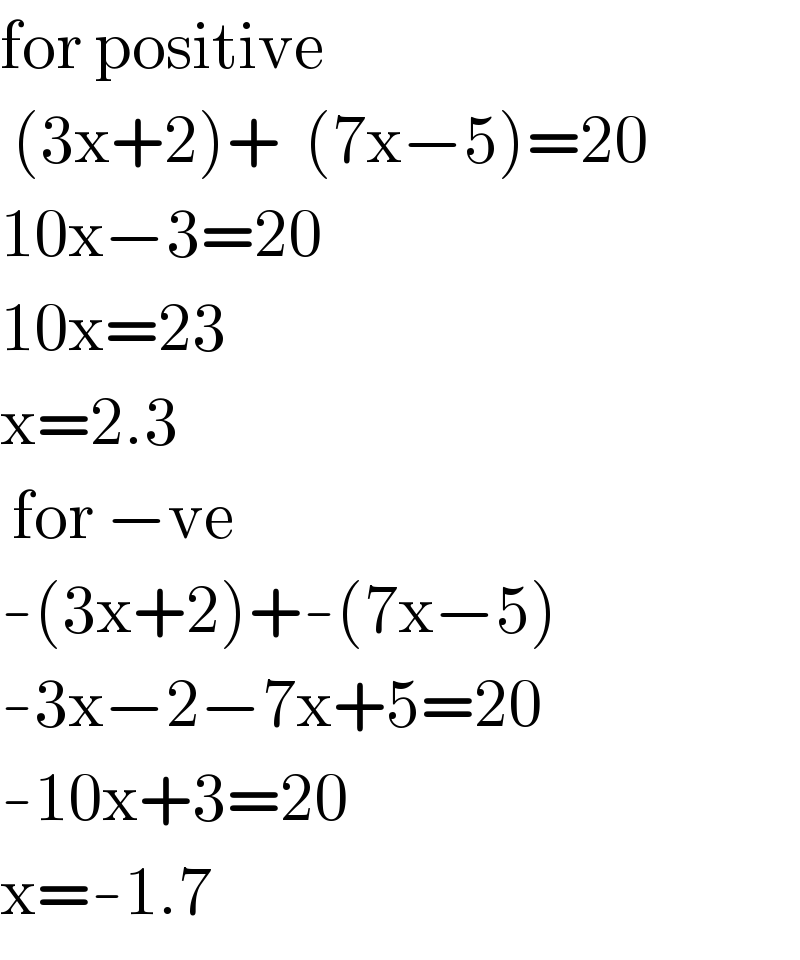
$$\mathrm{for}\:\mathrm{positive} \\ $$$$\:\left(\mathrm{3x}+\mathrm{2}\right)+\:\:\left(\mathrm{7x}−\mathrm{5}\right)=\mathrm{20} \\ $$$$\mathrm{10x}−\mathrm{3}=\mathrm{20} \\ $$$$\mathrm{10x}=\mathrm{23} \\ $$$$\mathrm{x}=\mathrm{2}.\mathrm{3} \\ $$$$\:\mathrm{for}\:−\mathrm{ve} \\ $$$$-\left(\mathrm{3x}+\mathrm{2}\right)+-\left(\mathrm{7x}−\mathrm{5}\right) \\ $$$$-\mathrm{3x}−\mathrm{2}−\mathrm{7x}+\mathrm{5}=\mathrm{20} \\ $$$$-\mathrm{10x}+\mathrm{3}=\mathrm{20} \\ $$$$\mathrm{x}=-\mathrm{1}.\mathrm{7} \\ $$
Commented by maxmathsup by imad last updated on 06/Nov/18
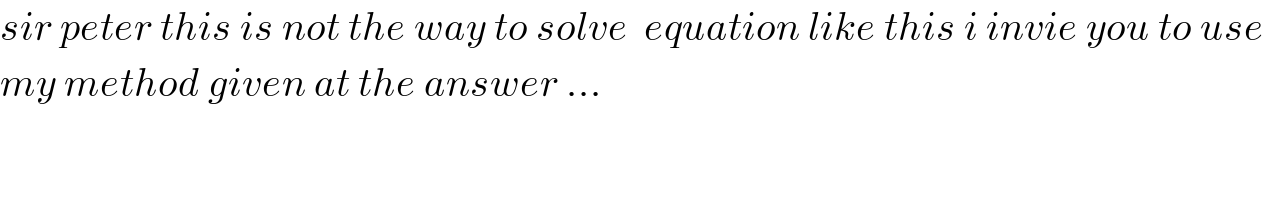
$${sir}\:{peter}\:{this}\:{is}\:{not}\:{the}\:{way}\:{to}\:{solve}\:\:{equation}\:{like}\:{this}\:{i}\:{invie}\:{you}\:{to}\:{use}\: \\ $$$${my}\:{method}\:{given}\:{at}\:{the}\:{answer}\:... \\ $$
