Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 205324 by hardmath last updated on 16/Mar/24

Compare: 37^(37) and 36^(38)

$$\mathrm{Compare}: \\ $$$$\mathrm{37}^{\mathrm{37}} \:\:\:\mathrm{and}\:\:\:\mathrm{36}^{\mathrm{38}} \\ $$

Answered by nikif99 last updated on 16/Mar/24

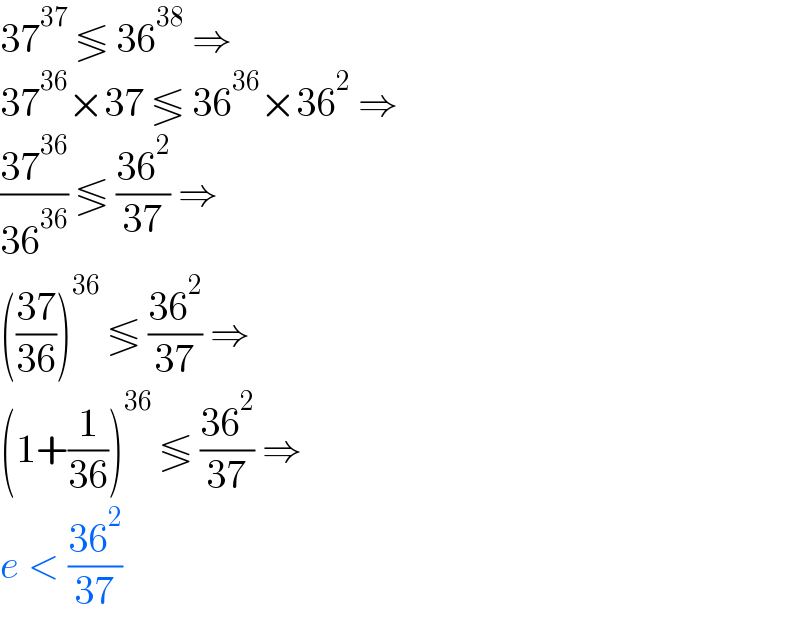
37^(37) ≶ 36^(38) ⇒ 37^(36) ×37 ≶ 36^(36) ×36^2 ⇒ ((37^(36) )/(36^(36) )) ≶ ((36^2 )/(37)) ⇒ (((37)/(36)))^(36) ≶ ((36^2 )/(37)) ⇒ (1+(1/(36)))^(36) ≶ ((36^2 )/(37)) ⇒ e < ((36^2 )/(37))

$$\mathrm{37}^{\mathrm{37}} \:\lessgtr\:\mathrm{36}^{\mathrm{38}} \:\Rightarrow \\ $$$$\mathrm{37}^{\mathrm{36}} ×\mathrm{37}\:\lessgtr\:\mathrm{36}^{\mathrm{36}} ×\mathrm{36}^{\mathrm{2}} \:\Rightarrow \\ $$$$\frac{\mathrm{37}^{\mathrm{36}} }{\mathrm{36}^{\mathrm{36}} }\:\lessgtr\:\frac{\mathrm{36}^{\mathrm{2}} }{\mathrm{37}}\:\Rightarrow \\ $$$$\left(\frac{\mathrm{37}}{\mathrm{36}}\right)^{\mathrm{36}} \:\lessgtr\:\frac{\mathrm{36}^{\mathrm{2}} }{\mathrm{37}}\:\Rightarrow \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{36}}\right)^{\mathrm{36}} \:\lessgtr\:\frac{\mathrm{36}^{\mathrm{2}} }{\mathrm{37}}\:\Rightarrow \\ $$$${e}\:<\:\frac{\mathrm{36}^{\mathrm{2}} }{\mathrm{37}} \\ $$

Answered by Frix last updated on 16/Mar/24

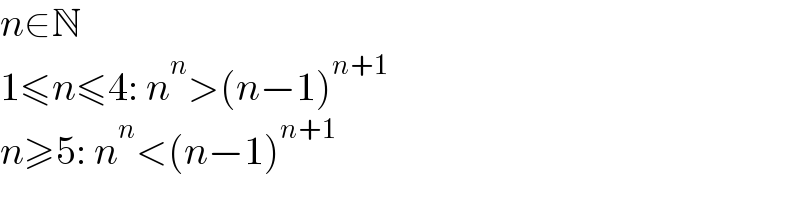
n∈N 1≤n≤4: n^n >(n−1)^(n+1) n≥5: n^n <(n−1)^(n+1)

$${n}\in\mathbb{N} \\ $$$$\mathrm{1}\leqslant{n}\leqslant\mathrm{4}:\:{n}^{{n}} >\left({n}−\mathrm{1}\right)^{{n}+\mathrm{1}} \\ $$$${n}\geqslant\mathrm{5}:\:{n}^{{n}} <\left({n}−\mathrm{1}\right)^{{n}+\mathrm{1}} \\ $$

Answered by Berbere last updated on 17/Mar/24

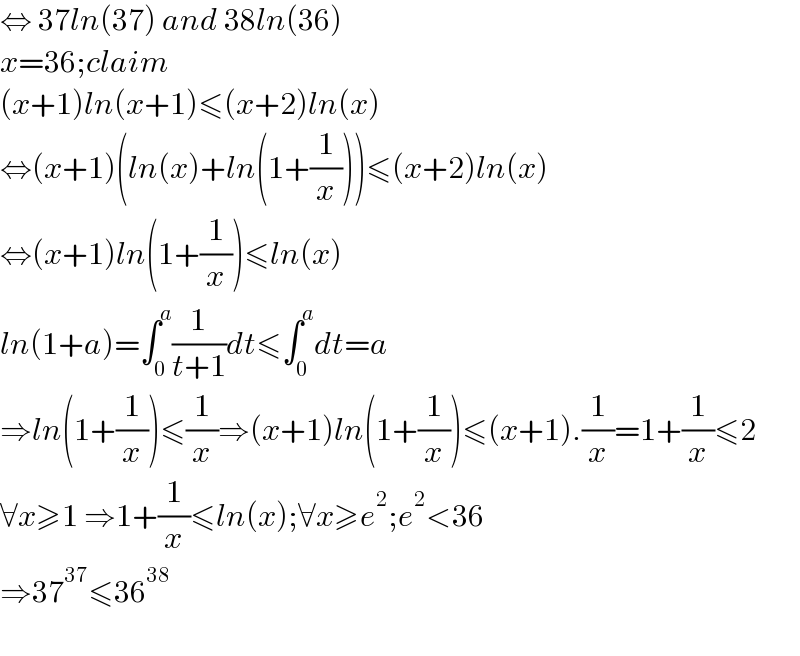
⇔ 37ln(37) and 38ln(36) x=36;claim (x+1)ln(x+1)≤(x+2)ln(x) ⇔(x+1)(ln(x)+ln(1+(1/x)))≤(x+2)ln(x) ⇔(x+1)ln(1+(1/x))≤ln(x) ln(1+a)=∫_0 ^a (1/(t+1))dt≤∫_0 ^a dt=a ⇒ln(1+(1/x))≤(1/x)⇒(x+1)ln(1+(1/x))≤(x+1).(1/x)=1+(1/x)≤2 ∀x≥1 ⇒1+(1/x)≤ln(x);∀x≥e^2 ;e^2 <36 ⇒37^(37) ≤36^(38)

$$\Leftrightarrow\:\mathrm{37}{ln}\left(\mathrm{37}\right)\:{and}\:\mathrm{38}{ln}\left(\mathrm{36}\right) \\ $$$${x}=\mathrm{36};{claim} \\ $$$$\left({x}+\mathrm{1}\right){ln}\left({x}+\mathrm{1}\right)\leqslant\left({x}+\mathrm{2}\right){ln}\left({x}\right) \\ $$$$\Leftrightarrow\left({x}+\mathrm{1}\right)\left({ln}\left({x}\right)+{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\right)\leqslant\left({x}+\mathrm{2}\right){ln}\left({x}\right) \\ $$$$\Leftrightarrow\left({x}+\mathrm{1}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\leqslant{ln}\left({x}\right) \\ $$$${ln}\left(\mathrm{1}+{a}\right)=\int_{\mathrm{0}} ^{{a}} \frac{\mathrm{1}}{{t}+\mathrm{1}}{dt}\leqslant\int_{\mathrm{0}} ^{{a}} {dt}={a} \\ $$$$\Rightarrow{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\leqslant\frac{\mathrm{1}}{{x}}\Rightarrow\left({x}+\mathrm{1}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)\leqslant\left({x}+\mathrm{1}\right).\frac{\mathrm{1}}{{x}}=\mathrm{1}+\frac{\mathrm{1}}{{x}}\leqslant\mathrm{2} \\ $$$$\forall{x}\geqslant\mathrm{1}\:\Rightarrow\mathrm{1}+\frac{\mathrm{1}}{{x}}\leqslant{ln}\left({x}\right);\forall{x}\geqslant{e}^{\mathrm{2}} ;{e}^{\mathrm{2}} <\mathrm{36} \\ $$$$\Rightarrow\mathrm{37}^{\mathrm{37}} \leqslant\mathrm{36}^{\mathrm{38}} \\ $$$$ \\ $$

Commented by hardmath last updated on 18/Mar/24

cool dear professors thank you

$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professors}\:\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com