
Question Number 48443 by rahul 19 last updated on 24/Nov/18
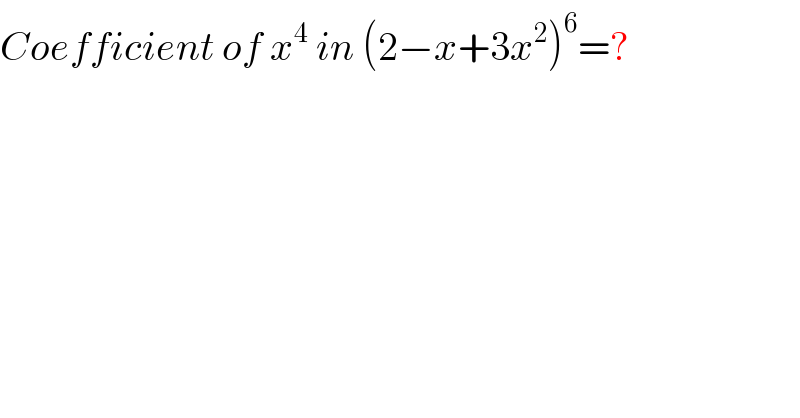
$${Coefficient}\:{of}\:{x}^{\mathrm{4}} \:{in}\:\left(\mathrm{2}−{x}+\mathrm{3}{x}^{\mathrm{2}} \right)^{\mathrm{6}} =? \\ $$
Commented by rahul 19 last updated on 24/Nov/18
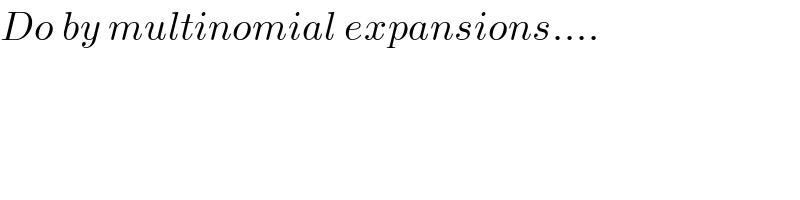
$${Do}\:{by}\:{multinomial}\:{expansions}.... \\ $$
Commented by Meritguide1234 last updated on 24/Nov/18
$${rahul}\:{your}\:{post}\:{are}\:{nice}\:{post}\:{more}\:{questions}\:{like}\:{this} \\ $$
Commented by rahul 19 last updated on 24/Nov/18
$${Sure}\:{sir}! \\ $$$${I}'{ll}\:{post}\:{tomorrow}... \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 24/Nov/18
![((6!)/(a!b!c!))(2)^a (−x)^b (3x^2 )^c =((6!)/(a!b!c!))(2)^a (3)^c (−1)^b (x)^(b+2c) a+b+c=6 b+2c=4 b=0 c=2 so a=4 b=2 c=1 a=3 b=4 c=0 a=2 so required coefficient is [((6!)/(4!0!2!))×(2)^4 (3)^2 (−1)^0 +((6!)/(3!2!1!))×(2)^3 (3)^1 (−1)^2 + ((6!)/(2!4!0!))×(2)^2 (3)^0 (−1)^4 ] pls check and calculate... [15×16×9+60×8×3+15×4 = 2160 +1440+60 =3660](Q48445.png)
$$\frac{\mathrm{6}!}{{a}!{b}!{c}!}\left(\mathrm{2}\right)^{{a}} \left(−{x}\right)^{{b}} \left(\mathrm{3}{x}^{\mathrm{2}} \right)^{{c}} \\ $$$$=\frac{\mathrm{6}!}{{a}!{b}!{c}!}\left(\mathrm{2}\right)^{{a}} \left(\mathrm{3}\right)^{{c}} \left(−\mathrm{1}\right)^{{b}} \left({x}\right)^{{b}+\mathrm{2}{c}} \\ $$$${a}+{b}+{c}=\mathrm{6} \\ $$$${b}+\mathrm{2}{c}=\mathrm{4} \\ $$$${b}=\mathrm{0}\:\:\:{c}=\mathrm{2}\:\:{so}\:{a}=\mathrm{4} \\ $$$${b}=\mathrm{2}\:\:\:{c}=\mathrm{1}\:\:\:\:{a}=\mathrm{3} \\ $$$${b}=\mathrm{4}\:\:\:\:{c}=\mathrm{0}\:\:\:\:{a}=\mathrm{2} \\ $$$${so}\:{required}\:{coefficient}\:{is} \\ $$$$\left[\frac{\mathrm{6}!}{\mathrm{4}!\mathrm{0}!\mathrm{2}!}×\left(\mathrm{2}\right)^{\mathrm{4}} \left(\mathrm{3}\right)^{\mathrm{2}} \left(−\mathrm{1}\right)^{\mathrm{0}} +\frac{\mathrm{6}!}{\mathrm{3}!\mathrm{2}!\mathrm{1}!}×\left(\mathrm{2}\right)^{\mathrm{3}} \left(\mathrm{3}\right)^{\mathrm{1}} \left(−\mathrm{1}\right)^{\mathrm{2}} +\right. \\ $$$$ \\ $$$$\left.\frac{\mathrm{6}!}{\mathrm{2}!\mathrm{4}!\mathrm{0}!}×\left(\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{3}\right)^{\mathrm{0}} \left(−\mathrm{1}\right)^{\mathrm{4}} \right] \\ $$$$\:{pls}\:{check}\:{and}\:{calculate}... \\ $$$$\left[\mathrm{15}×\mathrm{16}×\mathrm{9}+\mathrm{60}×\mathrm{8}×\mathrm{3}+\mathrm{15}×\mathrm{4}\right. \\ $$$$=\:\:\:\:\:\:\mathrm{2160}\:\:\:\:\:+\mathrm{1440}+\mathrm{60} \\ $$$$=\mathrm{3660} \\ $$
Commented by rahul 19 last updated on 24/Nov/18
=3660. (2160+1440+60)...I forgot the last case! thanks sir ����
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Nov/18

$${thank}\:{you}\:{for}\:{recheck}\:{in}\:{calculation} \\ $$$${i}\:{have}\:{used}\:\mathrm{3}!\:{twice}\:{by}\:{mistake}... \\ $$
