Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 195129 by a.lgnaoui last updated on 25/Jul/23

Calculer la valeur de la serie suivante: S=(3/2)+(5/8)+(7/(32))+(9/(128))+.....

$$\mathrm{Calculer}\:\mathrm{la}\:\mathrm{valeur}\:\mathrm{de}\:\mathrm{la}\:\mathrm{serie}\:\mathrm{suivante}: \\ $$$$\boldsymbol{\mathrm{S}}=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{32}}+\frac{\mathrm{9}}{\mathrm{128}}+..... \\ $$

Answered by MM42 last updated on 25/Jul/23

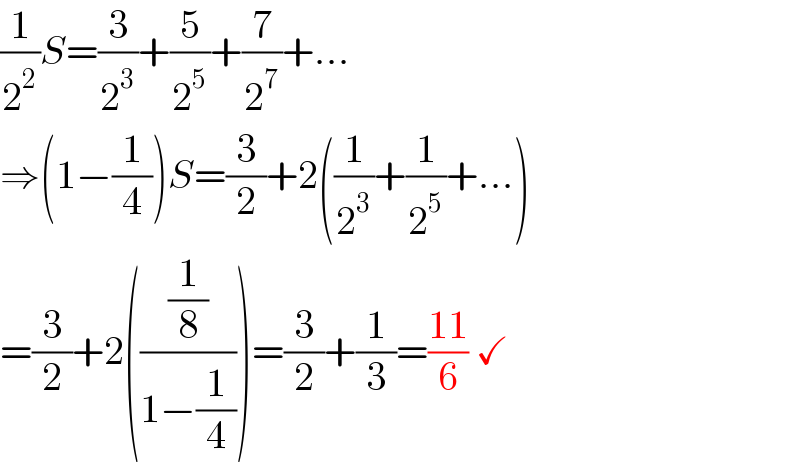
(1/2^2 )S=(3/2^3 )+(5/2^5 )+(7/2^7 )+... ⇒(1−(1/4))S=(3/2)+2((1/2^3 )+(1/2^5 )+...) =(3/2)+2(((1/8)/(1−(1/4))))=(3/2)+(1/3)=((11)/6) ✓

$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }{S}=\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{5}} }+\frac{\mathrm{7}}{\mathrm{2}^{\mathrm{7}} }+... \\ $$$$\Rightarrow\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right){S}=\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{5}} }+...\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{2}\left(\frac{\frac{\mathrm{1}}{\mathrm{8}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}\right)=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{11}}{\mathrm{6}}\:\checkmark \\ $$

Commented by a.lgnaoui last updated on 25/Jul/23

thanks

$$\mathrm{thanks} \\ $$

Commented by a.lgnaoui last updated on 25/Jul/23

but the answer is wrong

$$\mathrm{but}\:\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{wrong} \\ $$

Commented by MM42 last updated on 25/Jul/23

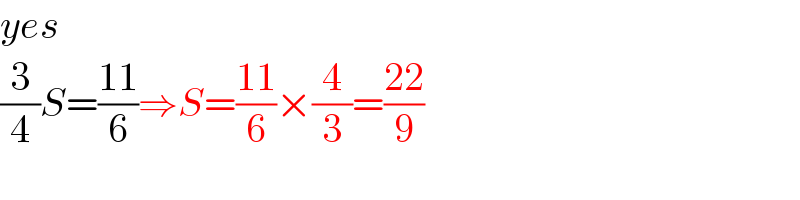
yes (3/4)S=((11)/6)⇒S=((11)/6)×(4/3)=((22)/9)

$${yes} \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}{S}=\frac{\mathrm{11}}{\mathrm{6}}\Rightarrow{S}=\frac{\mathrm{11}}{\mathrm{6}}×\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{22}}{\mathrm{9}} \\ $$

Answered by BaliramKumar last updated on 25/Jul/23

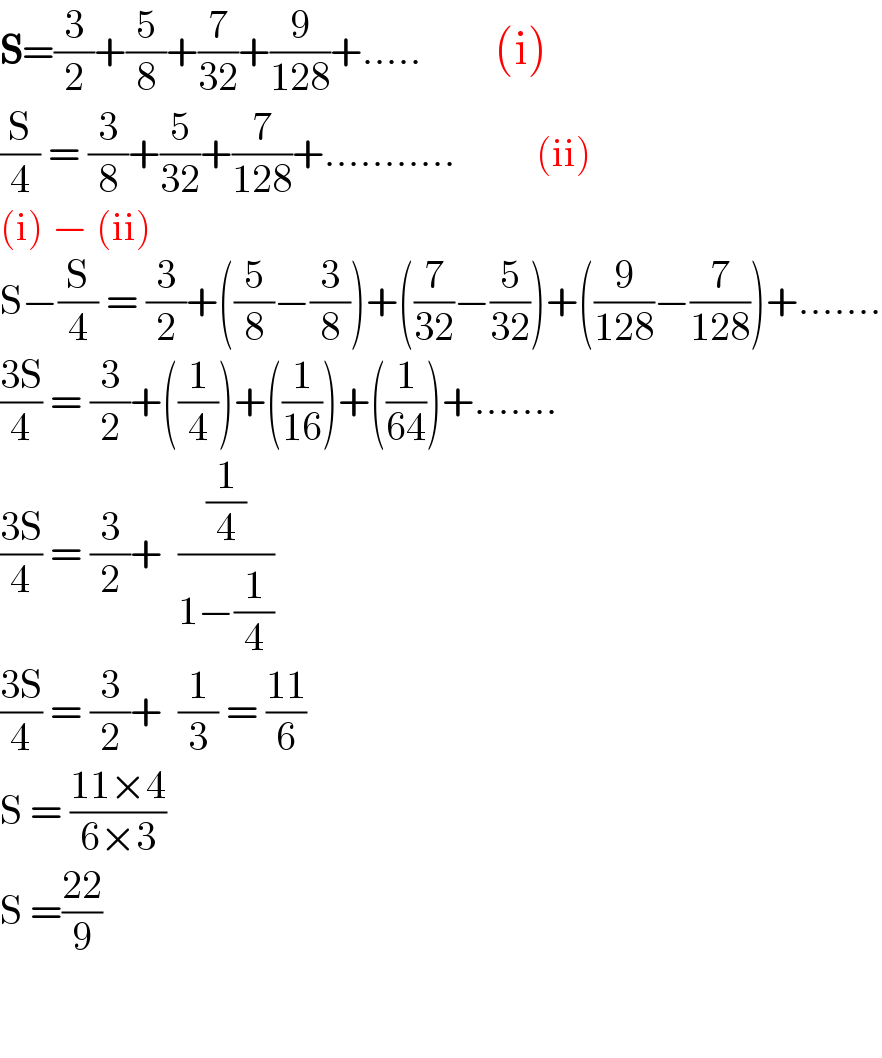
S=(3/2)+(5/8)+(7/(32))+(9/(128))+..... (i) (S/4) = (3/8)+(5/(32))+(7/(128))+........... (ii) (i) − (ii) S−(S/4) = (3/2)+((5/8)−(3/8))+((7/(32))−(5/(32)))+((9/(128))−(7/(128)))+....... ((3S)/4) = (3/2)+((1/4))+((1/(16)))+((1/(64)))+....... ((3S)/4) = (3/2)+ ((1/4)/(1−(1/4))) ((3S)/4) = (3/2)+ (1/3) = ((11)/6) S = ((11×4)/(6×3)) S =((22)/9)

$$\boldsymbol{\mathrm{S}}=\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{32}}+\frac{\mathrm{9}}{\mathrm{128}}+.....\:\:\:\:\:\:\:\:\:\left(\mathrm{i}\right) \\ $$$$\frac{\mathrm{S}}{\mathrm{4}}\:=\:\frac{\mathrm{3}}{\mathrm{8}}+\frac{\mathrm{5}}{\mathrm{32}}+\frac{\mathrm{7}}{\mathrm{128}}+...........\:\:\:\:\:\:\:\:\:\:\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)\:−\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{S}−\frac{\mathrm{S}}{\mathrm{4}}\:=\:\frac{\mathrm{3}}{\mathrm{2}}+\left(\frac{\mathrm{5}}{\mathrm{8}}−\frac{\mathrm{3}}{\mathrm{8}}\right)+\left(\frac{\mathrm{7}}{\mathrm{32}}−\frac{\mathrm{5}}{\mathrm{32}}\right)+\left(\frac{\mathrm{9}}{\mathrm{128}}−\frac{\mathrm{7}}{\mathrm{128}}\right)+....... \\ $$$$\frac{\mathrm{3S}}{\mathrm{4}}\:=\:\frac{\mathrm{3}}{\mathrm{2}}+\left(\frac{\mathrm{1}}{\mathrm{4}}\right)+\left(\frac{\mathrm{1}}{\mathrm{16}}\right)+\left(\frac{\mathrm{1}}{\mathrm{64}}\right)+....... \\ $$$$\frac{\mathrm{3S}}{\mathrm{4}}\:=\:\frac{\mathrm{3}}{\mathrm{2}}+\:\:\frac{\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\frac{\mathrm{3S}}{\mathrm{4}}\:=\:\frac{\mathrm{3}}{\mathrm{2}}+\:\:\frac{\mathrm{1}}{\mathrm{3}}\:=\:\frac{\mathrm{11}}{\mathrm{6}} \\ $$$$\mathrm{S}\:=\:\frac{\mathrm{11}×\mathrm{4}}{\mathrm{6}×\mathrm{3}} \\ $$$$\mathrm{S}\:=\frac{\mathrm{22}}{\mathrm{9}} \\ $$$$ \\ $$$$ \\ $$

Commented by a.lgnaoui last updated on 25/Jul/23

Exact ,thanks

$$\mathrm{Exact}\:,\mathrm{thanks} \\ $$

Answered by a.lgnaoui last updated on 25/Jul/23

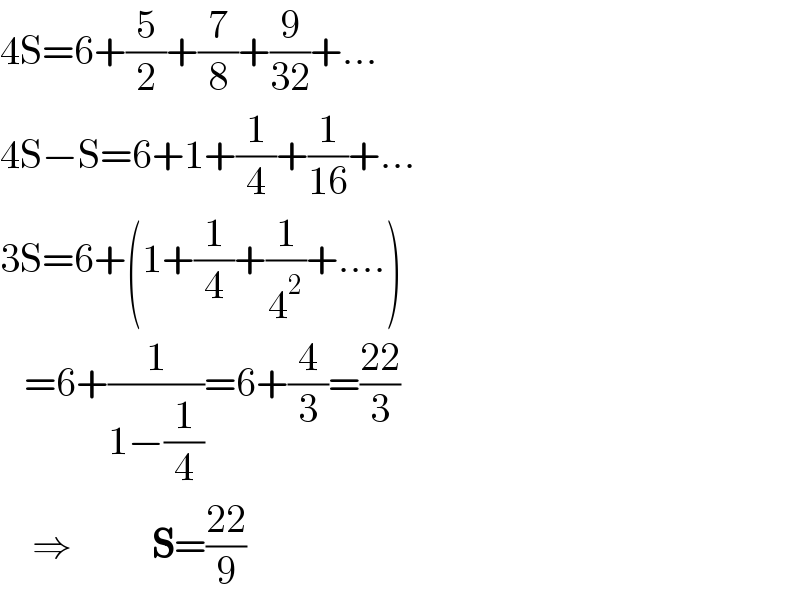
4S=6+(5/2)+(7/8)+(9/(32))+... 4S−S=6+1+(1/4)+(1/(16))+... 3S=6+(1+(1/4)+(1/4^2 )+....) =6+(1/(1−(1/4)))=6+(4/3)=((22)/3) ⇒ S=((22)/9)

$$\mathrm{4S}=\mathrm{6}+\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{7}}{\mathrm{8}}+\frac{\mathrm{9}}{\mathrm{32}}+... \\ $$$$\mathrm{4S}−\mathrm{S}=\mathrm{6}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{16}}+... \\ $$$$\mathrm{3S}=\mathrm{6}+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }+....\right) \\ $$$$\:\:\:=\mathrm{6}+\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}=\mathrm{6}+\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{22}}{\mathrm{3}} \\ $$$$\:\:\:\:\Rightarrow\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{S}}=\frac{\mathrm{22}}{\mathrm{9}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com