Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 196145 by Erico last updated on 18/Aug/23

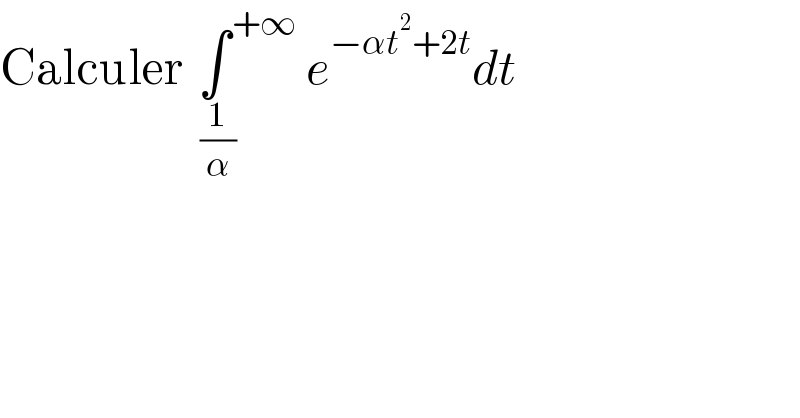
Calculer ∫^( +∞) _( (1/α)) e^(−αt^2 +2t) dt

$$\mathrm{Calculer}\:\underset{\:\frac{\mathrm{1}}{\alpha}} {\int}^{\:+\infty} {e}^{−\alpha{t}^{\mathrm{2}} +\mathrm{2}{t}} {dt} \\ $$

Answered by Mathspace last updated on 20/Aug/23

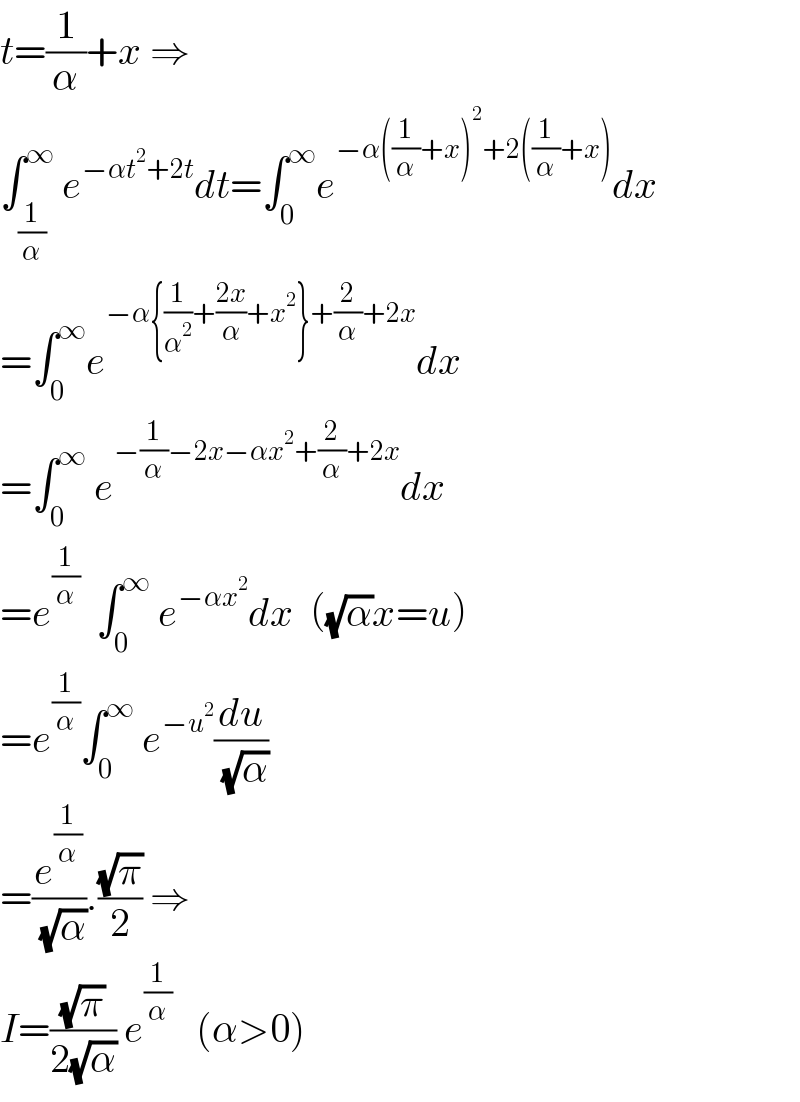
t=(1/α)+x ⇒ ∫_(1/α) ^∞ e^(−αt^2 +2t) dt=∫_0 ^∞ e^(−α((1/α)+x)^2 +2((1/α)+x)) dx =∫_0 ^∞ e^(−α{(1/α^2 )+((2x)/α)+x^2 }+(2/α)+2x) dx =∫_0 ^∞ e^(−(1/α)−2x−αx^2 +(2/α)+2x) dx =e^(1/α) ∫_0 ^∞ e^(−αx^2 ) dx ((√α)x=u) =e^(1/α) ∫_0 ^∞ e^(−u^2 ) (du/( (√α))) =(e^(1/α) /( (√α))).((√π)/2) ⇒ I=((√π)/(2(√α))) e^(1/α) (α>0)

$${t}=\frac{\mathrm{1}}{\alpha}+{x}\:\Rightarrow \\ $$$$\int_{\frac{\mathrm{1}}{\alpha}} ^{\infty} \:{e}^{−\alpha{t}^{\mathrm{2}} +\mathrm{2}{t}} {dt}=\int_{\mathrm{0}} ^{\infty} {e}^{−\alpha\left(\frac{\mathrm{1}}{\alpha}+{x}\right)^{\mathrm{2}} +\mathrm{2}\left(\frac{\mathrm{1}}{\alpha}+{x}\right)} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\alpha\left\{\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }+\frac{\mathrm{2}{x}}{\alpha}+{x}^{\mathrm{2}} \right\}+\frac{\mathrm{2}}{\alpha}+\mathrm{2}{x}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\frac{\mathrm{1}}{\alpha}−\mathrm{2}{x}−\alpha{x}^{\mathrm{2}} +\frac{\mathrm{2}}{\alpha}+\mathrm{2}{x}} {dx} \\ $$$$={e}^{\frac{\mathrm{1}}{\alpha}} \:\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\alpha{x}^{\mathrm{2}} } {dx}\:\:\left(\sqrt{\alpha}{x}={u}\right) \\ $$$$={e}^{\frac{\mathrm{1}}{\alpha}} \int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}^{\mathrm{2}} } \frac{{du}}{\:\sqrt{\alpha}} \\ $$$$=\frac{{e}^{\frac{\mathrm{1}}{\alpha}} }{\:\sqrt{\alpha}}.\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow \\ $$$${I}=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\alpha}}\:{e}^{\frac{\mathrm{1}}{\alpha}} \:\:\:\left(\alpha>\mathrm{0}\right) \\ $$

Commented by Mathspace last updated on 20/Aug/23

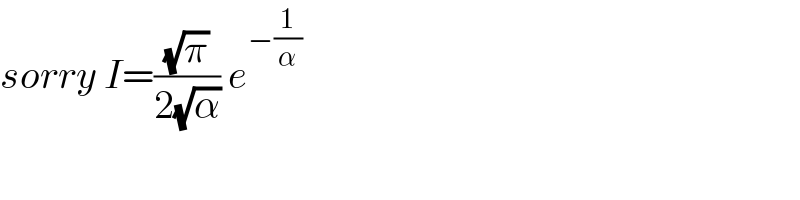
sorry I=((√π)/(2(√α))) e^(−(1/α))

$${sorry}\:{I}=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\alpha}}\:{e}^{−\frac{\mathrm{1}}{\alpha}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com