Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 72362 by Maclaurin Stickker last updated on 27/Oct/19

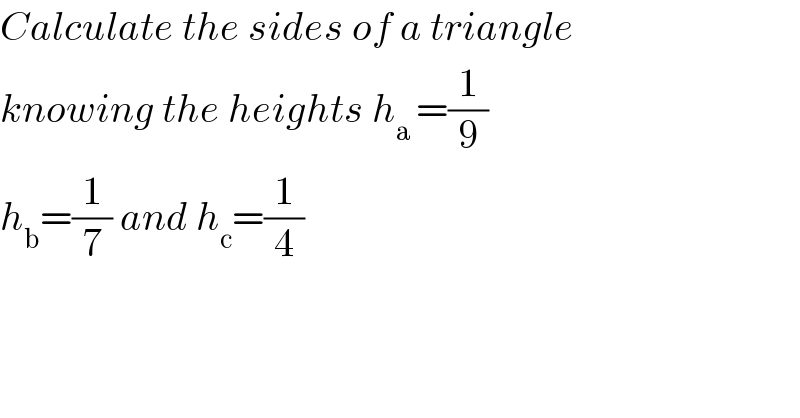
Calculate the sides of a triangle knowing the heights h_(a ) =(1/9) h_b =(1/7) and h_c =(1/4)

$${Calculate}\:{the}\:{sides}\:{of}\:{a}\:{triangle} \\ $$$${knowing}\:{the}\:{heights}\:{h}_{\mathrm{a}\:} =\frac{\mathrm{1}}{\mathrm{9}} \\ $$$${h}_{\mathrm{b}} =\frac{\mathrm{1}}{\mathrm{7}}\:{and}\:{h}_{\mathrm{c}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Answered by mr W last updated on 27/Oct/19

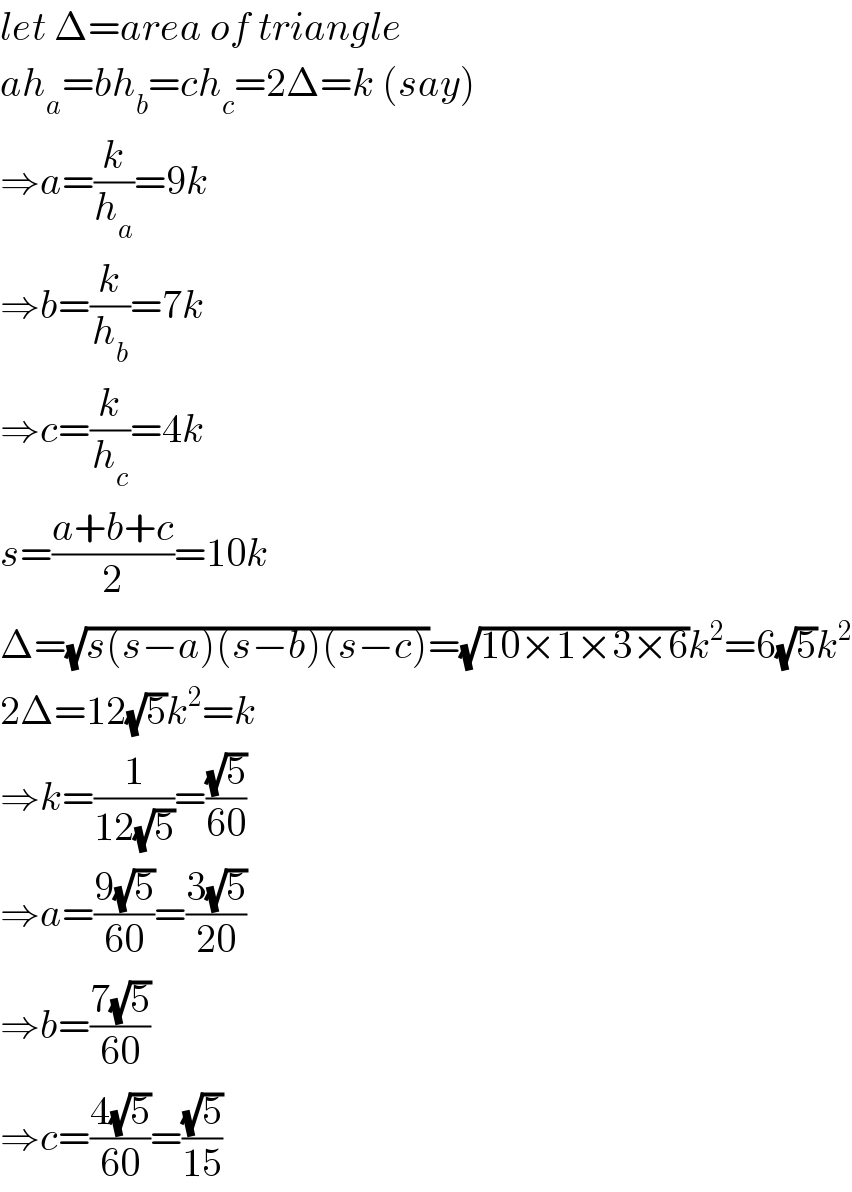
let Δ=area of triangle ah_a =bh_b =ch_c =2Δ=k (say) ⇒a=(k/h_a )=9k ⇒b=(k/h_b )=7k ⇒c=(k/h_c )=4k s=((a+b+c)/2)=10k Δ=(√(s(s−a)(s−b)(s−c)))=(√(10×1×3×6))k^2 =6(√5)k^2 2Δ=12(√5)k^2 =k ⇒k=(1/(12(√5)))=((√5)/(60)) ⇒a=((9(√5))/(60))=((3(√5))/(20)) ⇒b=((7(√5))/(60)) ⇒c=((4(√5))/(60))=((√5)/(15))

$${let}\:\Delta={area}\:{of}\:{triangle} \\ $$$${ah}_{{a}} ={bh}_{{b}} ={ch}_{{c}} =\mathrm{2}\Delta={k}\:\left({say}\right) \\ $$$$\Rightarrow{a}=\frac{{k}}{{h}_{{a}} }=\mathrm{9}{k} \\ $$$$\Rightarrow{b}=\frac{{k}}{{h}_{{b}} }=\mathrm{7}{k} \\ $$$$\Rightarrow{c}=\frac{{k}}{{h}_{{c}} }=\mathrm{4}{k} \\ $$$${s}=\frac{{a}+{b}+{c}}{\mathrm{2}}=\mathrm{10}{k} \\ $$$$\Delta=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)}=\sqrt{\mathrm{10}×\mathrm{1}×\mathrm{3}×\mathrm{6}}{k}^{\mathrm{2}} =\mathrm{6}\sqrt{\mathrm{5}}{k}^{\mathrm{2}} \\ $$$$\mathrm{2}\Delta=\mathrm{12}\sqrt{\mathrm{5}}{k}^{\mathrm{2}} ={k} \\ $$$$\Rightarrow{k}=\frac{\mathrm{1}}{\mathrm{12}\sqrt{\mathrm{5}}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{60}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{9}\sqrt{\mathrm{5}}}{\mathrm{60}}=\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{20}} \\ $$$$\Rightarrow{b}=\frac{\mathrm{7}\sqrt{\mathrm{5}}}{\mathrm{60}} \\ $$$$\Rightarrow{c}=\frac{\mathrm{4}\sqrt{\mathrm{5}}}{\mathrm{60}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{15}} \\ $$

Commented by Maclaurin Stickker last updated on 27/Oct/19

Why a=9k?

$${Why}\:{a}=\mathrm{9}{k}? \\ $$

Commented by mr W last updated on 27/Oct/19

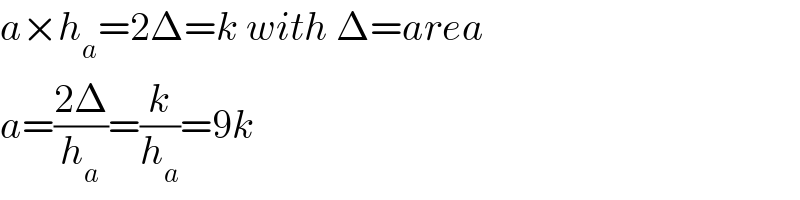
a×h_a =2Δ=k with Δ=area a=((2Δ)/h_a )=(k/h_a )=9k

$${a}×{h}_{{a}} =\mathrm{2}\Delta={k}\:{with}\:\Delta={area} \\ $$$${a}=\frac{\mathrm{2}\Delta}{{h}_{{a}} }=\frac{{k}}{{h}_{{a}} }=\mathrm{9}{k} \\ $$

Commented by Maclaurin Stickker last updated on 27/Oct/19

Oh, thank you.

$${Oh},\:{thank}\:{you}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com