
Question Number 207106 by Wuji last updated on 07/May/24
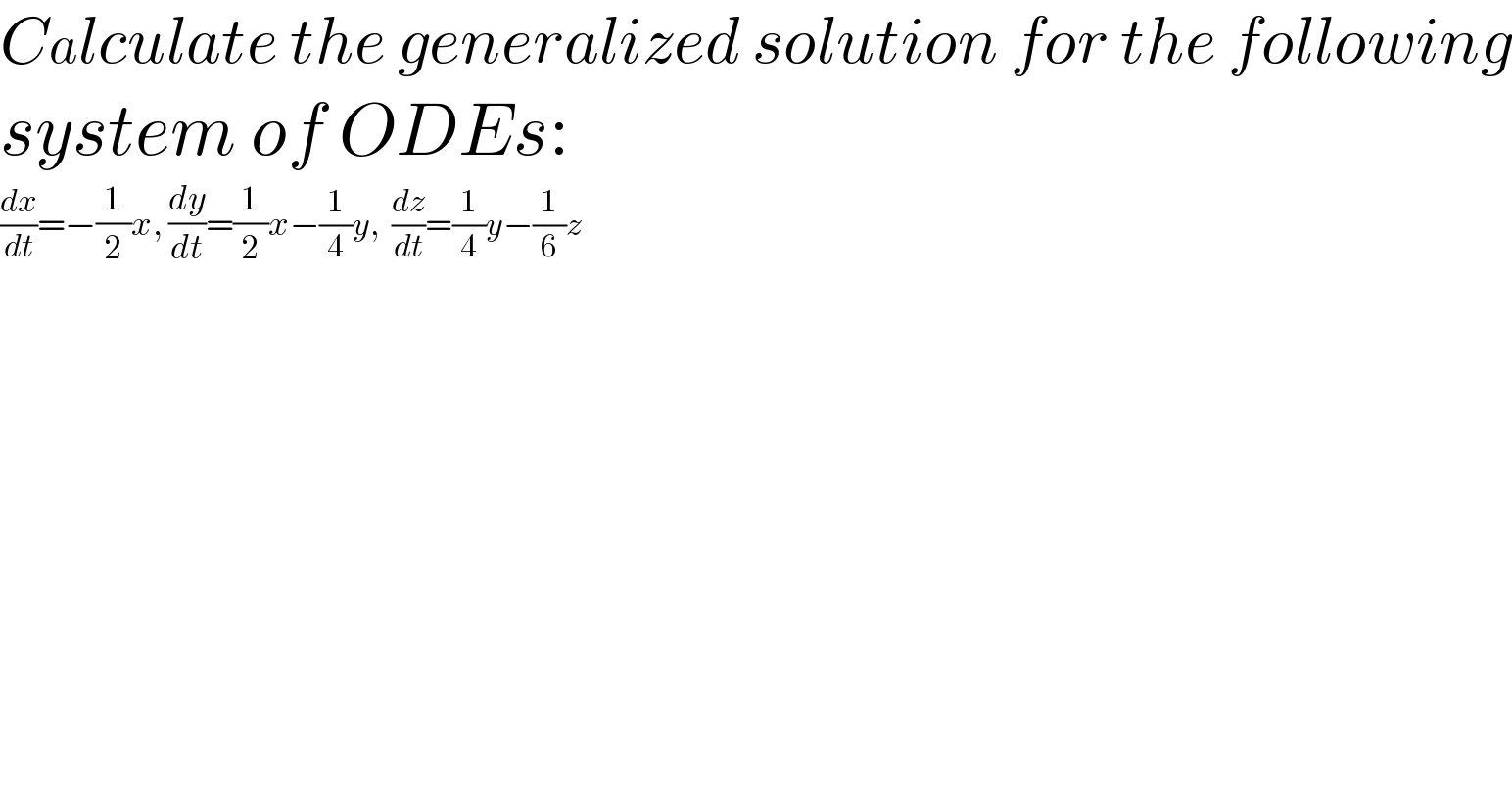
$${Calculate}\:{the}\:{generalized}\:{solution}\:{for}\:{the}\:{following} \\ $$$${system}\:{of}\:{ODEs}: \\ $$$$\frac{{dx}}{{dt}}=−\frac{\mathrm{1}}{\mathrm{2}}{x},\:\frac{{dy}}{{dt}}=\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{4}}{y},\:\:\frac{{dz}}{{dt}}=\frac{\mathrm{1}}{\mathrm{4}}{y}−\frac{\mathrm{1}}{\mathrm{6}}{z} \\ $$
Answered by mr W last updated on 07/May/24
![determinant (((−(1/2)−λ),0,0),((1/2),(−(1/4)−λ),0),(0,(1/4),(−(1/6)−λ)))=0 (−(1/2)−λ)(−(1/4)−λ)(−(1/6)−λ)=0 ⇒λ=−(1/2), −(1/4), −(1/6) V_1 = [((4/3)),((−(8/3))),(1) ] V_2 = [(0),((−(5/3))),(1) ] V_3 = [(0),(0),(1) ] [(x),(y),(z) ]=C_1 e^(−(t/2)) [((4/3)),((−(8/3))),(1) ]+C_2 e^(−(t/4)) [(0),((−(5/3))),(1) ]+C_3 e^(−(t/6)) [(0),(0),(1) ]](Q207124.png)
$$\begin{vmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}−\lambda}&{\mathrm{0}}&{\mathrm{0}}\\{\frac{\mathrm{1}}{\mathrm{2}}}&{−\frac{\mathrm{1}}{\mathrm{4}}−\lambda}&{\mathrm{0}}\\{\mathrm{0}}&{\frac{\mathrm{1}}{\mathrm{4}}}&{−\frac{\mathrm{1}}{\mathrm{6}}−\lambda}\end{vmatrix}=\mathrm{0} \\ $$$$\left(−\frac{\mathrm{1}}{\mathrm{2}}−\lambda\right)\left(−\frac{\mathrm{1}}{\mathrm{4}}−\lambda\right)\left(−\frac{\mathrm{1}}{\mathrm{6}}−\lambda\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda=−\frac{\mathrm{1}}{\mathrm{2}},\:−\frac{\mathrm{1}}{\mathrm{4}},\:−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${V}_{\mathrm{1}} =\begin{bmatrix}{\frac{\mathrm{4}}{\mathrm{3}}}\\{−\frac{\mathrm{8}}{\mathrm{3}}}\\{\mathrm{1}}\end{bmatrix} \\ $$$${V}_{\mathrm{2}} =\begin{bmatrix}{\mathrm{0}}\\{−\frac{\mathrm{5}}{\mathrm{3}}}\\{\mathrm{1}}\end{bmatrix} \\ $$$${V}_{\mathrm{3}} =\begin{bmatrix}{\mathrm{0}}\\{\mathrm{0}}\\{\mathrm{1}}\end{bmatrix} \\ $$$$\begin{bmatrix}{{x}}\\{{y}}\\{{z}}\end{bmatrix}={C}_{\mathrm{1}} {e}^{−\frac{{t}}{\mathrm{2}}} \begin{bmatrix}{\frac{\mathrm{4}}{\mathrm{3}}}\\{−\frac{\mathrm{8}}{\mathrm{3}}}\\{\mathrm{1}}\end{bmatrix}+{C}_{\mathrm{2}} {e}^{−\frac{{t}}{\mathrm{4}}} \begin{bmatrix}{\mathrm{0}}\\{−\frac{\mathrm{5}}{\mathrm{3}}}\\{\mathrm{1}}\end{bmatrix}+{C}_{\mathrm{3}} {e}^{−\frac{{t}}{\mathrm{6}}} \begin{bmatrix}{\mathrm{0}}\\{\mathrm{0}}\\{\mathrm{1}}\end{bmatrix} \\ $$
Commented by Wuji last updated on 07/May/24
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you},\:\mathrm{sir} \\ $$
