Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 76892 by john santu last updated on 31/Dec/19

Calculate ∫ ((√(9−x^2 ))/x^6 ) dx .

$$\mathcal{C}{alculate}\:\int\:\frac{\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }}{{x}^{\mathrm{6}} }\:{dx}\:. \\ $$

Answered by jagoll last updated on 31/Dec/19

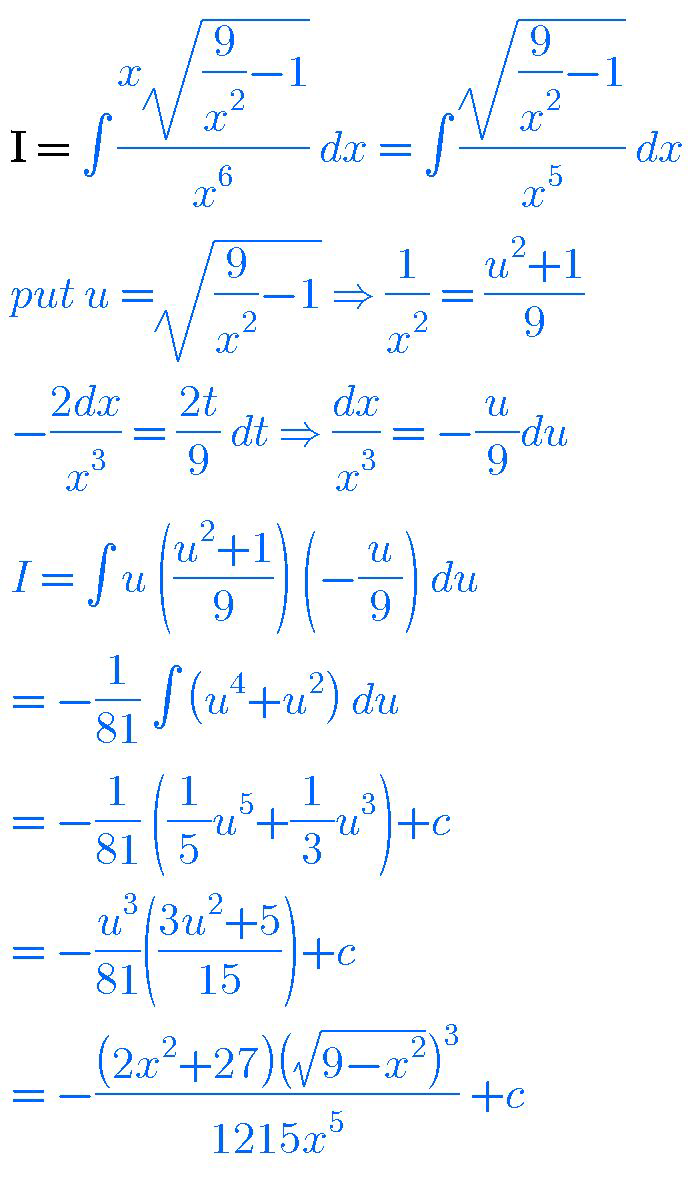
Answered by MJS last updated on 01/Jan/20

∫((√(9−x^2 ))/x^6 )dx= [t=(x/(√(9−x^2 ))) → dx=(((9−x^2 )^(3/2) )/9)dt] =(1/(81))∫(dt/t^4 )+(1/(81))∫(dt/t^6 )=−(1/(243t^3 ))−(1/(405t^5 ))= =−(((9−x^2 )^(3/2) )/(243x^3 ))−(((9−x^2 )^(5/2) )/(405x^5 ))=−(((2x^2 +27)(9−x^2 )^(3/2) )/(1215x^5 ))+C

$$\int\frac{\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }}{{x}^{\mathrm{6}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}}{\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }}\:\rightarrow\:{dx}=\frac{\left(\mathrm{9}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{9}}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{81}}\int\frac{{dt}}{{t}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{81}}\int\frac{{dt}}{{t}^{\mathrm{6}} }=−\frac{\mathrm{1}}{\mathrm{243}{t}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{405}{t}^{\mathrm{5}} }= \\ $$$$=−\frac{\left(\mathrm{9}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{243}{x}^{\mathrm{3}} }−\frac{\left(\mathrm{9}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{5}}{\mathrm{2}}} }{\mathrm{405}{x}^{\mathrm{5}} }=−\frac{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{27}\right)\left(\mathrm{9}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{1215}{x}^{\mathrm{5}} }+{C} \\ $$

Commented by jagoll last updated on 01/Jan/20

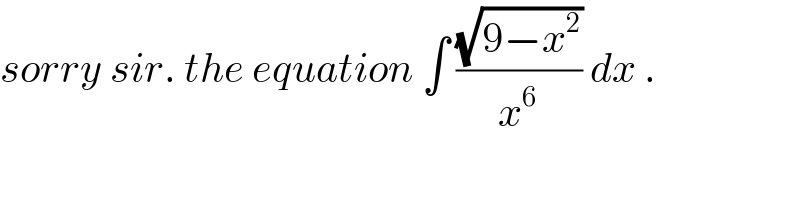
sorry sir. the equation ∫ ((√(9−x^2 ))/x^6 ) dx .

$${sorry}\:{sir}.\:{the}\:{equation}\:\int\:\frac{\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }}{{x}^{\mathrm{6}} }\:{dx}\:. \\ $$

Commented by MJS last updated on 01/Jan/20

thank you, it′s just a typo, I corrected it

$$\mathrm{thank}\:\mathrm{you},\:\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{a}\:\mathrm{typo},\:\mathrm{I}\:\mathrm{corrected}\:\mathrm{it} \\ $$

Commented by jagoll last updated on 01/Jan/20

thanks you sir

$${thanks}\:{you}\:{sir} \\ $$

Answered by petrochengula last updated on 03/Jan/20

let x=3sinθ⇒dx=3cosθdθ =∫((√(9−9sin^2 θ))/(3^6 sin^6 θ))3cosθdθ=(1/3^4 )∫((cos^2 θ)/(sin^6 θ))dθ =(1/(81))∫cot^2 θcosec^4 θdθ =(1/(81))∫cot^2 θ(1+cot^2 θ)cosec^2 θdθ let t=cotθ⇒−dt=cosec^2 θdθ =−(1/(81))∫t^2 (1+t^2 )dt =−(t^3 /(243))−(t^5 /(405))+c =−((cot^3 θ)/(243))−((cot^5 θ)/(405))+c =−(((cot(sin^(−1) ((x/3))))^3 )/(243))−(((cot(sin^(−1) ((x/3))))^5 )/(405))+c

$${let}\:{x}=\mathrm{3}{sin}\theta\Rightarrow{dx}=\mathrm{3}{cos}\theta{d}\theta \\ $$$$=\int\frac{\sqrt{\mathrm{9}−\mathrm{9}{sin}^{\mathrm{2}} \theta}}{\mathrm{3}^{\mathrm{6}} {sin}^{\mathrm{6}} \theta}\mathrm{3}{cos}\theta{d}\theta=\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{4}} }\int\frac{{cos}^{\mathrm{2}} \theta}{{sin}^{\mathrm{6}} \theta}{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{81}}\int{cot}^{\mathrm{2}} \theta{cosec}^{\mathrm{4}} \theta{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{81}}\int{cot}^{\mathrm{2}} \theta\left(\mathrm{1}+{cot}^{\mathrm{2}} \theta\right){cosec}^{\mathrm{2}} \theta{d}\theta \\ $$$${let}\:{t}={cot}\theta\Rightarrow−{dt}={cosec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=−\frac{\mathrm{1}}{\mathrm{81}}\int{t}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt} \\ $$$$=−\frac{{t}^{\mathrm{3}} }{\mathrm{243}}−\frac{{t}^{\mathrm{5}} }{\mathrm{405}}+{c} \\ $$$$=−\frac{{cot}^{\mathrm{3}} \theta}{\mathrm{243}}−\frac{{cot}^{\mathrm{5}} \theta}{\mathrm{405}}+{c} \\ $$$$=−\frac{\left({cot}\left({sin}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{3}}\right)\right)\right)^{\mathrm{3}} }{\mathrm{243}}−\frac{\left({cot}\left({sin}^{−\mathrm{1}} \left(\frac{{x}}{\mathrm{3}}\right)\right)\right)^{\mathrm{5}} }{\mathrm{405}}+{c} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com