Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 132124 by Chhing last updated on 11/Feb/21

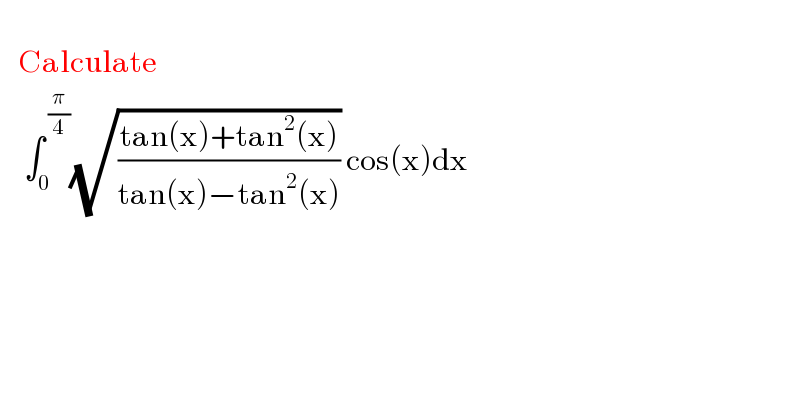
Calculate ∫_0 ^( (π/4)) (√((tan(x)+tan^2 (x))/(tan(x)−tan^2 (x)))) cos(x)dx

$$ \\ $$$$\:\:\:\mathrm{Calculate} \\ $$$$\:\:\:\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \sqrt{\frac{\mathrm{tan}\left(\mathrm{x}\right)+\mathrm{tan}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{tan}\left(\mathrm{x}\right)−\mathrm{tan}^{\mathrm{2}} \left(\mathrm{x}\right)}}\:\mathrm{cos}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\:\: \\ $$

Commented by liberty last updated on 11/Feb/21

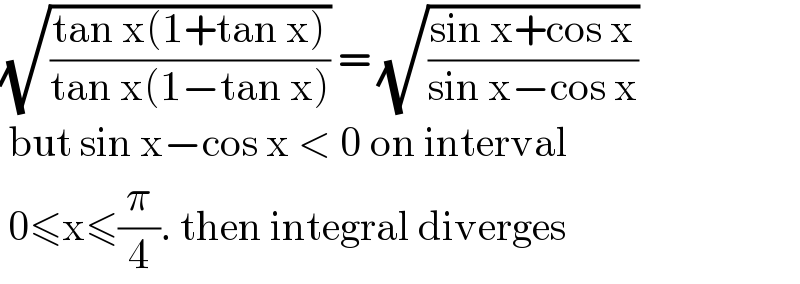
(√((tan x(1+tan x))/(tan x(1−tan x)))) = (√((sin x+cos x)/(sin x−cos x))) but sin x−cos x < 0 on interval 0≤x≤(π/4). then integral diverges

$$\sqrt{\frac{\mathrm{tan}\:\mathrm{x}\left(\mathrm{1}+\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{tan}\:\mathrm{x}\left(\mathrm{1}−\mathrm{tan}\:\mathrm{x}\right)}}\:=\:\sqrt{\frac{\mathrm{sin}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}}} \\ $$$$\:\mathrm{but}\:\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\:<\:\mathrm{0}\:\mathrm{on}\:\mathrm{interval} \\ $$$$\:\mathrm{0}\leqslant\mathrm{x}\leqslant\frac{\pi}{\mathrm{4}}.\:\mathrm{then}\:\mathrm{integral}\:\mathrm{diverges} \\ $$

Commented by prakash jain last updated on 11/Feb/21

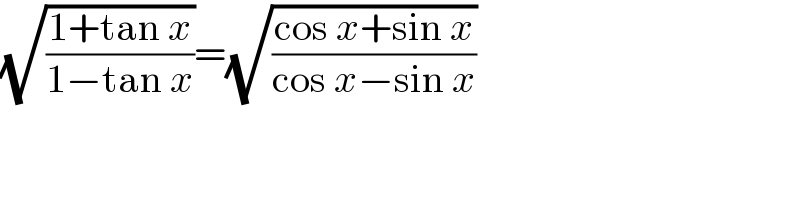
(√((1+tan x)/(1−tan x)))=(√((cos x+sin x)/(cos x−sin x)))

$$\sqrt{\frac{\mathrm{1}+\mathrm{tan}\:{x}}{\mathrm{1}−\mathrm{tan}\:{x}}}=\sqrt{\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}} \\ $$

Answered by Ar Brandon last updated on 11/Feb/21

I=∫_0 ^(π/4) (√((tanx+tan^2 x)/(tanx−tan^2 x)))∙cosxdx =∫_0 ^(π/4) (√((cosx+sinx)/(cosx−sinx)))∙cosxdx=∫_0 ^(π/4) ((cosx+sinx)/( (√(cos2x))))∙cosxdx =(1/2)∫_0 ^(π/4) ((1+cos2x)/( (√(cos2x))))dx+(1/2)∫_0 ^(π/4) ((sin2x)/( (√(cos2x))))dx u^2 =cos2x , 2udu=−2(√(1−u^4 )) =(1/4)∫_0 ^1 ((1+u)/( (√u)))∙(du/( (√(1−u^2 ))))−[((√(cos2x))/2)]_0 ^(π/4) =(1/4)∫_0 ^1 ((1+u)/( (√(u−u^3 ))))du+(1/2)

$$\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\frac{\mathrm{tanx}+\mathrm{tan}^{\mathrm{2}} \mathrm{x}}{\mathrm{tanx}−\mathrm{tan}^{\mathrm{2}} \mathrm{x}}}\centerdot\mathrm{cosxdx} \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\frac{\mathrm{cosx}+\mathrm{sinx}}{\mathrm{cosx}−\mathrm{sinx}}}\centerdot\mathrm{cosxdx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{cosx}+\mathrm{sinx}}{\:\sqrt{\mathrm{cos2x}}}\centerdot\mathrm{cosxdx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}+\mathrm{cos2x}}{\:\sqrt{\mathrm{cos2x}}}\mathrm{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{sin2x}}{\:\sqrt{\mathrm{cos2x}}}\mathrm{dx} \\ $$$$\mathrm{u}^{\mathrm{2}} =\mathrm{cos2x}\:,\:\mathrm{2udu}=−\mathrm{2}\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{4}} } \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+\mathrm{u}}{\:\sqrt{\mathrm{u}}}\centerdot\frac{\mathrm{du}}{\:\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}−\left[\frac{\sqrt{\mathrm{cos2x}}}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} =\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+\mathrm{u}}{\:\sqrt{\mathrm{u}−\mathrm{u}^{\mathrm{3}} }}\mathrm{du}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by Dwaipayan Shikari last updated on 17/Feb/21

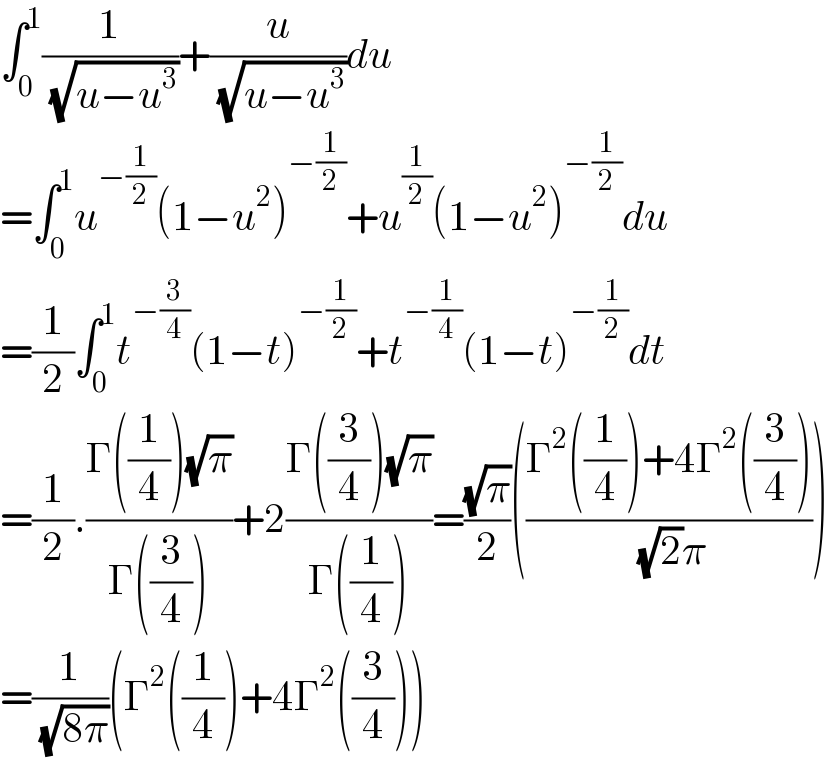
∫_0 ^1 (1/( (√(u−u^3 ))))+(u/( (√(u−u^3 ))))du =∫_0 ^1 u^(−(1/2)) (1−u^2 )^(−(1/2)) +u^(1/2) (1−u^2 )^(−(1/2)) du =(1/2)∫_0 ^1 t^(−(3/4)) (1−t)^(−(1/2)) +t^(−(1/4)) (1−t)^(−(1/2)) dt =(1/2).((Γ((1/4))(√π))/(Γ((3/4))))+2((Γ((3/4))(√π))/(Γ((1/4))))=((√π)/2)(((Γ^2 ((1/4))+4Γ^2 ((3/4)))/( (√2)π))) =(1/( (√(8π))))(Γ^2 ((1/4))+4Γ^2 ((3/4)))

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{{u}−{u}^{\mathrm{3}} }}+\frac{{u}}{\:\sqrt{{u}−{u}^{\mathrm{3}} }}{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} +{u}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} +{t}^{−\frac{\mathrm{1}}{\mathrm{4}}} \left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\sqrt{\pi}}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}+\mathrm{2}\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\sqrt{\pi}}{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}=\frac{\sqrt{\pi}}{\mathrm{2}}\left(\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{4}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\:\sqrt{\mathrm{2}}\pi}\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{8}\pi}}\left(\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{4}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com