Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 201257 by BaliramKumar last updated on 02/Dec/23

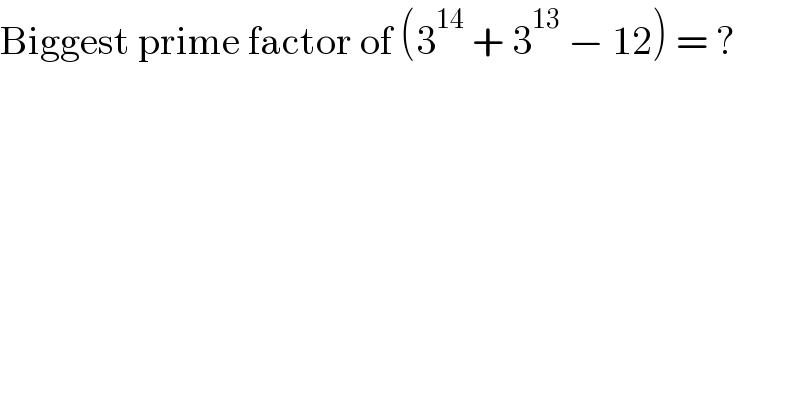
Biggest prime factor of (3^(14) + 3^(13) − 12) = ?

$$\mathrm{Biggest}\:\mathrm{prime}\:\mathrm{factor}\:\mathrm{of}\:\left(\mathrm{3}^{\mathrm{14}} \:+\:\mathrm{3}^{\mathrm{13}} \:−\:\mathrm{12}\right)\:=\:? \\ $$

Answered by Rasheed.Sindhi last updated on 02/Dec/23

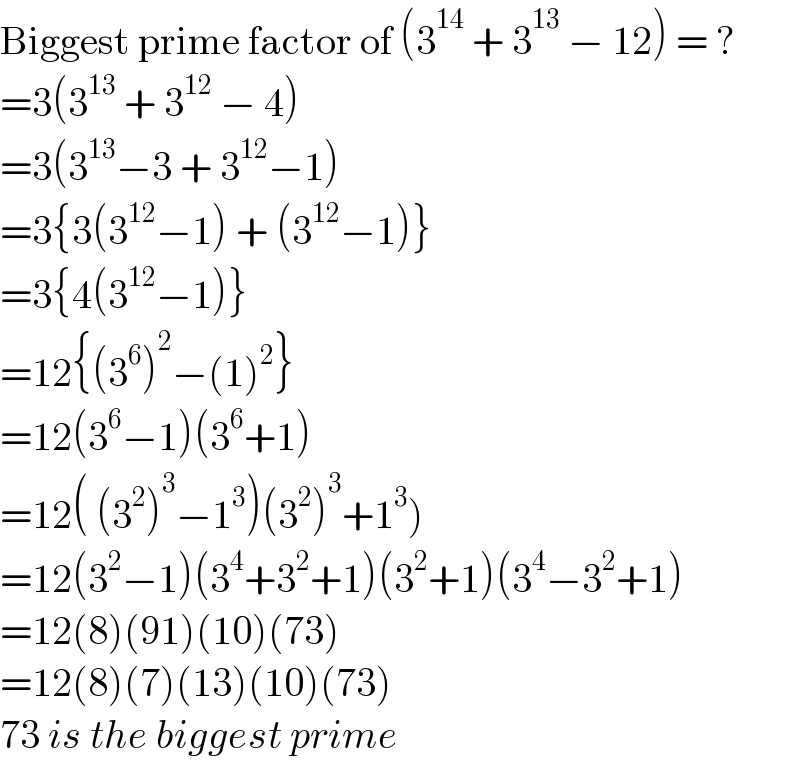
Biggest prime factor of (3^(14) + 3^(13) − 12) = ? =3(3^(13) + 3^(12) − 4) =3(3^(13) −3 + 3^(12) −1) =3{3(3^(12) −1) + (3^(12) −1)} =3{4(3^(12) −1)} =12{(3^6 )^2 −(1)^2 } =12(3^6 −1)(3^6 +1) =12( (3^2 )^3 −1^3 )(3^2 )^3 +1^3 ) =12(3^2 −1)(3^4 +3^2 +1)(3^2 +1)(3^4 −3^2 +1) =12(8)(91)(10)(73) =12(8)(7)(13)(10)(73) 73 is the biggest prime

$$\mathrm{Biggest}\:\mathrm{prime}\:\mathrm{factor}\:\mathrm{of}\:\left(\mathrm{3}^{\mathrm{14}} \:+\:\mathrm{3}^{\mathrm{13}} \:−\:\mathrm{12}\right)\:=\:? \\ $$$$=\mathrm{3}\left(\mathrm{3}^{\mathrm{13}} \:+\:\mathrm{3}^{\mathrm{12}} \:−\:\mathrm{4}\right) \\ $$$$=\mathrm{3}\left(\mathrm{3}^{\mathrm{13}} −\mathrm{3}\:+\:\mathrm{3}^{\mathrm{12}} −\mathrm{1}\right) \\ $$$$=\mathrm{3}\left\{\mathrm{3}\left(\mathrm{3}^{\mathrm{12}} −\mathrm{1}\right)\:+\:\left(\mathrm{3}^{\mathrm{12}} −\mathrm{1}\right)\right\} \\ $$$$=\mathrm{3}\left\{\mathrm{4}\left(\mathrm{3}^{\mathrm{12}} −\mathrm{1}\right)\right\} \\ $$$$=\mathrm{12}\left\{\left(\mathrm{3}^{\mathrm{6}} \right)^{\mathrm{2}} −\left(\mathrm{1}\right)^{\mathrm{2}} \right\} \\ $$$$=\mathrm{12}\left(\mathrm{3}^{\mathrm{6}} −\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{6}} +\mathrm{1}\right) \\ $$$$\left.=\mathrm{12}\left(\:\left(\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{1}^{\mathrm{3}} \right)\left(\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{3}} +\mathrm{1}^{\mathrm{3}} \right) \\ $$$$=\mathrm{12}\left(\mathrm{3}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{4}} +\mathrm{3}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{4}} −\mathrm{3}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$=\mathrm{12}\left(\mathrm{8}\right)\left(\mathrm{91}\right)\left(\mathrm{10}\right)\left(\mathrm{73}\right) \\ $$$$=\mathrm{12}\left(\mathrm{8}\right)\left(\mathrm{7}\right)\left(\mathrm{13}\right)\left(\mathrm{10}\right)\left(\mathrm{73}\right) \\ $$$$\mathrm{73}\:{is}\:{the}\:{biggest}\:{prime} \\ $$

Commented by BaliramKumar last updated on 02/Dec/23

Nice solution thanks

$$\mathrm{Nice}\:\mathrm{solution} \\ $$$$\mathrm{thanks} \\ $$

Answered by Rasheed.Sindhi last updated on 02/Dec/23

Another Way 3^(14) + 3^(13) − 12) =3^(13) (3+1)−12 =4(3^(13) −3) =4.3(3^(12) −1) =12(3^6 −1)(3^6 +1) =12{(3^2 )^3 −1^3 }{(3^2 )^3 +1^3 } =12(3^2 −1)(3^4 +3^2 +1)(3^2 +1)(3^4 −3^2 +1) =12.8.91.10.73 =12.8.7.13.10.73⇒73 is the biggest prime

$$\mathbb{A}\mathrm{nother}\:\mathbb{W}\mathrm{ay} \\ $$$$\left.\mathrm{3}^{\mathrm{14}} \:+\:\mathrm{3}^{\mathrm{13}} \:−\:\mathrm{12}\right)\: \\ $$$$=\mathrm{3}^{\mathrm{13}} \left(\mathrm{3}+\mathrm{1}\right)−\mathrm{12} \\ $$$$=\mathrm{4}\left(\mathrm{3}^{\mathrm{13}} −\mathrm{3}\right) \\ $$$$=\mathrm{4}.\mathrm{3}\left(\mathrm{3}^{\mathrm{12}} −\mathrm{1}\right) \\ $$$$=\mathrm{12}\left(\mathrm{3}^{\mathrm{6}} −\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{6}} +\mathrm{1}\right) \\ $$$$=\mathrm{12}\left\{\left(\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{3}} −\mathrm{1}^{\mathrm{3}} \right\}\left\{\left(\mathrm{3}^{\mathrm{2}} \right)^{\mathrm{3}} +\mathrm{1}^{\mathrm{3}} \right\} \\ $$$$=\mathrm{12}\left(\mathrm{3}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{4}} +\mathrm{3}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{4}} −\mathrm{3}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$=\mathrm{12}.\mathrm{8}.\mathrm{91}.\mathrm{10}.\mathrm{73} \\ $$$$=\mathrm{12}.\mathrm{8}.\mathrm{7}.\mathrm{13}.\mathrm{10}.\mathrm{73}\Rightarrow\mathrm{73}\:{is}\:{the}\:{biggest}\:{prime} \\ $$

Commented by Rasheed.Sindhi last updated on 03/Dec/23

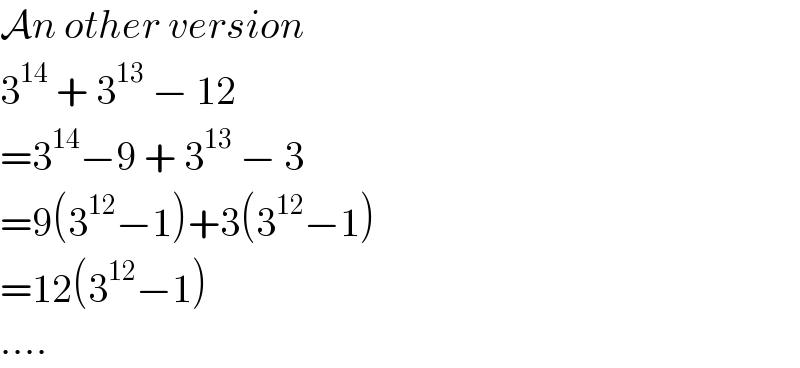
An other version 3^(14) + 3^(13) − 12 =3^(14) −9 + 3^(13) − 3 =9(3^(12) −1)+3(3^(12) −1) =12(3^(12) −1) ....

$$\mathcal{A}{n}\:{other}\:{version} \\ $$$$\mathrm{3}^{\mathrm{14}} \:+\:\mathrm{3}^{\mathrm{13}} \:−\:\mathrm{12} \\ $$$$=\mathrm{3}^{\mathrm{14}} −\mathrm{9}\:+\:\mathrm{3}^{\mathrm{13}} \:−\:\mathrm{3} \\ $$$$=\mathrm{9}\left(\mathrm{3}^{\mathrm{12}} −\mathrm{1}\right)+\mathrm{3}\left(\mathrm{3}^{\mathrm{12}} −\mathrm{1}\right) \\ $$$$=\mathrm{12}\left(\mathrm{3}^{\mathrm{12}} −\mathrm{1}\right) \\ $$$$.... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com