
Question Number 107484 by bemath last updated on 11/Aug/20
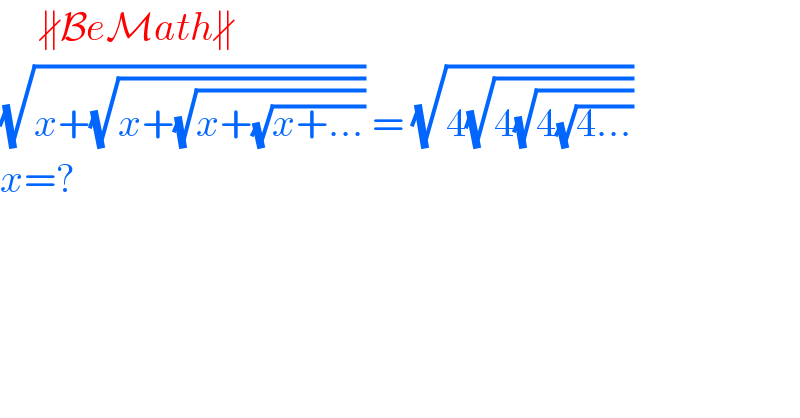
$$\:\:\:\:\:\nparallel\mathcal{B}{e}\mathcal{M}{ath}\nparallel \\ $$$$\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}}}\:=\:\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}...}}}} \\ $$$${x}=?\: \\ $$
Answered by john santu last updated on 11/Aug/20
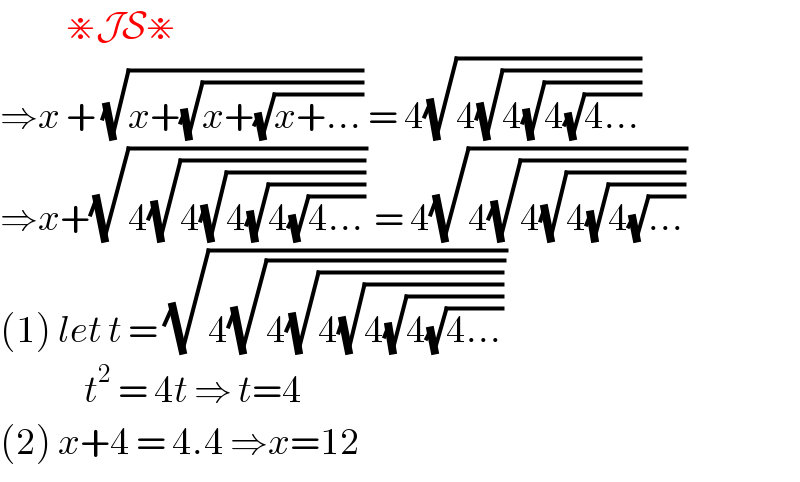
$$\:\:\:\:\:\:\:\:\:\:\:\divideontimes\mathcal{JS}\divideontimes \\ $$$$\Rightarrow{x}\:+\:\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+...}}}\:=\:\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}...}}}} \\ $$$$\Rightarrow{x}+\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}...}}}}}\:=\:\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{...}}}}} \\ $$$$\left(\mathrm{1}\right)\:{let}\:{t}\:=\:\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}...}}}}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{t}^{\mathrm{2}} \:=\:\mathrm{4}{t}\:\Rightarrow\:{t}=\mathrm{4}\: \\ $$$$\left(\mathrm{2}\right)\:{x}+\mathrm{4}\:=\:\mathrm{4}.\mathrm{4}\:\Rightarrow{x}=\mathrm{12}\: \\ $$
Answered by Dwaipayan Shikari last updated on 11/Aug/20

$$\sqrt{{x}+\sqrt{{x}+\sqrt{{x}+\sqrt{{x}....\:}}}}\:\:={p} \\ $$$${x}+{p}={p}^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} −{p}−{x}=\mathrm{0} \\ $$$${p}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{x}}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}\sqrt{\mathrm{4}}}}}}}={a} \\ $$$$\mathrm{4}{a}={a}^{\mathrm{2}} \\ $$$${a}=\mathrm{4} \\ $$$$\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4}{x}}\:=\mathrm{8} \\ $$$$\mathrm{1}+\mathrm{4}{x}=\mathrm{49} \\ $$$${x}=\mathrm{12} \\ $$
