Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 107945 by bemath last updated on 13/Aug/20

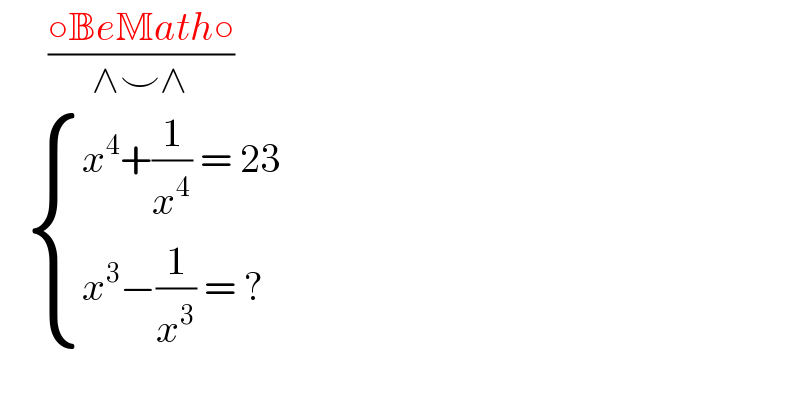
((○BeMath○)/(∧⌣∧)) { ((x^4 +(1/x^4 ) = 23)),((x^3 −(1/x^3 ) = ?)) :}

$$\:\:\:\:\:\:\frac{\circ\mathbb{B}{e}\mathbb{M}{ath}\circ}{\wedge\smile\wedge} \\ $$$$\:\:\:\begin{cases}{{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:=\:\mathrm{23}}\\{{x}^{\mathrm{3}} −\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:=\:?}\end{cases} \\ $$

Answered by $@y@m last updated on 13/Aug/20

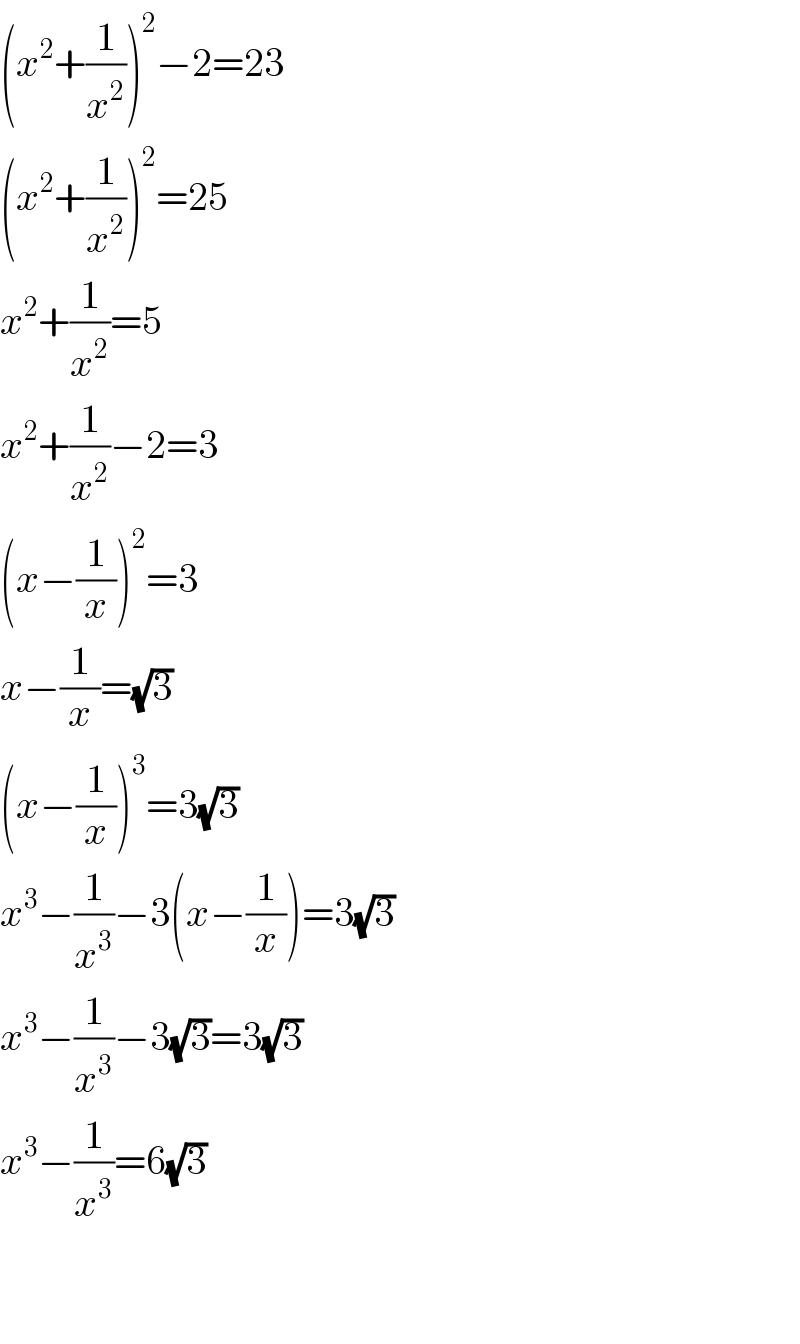
(x^2 +(1/x^2 ))^2 −2=23 (x^2 +(1/x^2 ))^2 =25 x^2 +(1/x^2 )=5 x^2 +(1/x^2 )−2=3 (x−(1/x))^2 =3 x−(1/x)=(√3) (x−(1/x))^3 =3(√3) x^3 −(1/x^3 )−3(x−(1/x))=3(√3) x^3 −(1/x^3 )−3(√3)=3(√3) x^3 −(1/x^3 )=6(√3)

$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{23} \\ $$$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{25} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{5} \\ $$$${x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{2}=\mathrm{3} \\ $$$$\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\mathrm{3} \\ $$$${x}−\frac{\mathrm{1}}{{x}}=\sqrt{\mathrm{3}} \\ $$$$\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} =\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{1}}{{x}^{\mathrm{3}} }−\mathrm{3}\left({x}−\frac{\mathrm{1}}{{x}}\right)=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{1}}{{x}^{\mathrm{3}} }−\mathrm{3}\sqrt{\mathrm{3}}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\mathrm{6}\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 13/Aug/20

Nice!

$$\:\:\mathrm{Nic}{e}! \\ $$

Commented by Her_Majesty last updated on 13/Aug/20

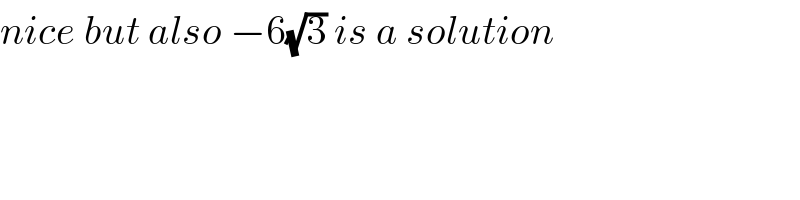
nice but also −6(√3) is a solution

$${nice}\:{but}\:{also}\:−\mathrm{6}\sqrt{\mathrm{3}}\:{is}\:{a}\:{solution} \\ $$

Commented by bemath last updated on 13/Aug/20

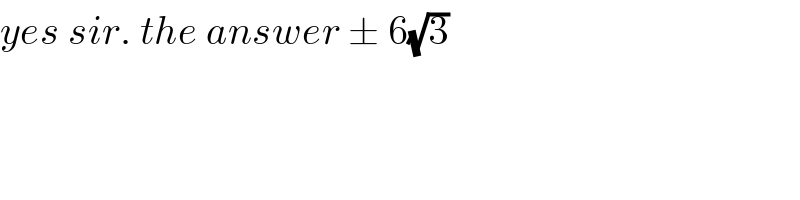
yes sir. the answer ± 6(√3)

$${yes}\:{sir}.\:{the}\:{answer}\:\pm\:\mathrm{6}\sqrt{\mathrm{3}} \\ $$

Answered by 1549442205PVT last updated on 13/Aug/20

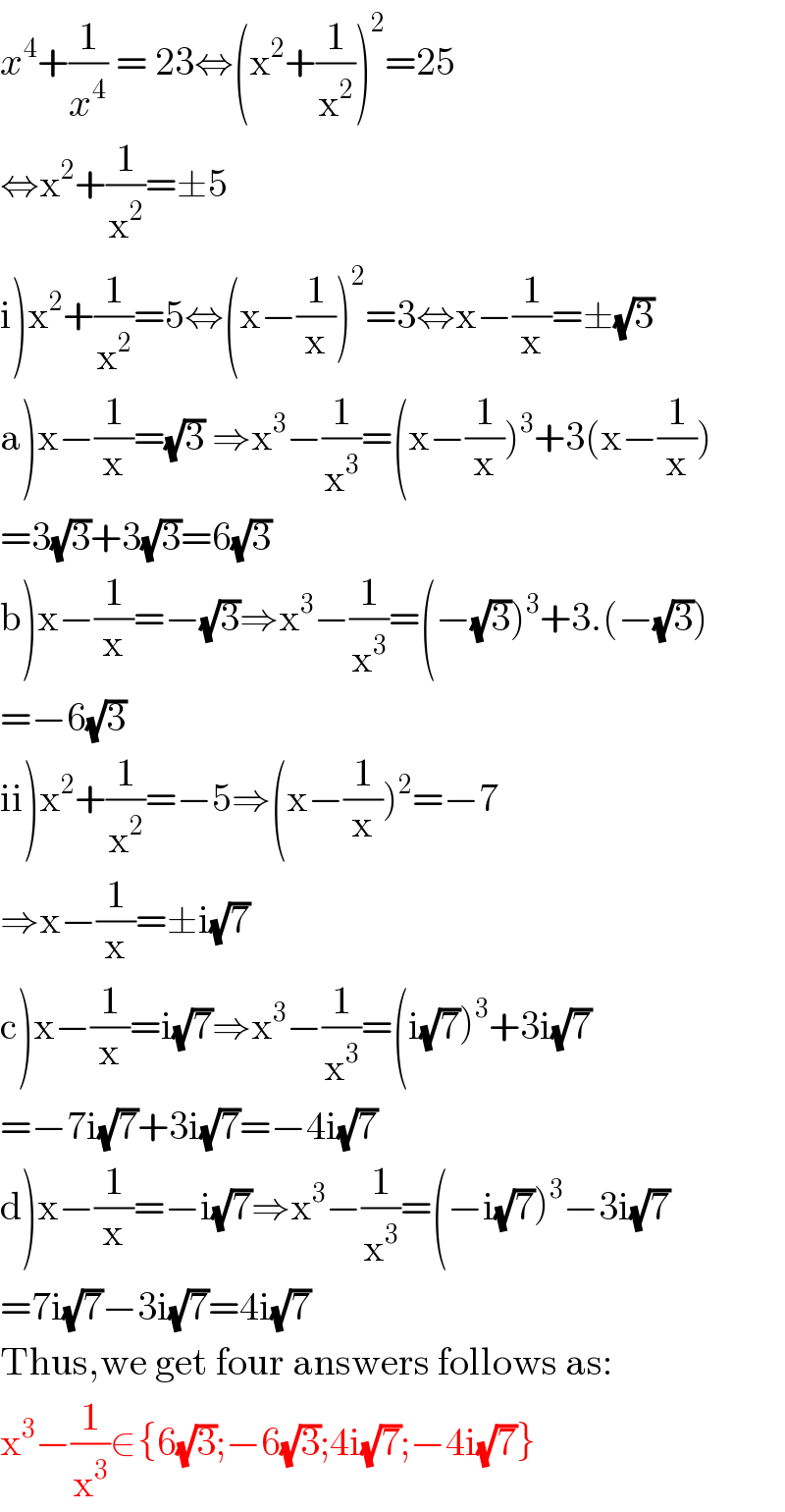
x^4 +(1/x^4 ) = 23⇔(x^2 +(1/x^2 ))^2 =25 ⇔x^2 +(1/x^2 )=±5 i)x^2 +(1/x^2 )=5⇔(x−(1/x))^2 =3⇔x−(1/x)=±(√3) a)x−(1/x)=(√3) ⇒x^3 −(1/x^3 )=(x−(1/x))^3 +3(x−(1/x)) =3(√3)+3(√3)=6(√3) b)x−(1/x)=−(√3)⇒x^3 −(1/x^3 )=(−(√3))^3 +3.(−(√3)) =−6(√3) ii)x^2 +(1/x^2 )=−5⇒(x−(1/x))^2 =−7 ⇒x−(1/x)=±i(√7) c)x−(1/x)=i(√7)⇒x^3 −(1/x^3 )=(i(√7))^3 +3i(√7) =−7i(√7)+3i(√7)=−4i(√7) d)x−(1/x)=−i(√7)⇒x^3 −(1/x^3 )=(−i(√7))^3 −3i(√7) =7i(√7)−3i(√7)=4i(√7) Thus,we get four answers follows as: x^3 −(1/x^3 )∈{6(√3);−6(√3);4i(√7);−4i(√7)}

$${x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:=\:\mathrm{23}\Leftrightarrow\left(\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{25} \\ $$$$\Leftrightarrow\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\pm\mathrm{5} \\ $$$$\left.\mathrm{i}\right)\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{5}\Leftrightarrow\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} =\mathrm{3}\Leftrightarrow\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\pm\sqrt{\mathrm{3}} \\ $$$$\left.\mathrm{a}\right)\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\sqrt{\mathrm{3}}\:\Rightarrow\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }=\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{3}} +\mathrm{3}\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$=\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{3}\sqrt{\mathrm{3}}=\mathrm{6}\sqrt{\mathrm{3}} \\ $$$$\left.\mathrm{b}\right)\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=−\sqrt{\mathrm{3}}\Rightarrow\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }=\left(−\sqrt{\mathrm{3}}\right)^{\mathrm{3}} +\mathrm{3}.\left(−\sqrt{\mathrm{3}}\right) \\ $$$$=−\mathrm{6}\sqrt{\mathrm{3}} \\ $$$$\left.\mathrm{ii}\right)\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=−\mathrm{5}\Rightarrow\left(\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}\right)^{\mathrm{2}} =−\mathrm{7} \\ $$$$\Rightarrow\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\pm\mathrm{i}\sqrt{\mathrm{7}} \\ $$$$\left.\mathrm{c}\right)\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=\mathrm{i}\sqrt{\mathrm{7}}\Rightarrow\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }=\left(\mathrm{i}\sqrt{\mathrm{7}}\right)^{\mathrm{3}} +\mathrm{3i}\sqrt{\mathrm{7}} \\ $$$$=−\mathrm{7i}\sqrt{\mathrm{7}}+\mathrm{3i}\sqrt{\mathrm{7}}=−\mathrm{4i}\sqrt{\mathrm{7}} \\ $$$$\left.\mathrm{d}\right)\mathrm{x}−\frac{\mathrm{1}}{\mathrm{x}}=−\mathrm{i}\sqrt{\mathrm{7}}\Rightarrow\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }=\left(−\mathrm{i}\sqrt{\mathrm{7}}\right)^{\mathrm{3}} −\mathrm{3i}\sqrt{\mathrm{7}} \\ $$$$=\mathrm{7i}\sqrt{\mathrm{7}}−\mathrm{3i}\sqrt{\mathrm{7}}=\mathrm{4i}\sqrt{\mathrm{7}} \\ $$$$\mathrm{Thus},\mathrm{we}\:\mathrm{get}\:\mathrm{four}\:\mathrm{answers}\:\mathrm{follows}\:\mathrm{as}: \\ $$$$\mathrm{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\in\left\{\mathrm{6}\sqrt{\mathrm{3}};−\mathrm{6}\sqrt{\mathrm{3}};\mathrm{4i}\sqrt{\mathrm{7}};−\mathrm{4i}\sqrt{\mathrm{7}}\right\} \\ $$

Answered by Rasheed.Sindhi last updated on 13/Aug/20

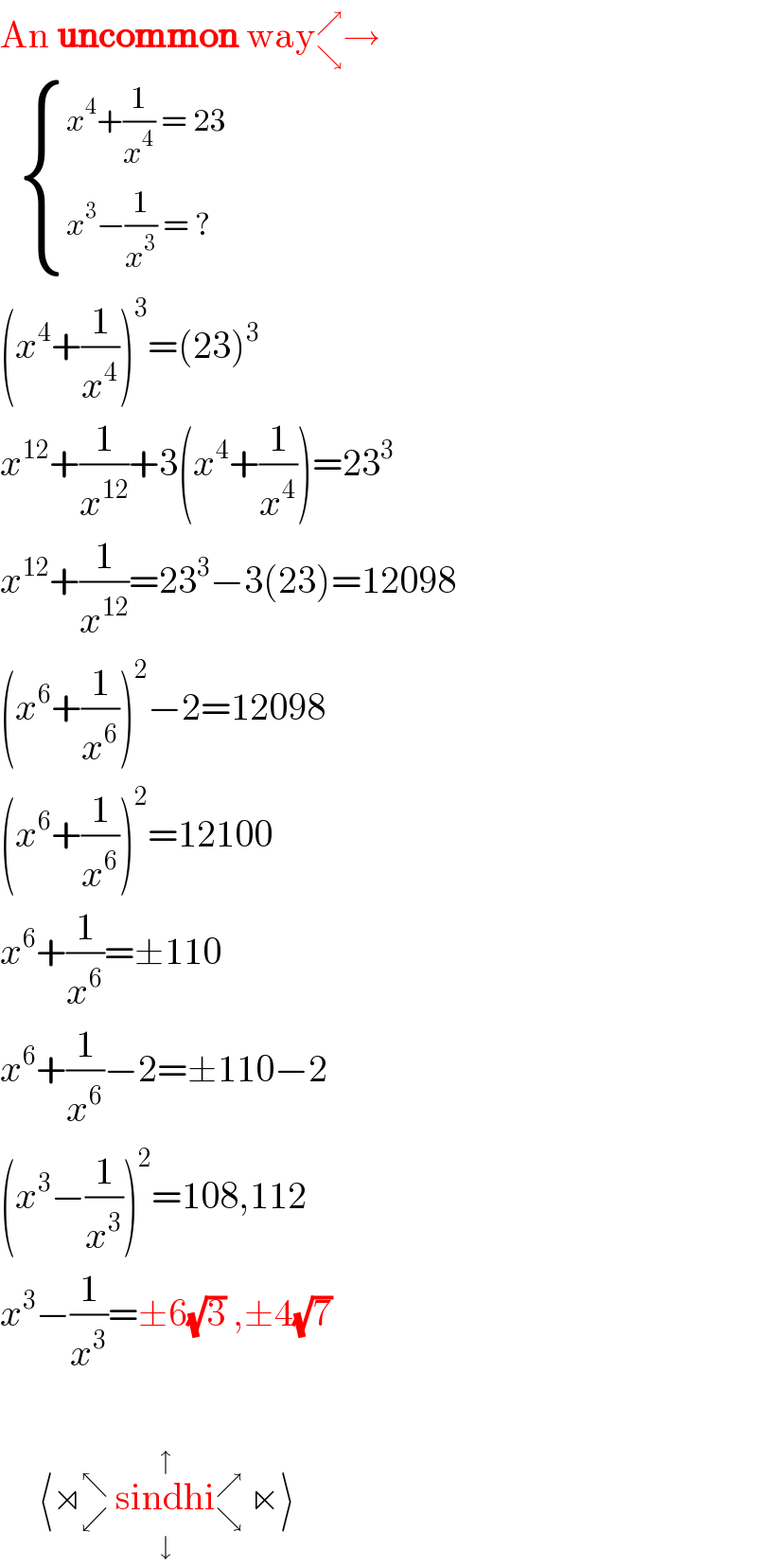
An uncommon way_↘ ^↗ → { ((x^4 +(1/x^4 ) = 23)),((x^3 −(1/x^3 ) = ?)) :} (x^4 +(1/x^4 ))^3 =(23)^3 x^(12) +(1/x^(12) )+3(x^4 +(1/x^4 ))=23^3 x^(12) +(1/x^(12) )=23^3 −3(23)=12098 (x^6 +(1/x^6 ))^2 −2=12098 (x^6 +(1/x^6 ))^2 =12100 x^6 +(1/x^6 )=±110 x^6 +(1/x^6 )−2=±110−2 (x^3 −(1/x^3 ))^2 =108,112 x^3 −(1/x^3 )=±6(√3) ,±4(√7) ⟨⋊_↙ ^↖ sindhi_↘ ^↗ ⋉⟩_(↓) ^(↑) _ ^

$$\mathrm{An}\:\boldsymbol{\mathrm{uncommon}}\:\mathrm{way}_{\searrow} ^{\nearrow} \rightarrow \\ $$$$\:\:\:\begin{cases}{{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:=\:\mathrm{23}}\\{{x}^{\mathrm{3}} −\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\:=\:?}\end{cases} \\ $$$$\left({x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)^{\mathrm{3}} =\left(\mathrm{23}\right)^{\mathrm{3}} \\ $$$${x}^{\mathrm{12}} +\frac{\mathrm{1}}{{x}^{\mathrm{12}} }+\mathrm{3}\left({x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)=\mathrm{23}^{\mathrm{3}} \\ $$$${x}^{\mathrm{12}} +\frac{\mathrm{1}}{{x}^{\mathrm{12}} }=\mathrm{23}^{\mathrm{3}} −\mathrm{3}\left(\mathrm{23}\right)=\mathrm{12098} \\ $$$$\left({x}^{\mathrm{6}} +\frac{\mathrm{1}}{{x}^{\mathrm{6}} }\right)^{\mathrm{2}} −\mathrm{2}=\mathrm{12098} \\ $$$$\left({x}^{\mathrm{6}} +\frac{\mathrm{1}}{{x}^{\mathrm{6}} }\right)^{\mathrm{2}} =\mathrm{12100} \\ $$$${x}^{\mathrm{6}} +\frac{\mathrm{1}}{{x}^{\mathrm{6}} }=\pm\mathrm{110} \\ $$$${x}^{\mathrm{6}} +\frac{\mathrm{1}}{{x}^{\mathrm{6}} }−\mathrm{2}=\pm\mathrm{110}−\mathrm{2} \\ $$$$\left({x}^{\mathrm{3}} −\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)^{\mathrm{2}} =\mathrm{108},\mathrm{112} \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{1}}{{x}^{\mathrm{3}} }=\pm\mathrm{6}\sqrt{\mathrm{3}}\:,\pm\mathrm{4}\sqrt{\mathrm{7}}\: \\ $$$$ \\ $$$$\:\:\:\:\:\underset{\downarrow} {\overset{\uparrow} {\langle\rtimes_{\swarrow} ^{\nwarrow} \:\mathrm{sindhi}_{\searrow} ^{\nearrow} \:\ltimes\rangle}}\:\:_{\:} ^{\:} \:\: \\ $$

Commented by bemath last updated on 13/Aug/20

cooll

$${cooll} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com