
Question Number 107690 by bemath last updated on 12/Aug/20

$$\:\:\:\:\:\:\:\:``\mathcal{B}{e}\mathcal{M}{ath}`` \\ $$$${Let}\:{the}\:{complex}\:{number}\:{z}\:{satisfies}\:{the} \\ $$$${equation}\:\mathrm{3}\left({z}−\mathrm{1}\right)=\:{i}\left({z}+\mathrm{1}\right)\: \\ $$$$\left(\mathrm{1}\right)\:{find}\:{z}\:{in}\:{the}\:{form}\:{a}+{bi}\:{where}\:{a},{b}\:\in\mathbb{R}\: \\ $$$$\left(\mathrm{2}\right)\:{find}\:{the}\:{value}\:{of}\:\mid{z}\mid\:{and}\:\mid{z}−{z}^{\ast} \mid\: \\ $$$$ \\ $$
Answered by mr W last updated on 12/Aug/20
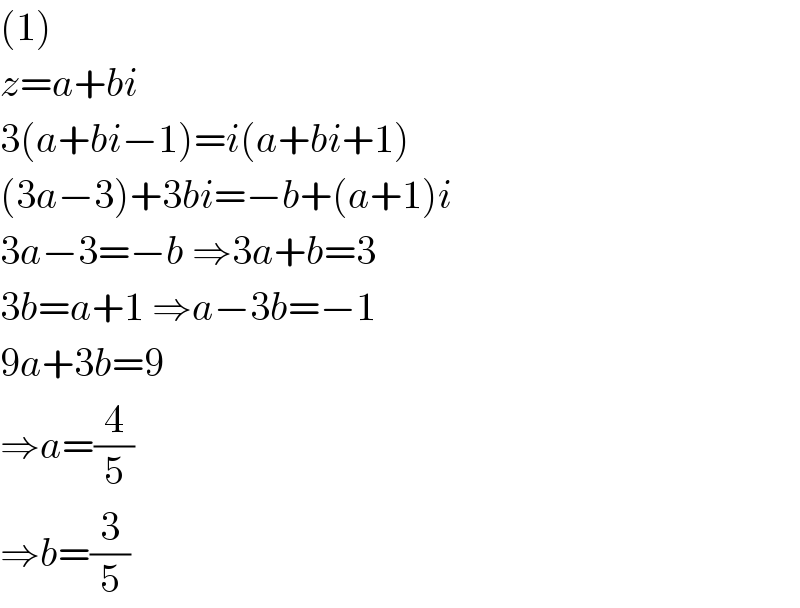
$$\left(\mathrm{1}\right) \\ $$$${z}={a}+{bi} \\ $$$$\mathrm{3}\left({a}+{bi}−\mathrm{1}\right)={i}\left({a}+{bi}+\mathrm{1}\right) \\ $$$$\left(\mathrm{3}{a}−\mathrm{3}\right)+\mathrm{3}{bi}=−{b}+\left({a}+\mathrm{1}\right){i} \\ $$$$\mathrm{3}{a}−\mathrm{3}=−{b}\:\Rightarrow\mathrm{3}{a}+{b}=\mathrm{3} \\ $$$$\mathrm{3}{b}={a}+\mathrm{1}\:\Rightarrow{a}−\mathrm{3}{b}=−\mathrm{1} \\ $$$$\mathrm{9}{a}+\mathrm{3}{b}=\mathrm{9} \\ $$$$\Rightarrow{a}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\Rightarrow{b}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$
Commented by bemath last updated on 12/Aug/20
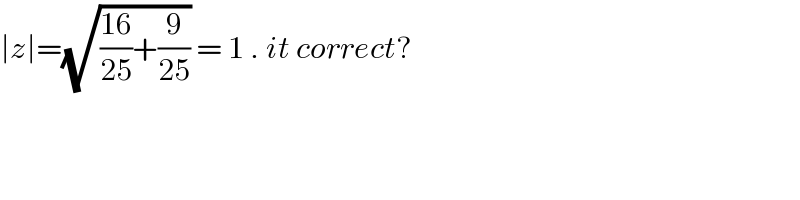
$$\mid{z}\mid=\sqrt{\frac{\mathrm{16}}{\mathrm{25}}+\frac{\mathrm{9}}{\mathrm{25}}}\:=\:\mathrm{1}\:.\:{it}\:{correct}?\: \\ $$
