
Question Number 107486 by bemath last updated on 11/Aug/20
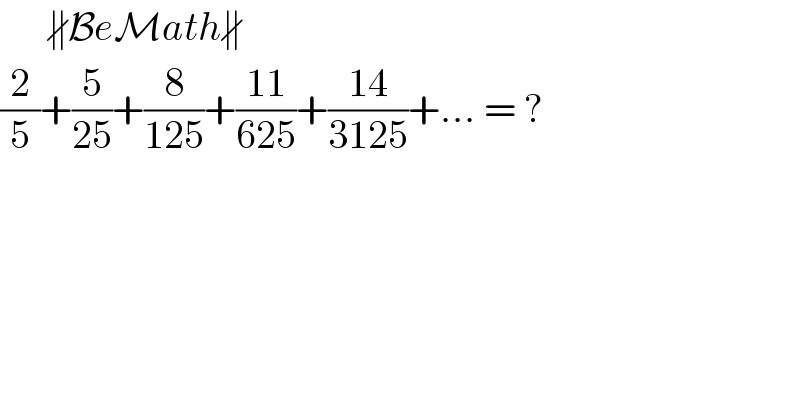
$$\:\:\:\:\:\:\nparallel\mathcal{B}{e}\mathcal{M}{ath}\nparallel \\ $$$$\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{5}}{\mathrm{25}}+\frac{\mathrm{8}}{\mathrm{125}}+\frac{\mathrm{11}}{\mathrm{625}}+\frac{\mathrm{14}}{\mathrm{3125}}+...\:=\:? \\ $$
Commented by bemath last updated on 11/Aug/20
$${thank}\:{you}\:{all}.\:{cooll}.. \\ $$
Answered by john santu last updated on 11/Aug/20
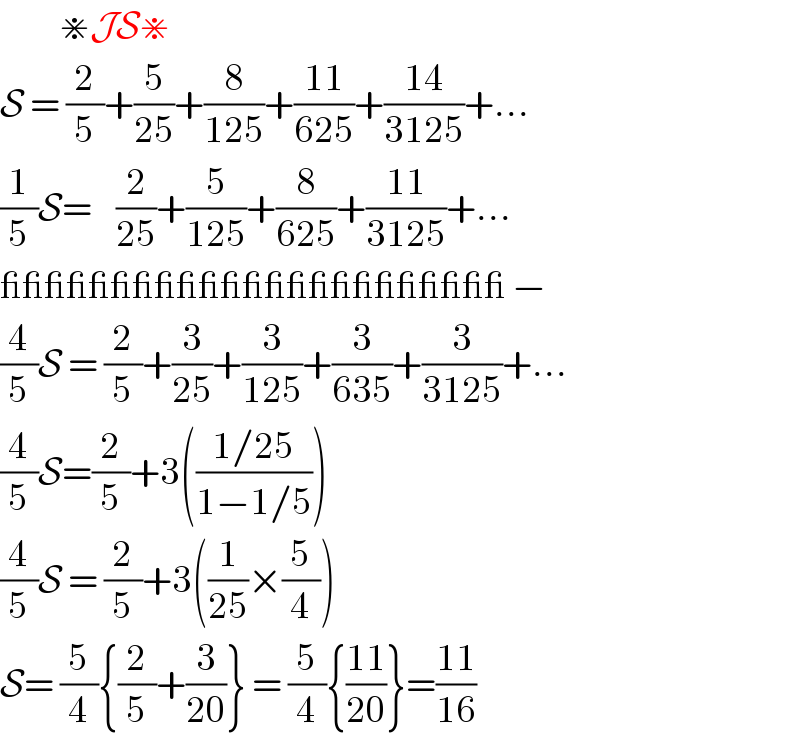
$$\:\:\:\:\:\:\:\:\:\:\divideontimes\mathcal{JS}\divideontimes \\ $$$$\mathcal{S}\:=\:\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{5}}{\mathrm{25}}+\frac{\mathrm{8}}{\mathrm{125}}+\frac{\mathrm{11}}{\mathrm{625}}+\frac{\mathrm{14}}{\mathrm{3125}}+... \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\mathcal{S}=\:\:\:\:\frac{\mathrm{2}}{\mathrm{25}}+\frac{\mathrm{5}}{\mathrm{125}}+\frac{\mathrm{8}}{\mathrm{625}}+\frac{\mathrm{11}}{\mathrm{3125}}+... \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\:− \\ $$$$\frac{\mathrm{4}}{\mathrm{5}}\mathcal{S}\:=\:\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{3}}{\mathrm{25}}+\frac{\mathrm{3}}{\mathrm{125}}+\frac{\mathrm{3}}{\mathrm{635}}+\frac{\mathrm{3}}{\mathrm{3125}}+... \\ $$$$\frac{\mathrm{4}}{\mathrm{5}}\mathcal{S}=\frac{\mathrm{2}}{\mathrm{5}}+\mathrm{3}\left(\frac{\mathrm{1}/\mathrm{25}}{\mathrm{1}−\mathrm{1}/\mathrm{5}}\right) \\ $$$$\frac{\mathrm{4}}{\mathrm{5}}\mathcal{S}\:=\:\frac{\mathrm{2}}{\mathrm{5}}+\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{25}}×\frac{\mathrm{5}}{\mathrm{4}}\right) \\ $$$$\mathcal{S}=\:\frac{\mathrm{5}}{\mathrm{4}}\left\{\frac{\mathrm{2}}{\mathrm{5}}+\frac{\mathrm{3}}{\mathrm{20}}\right\}\:=\:\frac{\mathrm{5}}{\mathrm{4}}\left\{\frac{\mathrm{11}}{\mathrm{20}}\right\}=\frac{\mathrm{11}}{\mathrm{16}} \\ $$
Answered by Dwaipayan Shikari last updated on 11/Aug/20

$${S}=\mathrm{2}{x}+\mathrm{5}{x}^{\mathrm{2}} +\mathrm{8}{x}^{\mathrm{3}} +\mathrm{11}{x}^{\mathrm{4}} +.....\:\:\:\:\left({x}=\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$$$−{xS}=\:\:−\mathrm{2}{x}^{\mathrm{2}} −\mathrm{5}{x}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{4}} −... \\ $$$${S}\left(\mathrm{1}−{x}\right)=\mathrm{2}{x}+\mathrm{3}\left({x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +...\right) \\ $$$${S}\left(\mathrm{1}−{x}\right)=\mathrm{2}{x}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{1}−{x}} \\ $$$${S}=\frac{\mathrm{2}{x}}{\mathrm{1}−{x}}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{16}}=\frac{\mathrm{11}}{\mathrm{16}}\:\:\left({x}=\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 11/Aug/20
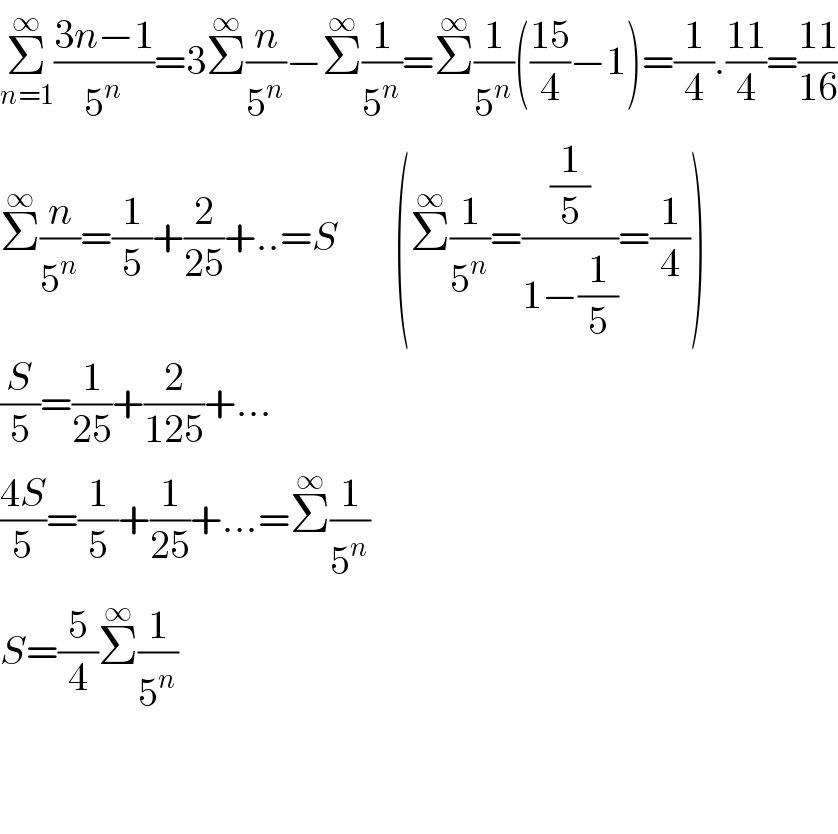
$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{3}{n}−\mathrm{1}}{\mathrm{5}^{{n}} }=\mathrm{3}\overset{\infty} {\sum}\frac{{n}}{\mathrm{5}^{{n}} }−\overset{\infty} {\sum}\frac{\mathrm{1}}{\mathrm{5}^{{n}} }=\overset{\infty} {\sum}\frac{\mathrm{1}}{\mathrm{5}^{{n}} }\left(\frac{\mathrm{15}}{\mathrm{4}}−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{4}}.\frac{\mathrm{11}}{\mathrm{4}}=\frac{\mathrm{11}}{\mathrm{16}} \\ $$$$\overset{\infty} {\sum}\frac{{n}}{\mathrm{5}^{{n}} }=\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{2}}{\mathrm{25}}+..={S}\:\:\:\:\:\:\:\left(\overset{\infty} {\sum}\frac{\mathrm{1}}{\mathrm{5}^{{n}} }=\frac{\frac{\mathrm{1}}{\mathrm{5}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}}=\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\frac{{S}}{\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{25}}+\frac{\mathrm{2}}{\mathrm{125}}+... \\ $$$$\frac{\mathrm{4}{S}}{\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{25}}+...=\overset{\infty} {\sum}\frac{\mathrm{1}}{\mathrm{5}^{{n}} } \\ $$$${S}=\frac{\mathrm{5}}{\mathrm{4}}\overset{\infty} {\sum}\frac{\mathrm{1}}{\mathrm{5}^{{n}} } \\ $$$$ \\ $$$$ \\ $$
