
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 173976 by savitar last updated on 22/Jul/22
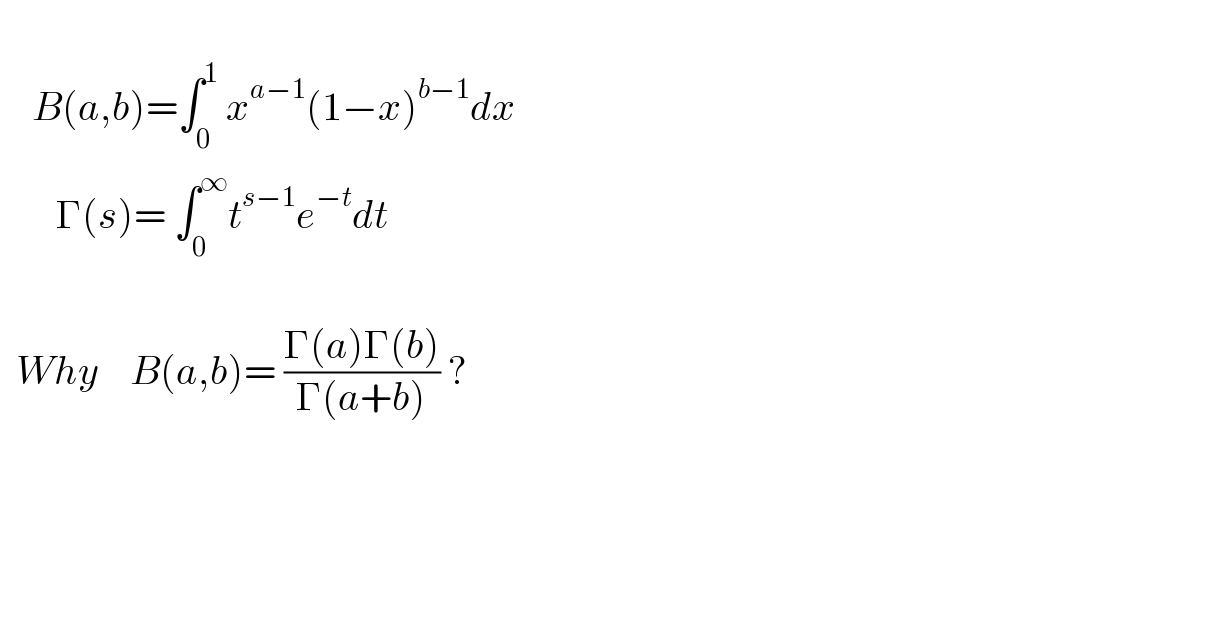
$$ \\ $$$$\:\:\:\:{B}\left({a},{b}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{a}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{b}−\mathrm{1}} {dx}\: \\ $$$$\:\:\:\:\:\:\:\Gamma\left({s}\right)=\:\int_{\mathrm{0}} ^{\infty} {t}^{{s}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$ \\ $$$$\:\:{Why}\:\:\:\:{B}\left({a},{b}\right)=\:\frac{\Gamma\left({a}\right)\Gamma\left({b}\right)}{\Gamma\left({a}+{b}\right)}\:? \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by aleks041103 last updated on 22/Jul/22
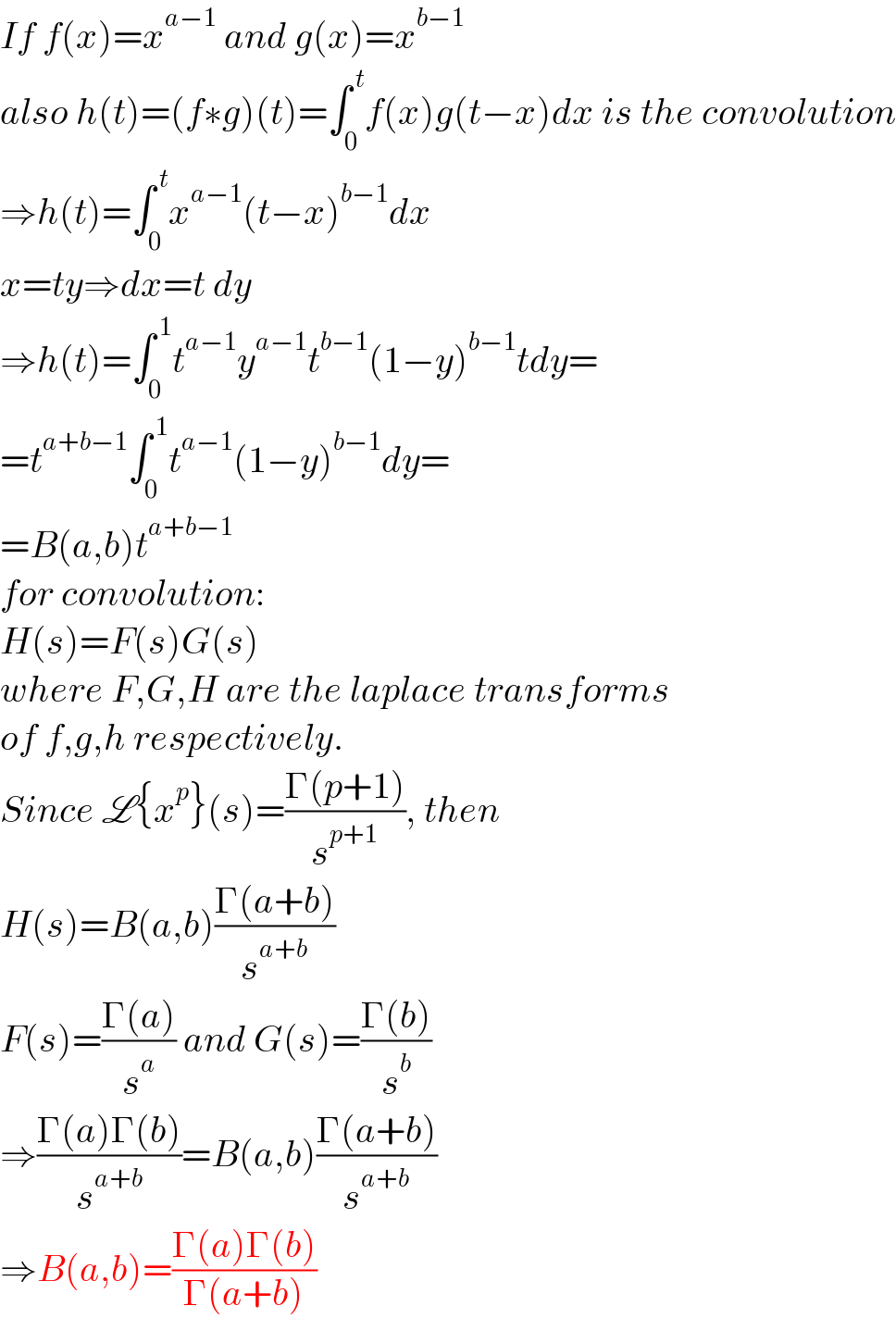
$${If}\:{f}\left({x}\right)={x}^{{a}−\mathrm{1}} \:{and}\:{g}\left({x}\right)={x}^{{b}−\mathrm{1}} \\ $$$${also}\:{h}\left({t}\right)=\left({f}\ast{g}\right)\left({t}\right)=\int_{\mathrm{0}} ^{\:{t}} {f}\left({x}\right){g}\left({t}−{x}\right){dx}\:{is}\:{the}\:{convolution} \\ $$$$\Rightarrow{h}\left({t}\right)=\int_{\mathrm{0}} ^{\:{t}} {x}^{{a}−\mathrm{1}} \left({t}−{x}\right)^{{b}−\mathrm{1}} {dx} \\ $$$${x}={ty}\Rightarrow{dx}={t}\:{dy} \\ $$$$\Rightarrow{h}\left({t}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} {t}^{{a}−\mathrm{1}} {y}^{{a}−\mathrm{1}} {t}^{{b}−\mathrm{1}} \left(\mathrm{1}−{y}\right)^{{b}−\mathrm{1}} {tdy}= \\ $$$$={t}^{{a}+{b}−\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} {t}^{{a}−\mathrm{1}} \left(\mathrm{1}−{y}\right)^{{b}−\mathrm{1}} {dy}= \\ $$$$={B}\left({a},{b}\right){t}^{{a}+{b}−\mathrm{1}} \\ $$$${for}\:{convolution}: \\ $$$${H}\left({s}\right)={F}\left({s}\right){G}\left({s}\right) \\ $$$${where}\:{F},{G},{H}\:{are}\:{the}\:{laplace}\:{transforms} \\ $$$${of}\:{f},{g},{h}\:{respectively}. \\ $$$${Since}\:\mathscr{L}\left\{{x}^{{p}} \right\}\left({s}\right)=\frac{\Gamma\left({p}+\mathrm{1}\right)}{{s}^{{p}+\mathrm{1}} },\:{then} \\ $$$${H}\left({s}\right)={B}\left({a},{b}\right)\frac{\Gamma\left({a}+{b}\right)}{{s}^{{a}+{b}} } \\ $$$${F}\left({s}\right)=\frac{\Gamma\left({a}\right)}{{s}^{{a}} }\:{and}\:{G}\left({s}\right)=\frac{\Gamma\left({b}\right)}{{s}^{{b}} } \\ $$$$\Rightarrow\frac{\Gamma\left({a}\right)\Gamma\left({b}\right)}{{s}^{{a}+{b}} }={B}\left({a},{b}\right)\frac{\Gamma\left({a}+{b}\right)}{{s}^{{a}+{b}} } \\ $$$$\Rightarrow{B}\left({a},{b}\right)=\frac{\Gamma\left({a}\right)\Gamma\left({b}\right)}{\Gamma\left({a}+{b}\right)} \\ $$
Commented by savitar last updated on 22/Jul/22

$${Very}\:{nice}\:{sir} \\ $$
