
Question Number 199183 by hardmath last updated on 29/Oct/23
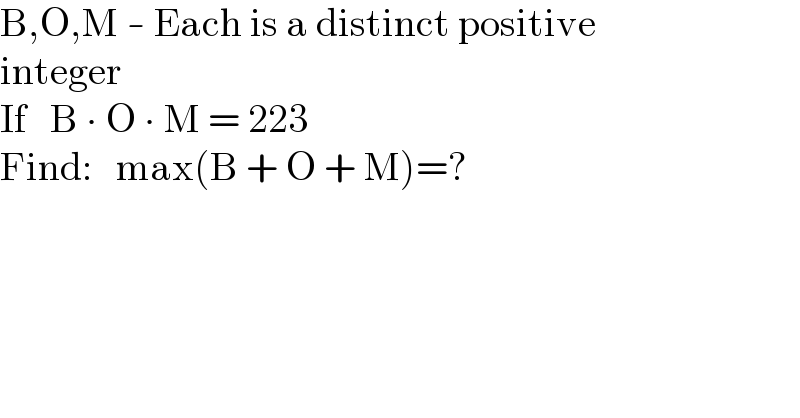
$$\mathrm{B},\mathrm{O},\mathrm{M}\:-\:\mathrm{Each}\:\mathrm{is}\:\mathrm{a}\:\mathrm{distinct}\:\mathrm{positive} \\ $$$$\mathrm{integer} \\ $$$$\mathrm{If}\:\:\:\mathrm{B}\:\centerdot\:\mathrm{O}\:\centerdot\:\mathrm{M}\:=\:\mathrm{223} \\ $$$$\mathrm{Find}:\:\:\:\mathrm{max}\left(\mathrm{B}\:+\:\mathrm{O}\:+\:\mathrm{M}\right)=? \\ $$
Answered by mr W last updated on 19/Nov/23
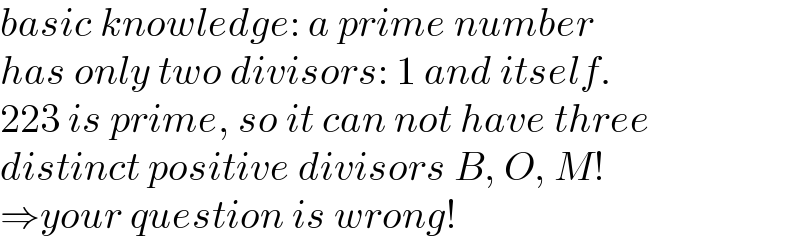
$${basic}\:{knowledge}:\:{a}\:{prime}\:{number} \\ $$$${has}\:{only}\:{two}\:{divisors}:\:\mathrm{1}\:{and}\:{itself}. \\ $$$$\mathrm{223}\:{is}\:{prime},\:{so}\:{it}\:{can}\:{not}\:{have}\:{three} \\ $$$${distinct}\:{positive}\:{divisors}\:{B},\:{O},\:{M}! \\ $$$$\Rightarrow{your}\:{question}\:{is}\:{wrong}! \\ $$
