
Question Number 201660 by LimPorly last updated on 10/Dec/23

$${An}\:{equilateral}\:{triangle}\:{inscribed}\:{in}\:{a}\:{parabola} \\ $$$${y}^{\mathrm{2}} =\mathrm{4}{x}.\:{One}\:{of}\:{its}\:{vertices}\:{is}\:{at}\:{the}\:{vertex}\:{of}\:\:{the}\:{parabola}. \\ $$$${Find}\:{the}\:{length}\:{of}\:{each}\:{side}\:{of}\:{the}\:{triangle}\:{in}\:{units}. \\ $$
Answered by som(math1967) last updated on 10/Dec/23
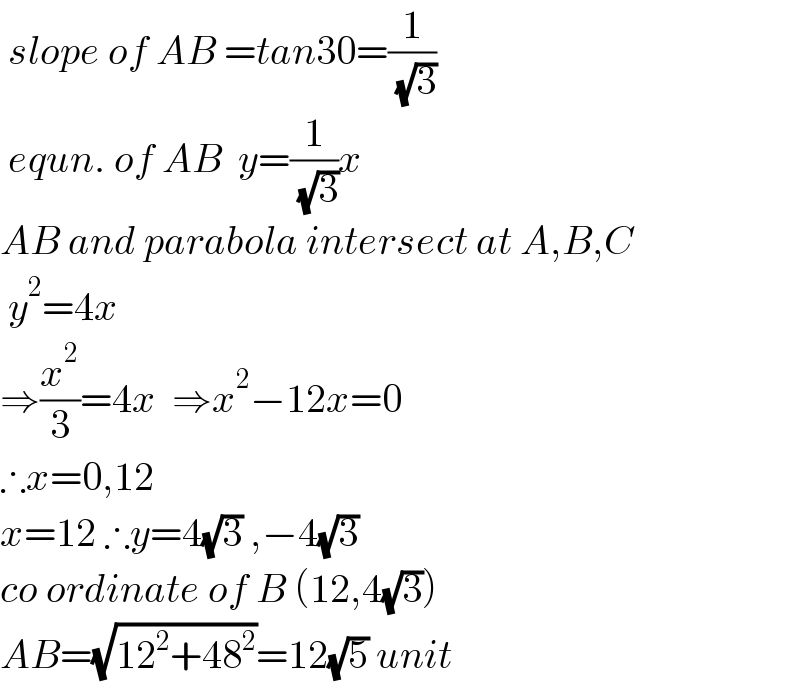
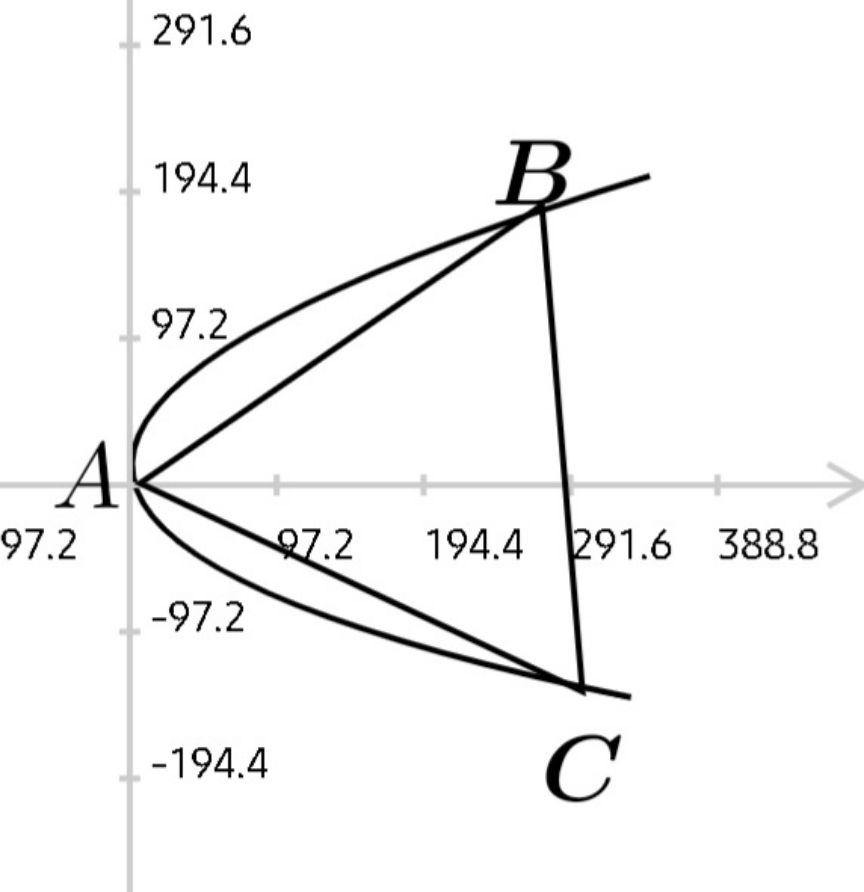
$$\:{slope}\:{of}\:{AB}\:={tan}\mathrm{30}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\:{equn}.\:{of}\:{AB}\:\:{y}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{x} \\ $$$${AB}\:{and}\:{parabola}\:{intersect}\:{at}\:{A},{B},{C} \\ $$$$\:{y}^{\mathrm{2}} =\mathrm{4}{x} \\ $$$$\Rightarrow\frac{{x}^{\mathrm{2}} }{\mathrm{3}}=\mathrm{4}{x}\:\:\Rightarrow{x}^{\mathrm{2}} −\mathrm{12}{x}=\mathrm{0} \\ $$$$\therefore{x}=\mathrm{0},\mathrm{12} \\ $$$${x}=\mathrm{12}\:\therefore{y}=\mathrm{4}\sqrt{\mathrm{3}}\:,−\mathrm{4}\sqrt{\mathrm{3}} \\ $$$${co}\:{ordinate}\:{of}\:{B}\:\left(\mathrm{12},\mathrm{4}\sqrt{\mathrm{3}}\right) \\ $$$${AB}=\sqrt{\mathrm{12}^{\mathrm{2}} +\mathrm{48}^{\mathrm{2}} }=\mathrm{12}\sqrt{\mathrm{5}}\:{unit} \\ $$
Commented by som(math1967) last updated on 10/Dec/23
Commented by LimPorly last updated on 10/Dec/23

$${Thank}\:{a}\:{lot}\:{sir} \\ $$
