
AllQuestion and Answers: Page 995
Question Number 121199 Answers: 0 Comments: 0

Question Number 121188 Answers: 0 Comments: 0
Question Number 121175 Answers: 1 Comments: 0

Question Number 121174 Answers: 4 Comments: 0
Question Number 121172 Answers: 2 Comments: 0
Question Number 121170 Answers: 0 Comments: 0
Question Number 121154 Answers: 4 Comments: 0

Question Number 121152 Answers: 0 Comments: 0

Question Number 121138 Answers: 2 Comments: 0

Question Number 121136 Answers: 2 Comments: 1

Question Number 121134 Answers: 2 Comments: 0
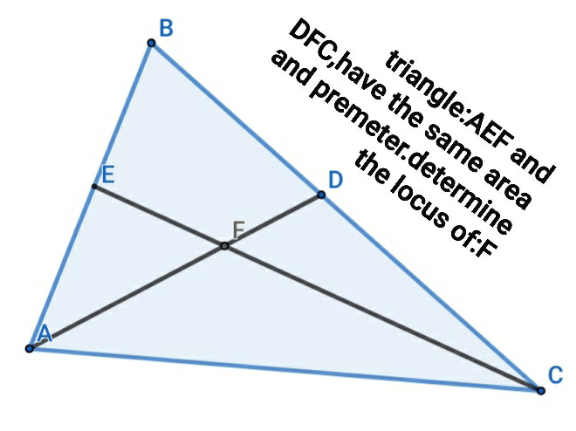
Question Number 121127 Answers: 3 Comments: 0
Question Number 121123 Answers: 1 Comments: 0
Question Number 121119 Answers: 4 Comments: 0
Question Number 121117 Answers: 2 Comments: 0
Question Number 121111 Answers: 0 Comments: 7

Question Number 121102 Answers: 2 Comments: 0
Question Number 121100 Answers: 1 Comments: 0

Question Number 121099 Answers: 1 Comments: 0
Question Number 121097 Answers: 1 Comments: 0

Question Number 121092 Answers: 0 Comments: 0

Question Number 121091 Answers: 0 Comments: 1

Question Number 121085 Answers: 3 Comments: 1

Question Number 121081 Answers: 0 Comments: 1
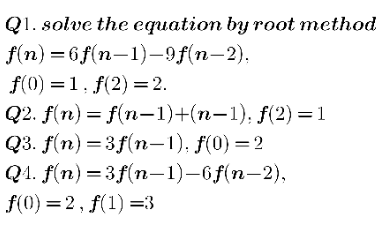
Question Number 121077 Answers: 5 Comments: 1

Question Number 121074 Answers: 2 Comments: 0
Pg 990 Pg 991 Pg 992 Pg 993 Pg 994 Pg 995 Pg 996 Pg 997 Pg 998 Pg 999
