Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 994

Question Number 120905 Answers: 4 Comments: 0

y′ = xy^2 −(y/x)

$$\:\:\mathrm{y}'\:=\:\mathrm{xy}^{\mathrm{2}} −\frac{\mathrm{y}}{\mathrm{x}} \\ $$

Question Number 120904 Answers: 1 Comments: 1

Question Number 120996 Answers: 0 Comments: 0

Question Number 120895 Answers: 1 Comments: 3

Question Number 120898 Answers: 0 Comments: 0

evaluate: ∫_0 ^( ∞) ((x/(x+1)) − lim_(k→∞) ((k/(k+1)))^(⌊k⌋) )^(⌊x⌋) dx

$$\: \\ $$$$\: \\ $$$$\: \\ $$$$\mathrm{evaluate}:\:\int_{\mathrm{0}} ^{\:\infty} \left(\frac{{x}}{{x}+\mathrm{1}}\:−\:\underset{{k}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{{k}}{{k}+\mathrm{1}}\right)^{\lfloor{k}\rfloor} \right)^{\lfloor{x}\rfloor} {dx} \\ $$$$\: \\ $$$$\: \\ $$

Question Number 120882 Answers: 1 Comments: 0

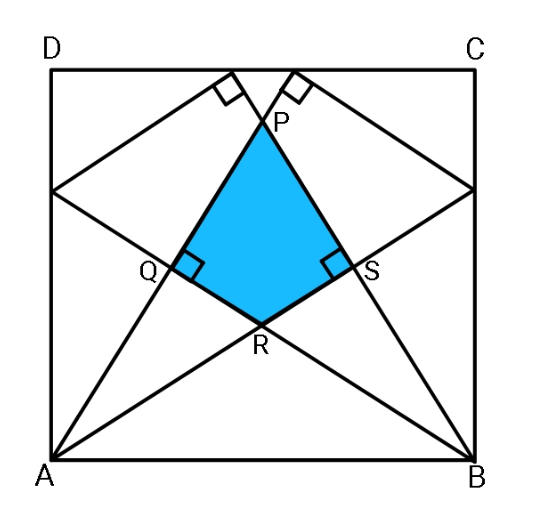
Question Number 120879 Answers: 0 Comments: 0

Question Number 120875 Answers: 0 Comments: 0

... Nice calculus... evaluate :: S= Σ_(n=1) ^∞ ((2^(−2n) /(1+cos((π/2^n )))))=?? ...M.N.1970...

$$\:\:\:\:\:\:\:\:\:\:...\:\mathscr{N}{ice}\:{calculus}... \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\:\:\:\:{S}=\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{2}^{−\mathrm{2}{n}} }{\mathrm{1}+{cos}\left(\frac{\pi}{\mathrm{2}^{{n}} }\right)}\right)=??\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...\mathscr{M}.\mathscr{N}.\mathrm{1970}... \\ $$

Question Number 120869 Answers: 0 Comments: 0

Question Number 120868 Answers: 0 Comments: 0

Question Number 120864 Answers: 1 Comments: 3

Question Number 120862 Answers: 1 Comments: 1

lim_(x→∞) ((sin^2 ((2/x))−cos ((1/x))+1)/(sec ((3/x)) tan^2 ((3/x)))) ?

$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{sin}\:^{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{x}}\right)−\mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)+\mathrm{1}}{\mathrm{sec}\:\left(\frac{\mathrm{3}}{\mathrm{x}}\right)\:\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{x}}\right)}\:? \\ $$

Question Number 120855 Answers: 2 Comments: 0

... elementary calculus... :: α,β are roots of equation of : x^2 −6x−2=0 define :: t_n =α^n −β^n (n≥1) then evaluate : A=((t_(10) −2t_8 )/(2t_9 )) =??? ...m.n.1970...

$$\:\:\:\:\:\:\:\:\:\:\:...\:{elementary}\:\:{calculus}... \\ $$$$\:\:::\:\alpha,\beta\:{are}\:{roots}\:{of}\:\:{equation} \\ $$$$\:\:\:\:\:{of}\::\:{x}^{\mathrm{2}} −\mathrm{6}{x}−\mathrm{2}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:{define}\:::\:{t}_{{n}} =\alpha^{{n}} −\beta^{{n}} \:\left({n}\geqslant\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{then}\:\:{evaluate}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{A}=\frac{{t}_{\mathrm{10}} −\mathrm{2}{t}_{\mathrm{8}} }{\mathrm{2}{t}_{\mathrm{9}} }\:=??? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{m}.{n}.\mathrm{1970}... \\ $$

Question Number 120847 Answers: 0 Comments: 1

If x,y,z then prove the following inequality (x^2 +2)(y^2 +2)(z^2 +2)=9(xy+yz+xz)

$${If}\:{x},{y},{z}\:\:{then}\:{prove}\:{the}\:{following} \\ $$$${inequality} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{2}\right)\left({y}^{\mathrm{2}} +\mathrm{2}\right)\left({z}^{\mathrm{2}} +\mathrm{2}\right)=\mathrm{9}\left({xy}+{yz}+{xz}\right) \\ $$

Question Number 120843 Answers: 1 Comments: 1

lim_(x→3) ((√(x+9−6(√x)))/( (√x)−3)) ?

$$\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{x}+\mathrm{9}−\mathrm{6}\sqrt{\mathrm{x}}}}{\:\sqrt{\mathrm{x}}−\mathrm{3}}\:? \\ $$

Question Number 120839 Answers: 3 Comments: 0

Question Number 120827 Answers: 4 Comments: 4

Question Number 120823 Answers: 1 Comments: 0

Question Number 120819 Answers: 0 Comments: 3

If f(x) +2f((1/x)) +3f((x/(x−1))) = x what is f(x) ?

$$\mathrm{If}\:\mathrm{f}\left(\mathrm{x}\right)\:+\mathrm{2f}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:+\mathrm{3f}\left(\frac{\mathrm{x}}{\mathrm{x}−\mathrm{1}}\right)\:=\:\mathrm{x}\: \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{f}\left(\mathrm{x}\right)\:? \\ $$

Question Number 120812 Answers: 1 Comments: 0

Find all integral solutions to the equation (x^2 +1)(y^2 +1)+2(x−y)(1−xy)=4(1+xy)

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{integral}\:\mathrm{solutions}\:\mathrm{to}\: \\ $$$$\mathrm{the}\:\mathrm{equation}\:\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{2}\left(\mathrm{x}−\mathrm{y}\right)\left(\mathrm{1}−\mathrm{xy}\right)=\mathrm{4}\left(\mathrm{1}+\mathrm{xy}\right) \\ $$

Question Number 120811 Answers: 1 Comments: 0

Find the singular point in the differential equation : (x^3 − x^2 − 9x + 9)(d^2 y/dx^2 ) +2x(dy/dx) + (x − 3)y = 0

$${Find}\:{the}\:{singular}\:{point}\:{in}\:{the} \\ $$$${differential}\:{equation}\:: \\ $$$$ \\ $$$$\left({x}^{\mathrm{3}} \:−\:{x}^{\mathrm{2}} \:−\:\mathrm{9}{x}\:+\:\mathrm{9}\right)\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\mathrm{2}{x}\frac{{dy}}{{dx}}\:+\:\left({x}\:−\:\mathrm{3}\right){y}\:=\:\mathrm{0} \\ $$

Question Number 120810 Answers: 1 Comments: 0

Determine the convergence intervval of : Σ_(n = 0) ^∞ (−1)^n (x − 1)^n

$${Determine}\:{the}\:{convergence}\:{intervval}\:{of}\:: \\ $$$$\underset{{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \:\left({x}\:−\:\mathrm{1}\right)^{{n}} \\ $$

Question Number 120809 Answers: 0 Comments: 0

Find the largest number of positive integers that can be found in such a way that any two of them a and b ( a≠b) satisfy the next inequality ∣a−b∣≥((ab)/(100))

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{largest}\:\mathrm{number}\:\mathrm{of}\:\mathrm{positive} \\ $$$$\mathrm{integers}\:\mathrm{that}\:\mathrm{can}\:\mathrm{be}\:\mathrm{found}\:\mathrm{in}\:\mathrm{such}\:\mathrm{a}\:\mathrm{way} \\ $$$$\mathrm{that}\:\mathrm{any}\:\mathrm{two}\:\mathrm{of}\:\mathrm{them}\:{a}\:\mathrm{and}\:{b}\:\left(\:{a}\neq{b}\right)\: \\ $$$$\mathrm{satisfy}\:\mathrm{the}\:\mathrm{next}\:\mathrm{inequality}\:\mid{a}−{b}\mid\geqslant\frac{{ab}}{\mathrm{100}} \\ $$

Question Number 120801 Answers: 1 Comments: 2

Question Number 120800 Answers: 0 Comments: 1

what remain when we divise 2222^(3333 ) by 3333^(2222)

$${what}\:{remain}\:{when}\:{we}\:{divise} \\ $$$$\mathrm{2222}^{\mathrm{3333}\:} {by}\:\mathrm{3333}^{\mathrm{2222}} \\ $$

Question Number 120797 Answers: 0 Comments: 1

Pg 989 Pg 990 Pg 991 Pg 992 Pg 993 Pg 994 Pg 995 Pg 996 Pg 997 Pg 998

Contact: info@tinkutara.com