Question and Answers Forum

AllQuestion and Answers: Page 918

Question Number 127060 Answers: 0 Comments: 0

Question Number 127056 Answers: 1 Comments: 0

Question Number 127045 Answers: 2 Comments: 0

((cos 1°+cos 2°+cos 3°+...+cos 44°)/(sin 1°+sin 2°+sin 3°+...+sin 44°)) =?

$$\:\:\frac{\mathrm{cos}\:\mathrm{1}°+\mathrm{cos}\:\mathrm{2}°+\mathrm{cos}\:\mathrm{3}°+...+\mathrm{cos}\:\mathrm{44}°}{\mathrm{sin}\:\mathrm{1}°+\mathrm{sin}\:\mathrm{2}°+\mathrm{sin}\:\mathrm{3}°+...+\mathrm{sin}\:\mathrm{44}°}\:=? \\ $$

Question Number 127042 Answers: 2 Comments: 1

∫_(1/(√2)) ^( 1) ((arcsin x)/x^3 ) dx ? ′ not nice integral ′

$$\:\int_{\mathrm{1}/\sqrt{\mathrm{2}}} ^{\:\mathrm{1}} \frac{\mathrm{arcsin}\:{x}}{{x}^{\mathrm{3}} }\:{dx}\:? \\ $$$$\:'\:{not}\:{nice}\:{integral}\:'\: \\ $$

Question Number 127080 Answers: 0 Comments: 1

Σ_(n=1) ^∞ (1/(e^(−φn) +((e^(2πn) −e^(−2φn) )/(2e^(−φn) +((e^(2πn) −e^(−2φn) )/(2e^(−φn) +((e^(2πn) −e^(−2φn) )/(2e^(−2φn) ...))))))))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{e}^{−\phi{n}} +\frac{{e}^{\mathrm{2}\pi{n}} −{e}^{−\mathrm{2}\phi{n}} \:}{\mathrm{2}{e}^{−\phi{n}} +\frac{{e}^{\mathrm{2}\pi{n}} −{e}^{−\mathrm{2}\phi{n}} }{\mathrm{2}{e}^{−\phi{n}} +\frac{{e}^{\mathrm{2}\pi{n}} −{e}^{−\mathrm{2}\phi{n}} }{\mathrm{2}{e}^{−\mathrm{2}\phi{n}} ...}}}} \\ $$

Question Number 127032 Answers: 2 Comments: 0

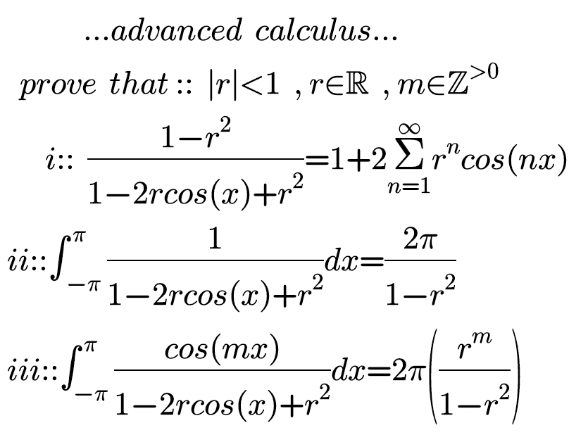
Question Number 127047 Answers: 2 Comments: 0

how can graph this [x^2 +(y−1)^2 >9 ] pleas sir help me with details ?

$${how}\:{can}\:{graph}\:{this}\: \\ $$$$\left[{x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{9}\:\right]\:{pleas}\:{sir}\:{help}\:{me}\:{with}\:{details}\:? \\ $$

Question Number 127020 Answers: 3 Comments: 1

super nice ! show that ζ(6) = (π^6 /(945))

$$\:\:{super}\:{nice}\:! \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{show}\:{that}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\zeta\left(\mathrm{6}\right)\:=\:\frac{\pi^{\mathrm{6}} }{\mathrm{945}} \\ $$

Question Number 127018 Answers: 1 Comments: 0

Vf×2=Vi×2+2aΔd 0=16.5

$${Vf}×\mathrm{2}={Vi}×\mathrm{2}+\mathrm{2}{a}\Delta{d} \\ $$$$\mathrm{0}=\mathrm{16}.\mathrm{5} \\ $$

Question Number 127017 Answers: 2 Comments: 0

...NICE CALCULUS... prove that :: ∫_0 ^( ∞) (((x^2 ln(πx))/π^(πx) ))dx =(1/((πln(π))^3 ))[(3−2(γ+ln(ln(π)))]

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:...{NICE}\:\:\:\:\:{CALCULUS}... \\ $$$$\:\:{prove}\:{that}\::: \\ $$$$\int_{\mathrm{0}} ^{\:\infty} \:\left(\frac{{x}^{\mathrm{2}} {ln}\left(\pi{x}\right)}{\pi^{\pi{x}} }\right){dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\left(\pi{ln}\left(\pi\right)\right)^{\mathrm{3}} }\left[\left(\mathrm{3}−\mathrm{2}\left(\gamma+{ln}\left({ln}\left(\pi\right)\right)\right)\right]\right. \\ $$

Question Number 127012 Answers: 1 Comments: 0

Question Number 127009 Answers: 1 Comments: 0

f(x,y)={((2x(x^2 −y^2 ))/(x^2 +y^2 )) ,(x,y)≠(0,0) {0 ,(x,y)=(0,0) check continuity

$${f}\left({x},{y}\right)=\left\{\frac{\mathrm{2}{x}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\:\:\:,\left({x},{y}\right)\neq\left(\mathrm{0},\mathrm{0}\right)\right. \\ $$$$\left\{\mathrm{0}\:\:\:\:,\left({x},{y}\right)=\left(\mathrm{0},\mathrm{0}\right)\right. \\ $$$${check}\:{continuity} \\ $$

Question Number 127006 Answers: 1 Comments: 0

Two pipes A and B together can fill a cistern in 5 hours. Had they been opened separately, then B would have taken 6 hours more than A to fill the cistern. How much time will be taken by A to fill the cistern separately?

$${Two}\:{pipes}\:{A}\:{and}\:{B}\:{together}\:{can}\:{fill}\: \\ $$$${a}\:{cistern}\:{in}\:\mathrm{5}\:{hours}.\:{Had}\:{they}\:{been}\:{opened} \\ $$$${separately},\:{then}\:{B}\:{would}\:{have}\:{taken}\: \\ $$$$\mathrm{6}\:{hours}\:{more}\:{than}\:{A}\:{to}\:{fill}\:{the}\:{cistern}. \\ $$$${How}\:{much}\:{time}\:{will}\:{be}\:{taken}\:{by}\:{A}\:{to}\:{fill} \\ $$$${the}\:{cistern}\:{separately}?\: \\ $$

Question Number 127004 Answers: 0 Comments: 1

Question Number 127002 Answers: 1 Comments: 1

lim_(x→0) ((2+cos (3x)−3csch (x))/(ln (1+x^2 ))) =?

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}+\mathrm{cos}\:\left(\mathrm{3}{x}\right)−\mathrm{3csch}\:\left({x}\right)}{\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:=? \\ $$

Question Number 126997 Answers: 1 Comments: 0

∫_0 ^1 arcsin (((sin x)/( (√2)))) dx =?

$$\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{arcsin}\:\left(\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{2}}}\right)\:{dx}\:=? \\ $$

Question Number 126994 Answers: 1 Comments: 0

∫ (x^4 /(1+x^8 )) dx =?

$$\:\int\:\frac{{x}^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{8}} }\:{dx}\:=? \\ $$

Question Number 126992 Answers: 0 Comments: 2

App Information: We have unpublished free versoon of the app from playstore. Existing users can still see the app on playstore. A paid version will soon be available. We will update pinned message once it is available. Thank You.

$$\mathrm{App}\:\mathrm{Information}: \\ $$$$\mathrm{We}\:\mathrm{have}\:\mathrm{unpublished}\:\mathrm{free}\:\mathrm{versoon} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{app}\:\mathrm{from}\:\mathrm{playstore}. \\ $$$$\mathrm{Existing}\:\mathrm{users}\:\mathrm{can}\:\mathrm{still}\:\mathrm{see}\:\mathrm{the} \\ $$$$\mathrm{app}\:\mathrm{on}\:\mathrm{playstore}. \\ $$$$\mathrm{A}\:\mathrm{paid}\:\mathrm{version}\:\mathrm{will}\:\mathrm{soon}\:\mathrm{be}\:\mathrm{available}. \\ $$$$\mathrm{We}\:\mathrm{will}\:\mathrm{update}\:\mathrm{pinned}\:\mathrm{message}\:\mathrm{once} \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{available}. \\ $$$$\mathrm{Thank}\:\mathrm{You}. \\ $$

Question Number 126990 Answers: 1 Comments: 0

Obtain a formula for I_n = ∫_0 ^n [x] dx in terms of n where [x] is the greatest integer function of x.

$$\mathrm{Obtain}\:\mathrm{a}\:\mathrm{formula}\:\mathrm{for}\: \\ $$$$\:{I}_{{n}} \:=\:\underset{\mathrm{0}} {\overset{{n}} {\int}}\left[{x}\right]\:{dx}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:{n} \\ $$$$\:\mathrm{where}\:\left[{x}\right]\:\mathrm{is}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{integer}\:\mathrm{function}\:\mathrm{of}\:{x}. \\ $$

Question Number 126989 Answers: 1 Comments: 0

∫e^(√x) dx

$$\int{e}^{\sqrt{{x}}} {dx} \\ $$

Question Number 126987 Answers: 1 Comments: 0