Question and Answers Forum

AllQuestion and Answers: Page 770

Question Number 141916 Answers: 1 Comments: 0

prove that:: I:=∫_0 ^( (π/2)) arccosh(sin(x)+cos(x))dx=(π/2)ln(2) ..

$$ \\ $$$$\:\:\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\mathrm{I}:=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {arccosh}\left({sin}\left({x}\right)+{cos}\left({x}\right)\right){dx}=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:.. \\ $$

Question Number 141914 Answers: 3 Comments: 0

prove that:: φ:=∫_0 ^( π) (x/((sin(x))^(1/2) ))dx=(√(π/8)) Γ^( 2) ((1/4))...✓ .........

$$\:\:\:\: \\ $$$$\:\:\:\:\:\:{prove}\:{that}:: \\ $$$$\:\:\:\:\:\phi:=\int_{\mathrm{0}} ^{\:\pi} \frac{{x}}{\left({sin}\left({x}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{dx}=\sqrt{\frac{\pi}{\mathrm{8}}}\:\Gamma^{\:\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)...\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:......... \\ $$

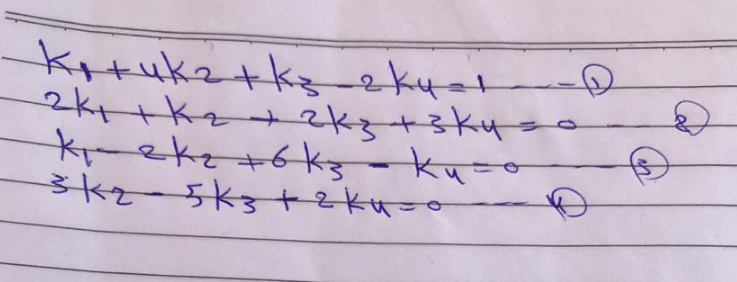
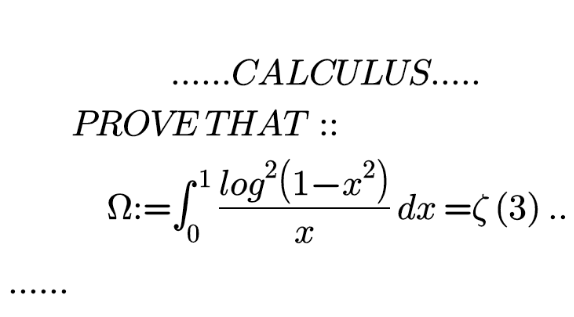
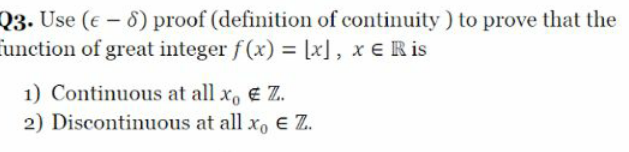
Question Number 141912 Answers: 0 Comments: 0

Q138579

$${Q}\mathrm{138579} \\ $$

Question Number 141911 Answers: 0 Comments: 0

Q137956

$${Q}\mathrm{137956} \\ $$

Question Number 141910 Answers: 0 Comments: 0

Q137026

$${Q}\mathrm{137026} \\ $$

Question Number 141909 Answers: 1 Comments: 1

Question Number 141908 Answers: 0 Comments: 0

Q137984

$${Q}\mathrm{137984} \\ $$$$ \\ $$

Question Number 141907 Answers: 0 Comments: 0

Q140000

$${Q}\mathrm{140000} \\ $$

Question Number 141905 Answers: 0 Comments: 0

Q137503

$${Q}\mathrm{137503} \\ $$

Question Number 141901 Answers: 0 Comments: 1

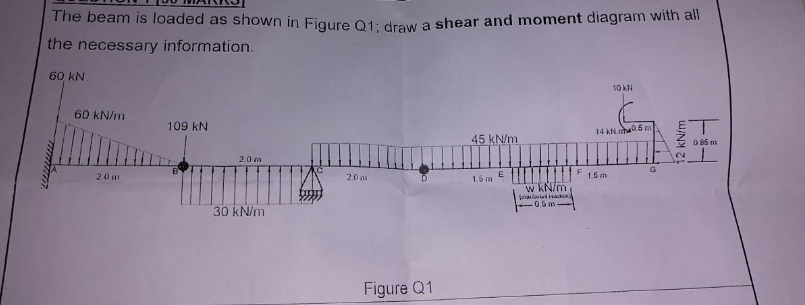
Question Number 141900 Answers: 2 Comments: 0

L = lim_(x→0) ((e^x cos x−x−1)/x^3 ) =?

$$\:\mathcal{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}} \:\mathrm{cos}\:{x}−{x}−\mathrm{1}}{{x}^{\mathrm{3}} }\:=? \\ $$

Question Number 141890 Answers: 0 Comments: 1

Question Number 141885 Answers: 3 Comments: 0

easy question: if lim_(x→0) ((1−cos(1−cos(1−cos(x))))/x^8 ) =2^( a) then a=??

$$\:\:\: \\ $$$$\:\:\:\:\:\:{easy}\:\:{question}: \\ $$$$\:\:\:\:{if}\:\:\:{lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−{cos}\left(\mathrm{1}−{cos}\left(\mathrm{1}−{cos}\left({x}\right)\right)\right)}{{x}^{\mathrm{8}} }\:=\mathrm{2}^{\:{a}} \\ $$$$\:\:\:\:\:\:\:\:{then}\:\:\:{a}=??\:\: \\ $$

Question Number 141884 Answers: 0 Comments: 0

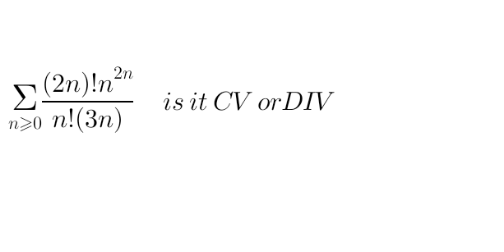
Question Number 141868 Answers: 1 Comments: 1

......Advanced .....Calculus........ ..... ∫_( R) ^ (e^(−x^2 ) /((1+x^2 )^2 )) dx=?

$$\:\:\:\:\:\:\:\:\:\:\:\:......\mathscr{A}{dvanced}\:\:.....\mathscr{C}{alculus}........ \\ $$$$\:\:\:\:\:\:\:\:\:.....\:\:\int_{\:\mathbb{R}} ^{\:} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}=? \\ $$$$\:\:\:\:\: \\ $$

Question Number 141859 Answers: 2 Comments: 1

∫_0 ^∞ ((4e^(−x^2 ) )/((2x^2 +1)^2 )) dx

$$\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{4}{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\: \\ $$

Question Number 141858 Answers: 1 Comments: 1

Question Number 141872 Answers: 1 Comments: 2

Question Number 141849 Answers: 1 Comments: 0

y′′−6y′+9y = 9x^2 e^(3x) cos (3x)

$$\:\:\:\:\:{y}''−\mathrm{6}{y}'+\mathrm{9}{y}\:=\:\mathrm{9}{x}^{\mathrm{2}} \:{e}^{\mathrm{3}{x}} \:\mathrm{cos}\:\left(\mathrm{3}{x}\right)\:\: \\ $$

Question Number 141848 Answers: 4 Comments: 0

I = ∫ (1/( (√(1−x^2 ))−1)) dx

$$\:\mathscr{I}\:=\:\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1}}\:{dx}\: \\ $$

Question Number 141847 Answers: 2 Comments: 0

I = ∫ ((sec x)/(1+csc x)) dx

$$\:\mathcal{I}\:=\:\int\:\frac{\mathrm{sec}\:{x}}{\mathrm{1}+\mathrm{csc}\:{x}}\:{dx}\: \\ $$

Question Number 141846 Answers: 1 Comments: 0

Σ_(k≥0) (C_n ^k )^2

$$\sum_{{k}\geqslant\mathrm{0}} \left({C}_{{n}} ^{{k}} \right)^{\mathrm{2}} \\ $$

Question Number 142174 Answers: 0 Comments: 6

Question Number 141840 Answers: 0 Comments: 0

sin^2 (360−x)−((cos(x−180)∙tan(−x)∙sin(90−x)∙cos(360−x))/(sin(180−x)))=?

$${sin}^{\mathrm{2}} \left(\mathrm{360}−{x}\right)−\frac{{cos}\left({x}−\mathrm{180}\right)\centerdot{tan}\left(−{x}\right)\centerdot{sin}\left(\mathrm{90}−{x}\right)\centerdot{cos}\left(\mathrm{360}−{x}\right)}{{sin}\left(\mathrm{180}−{x}\right)}=? \\ $$

Question Number 142255 Answers: 1 Comments: 0

find the value of ∫_0 ^1 (√(x^4 −5x^2 +4)) dx? solution please.

$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}^{\mathrm{4}} −\mathrm{5x}^{\mathrm{2}} +\mathrm{4}}\:\mathrm{dx}? \\ $$$$\mathrm{solution}\:\mathrm{please}. \\ $$

Question Number 142256 Answers: 1 Comments: 0

∫_0 ^∞ ((sinx)/x^(1−a) )dx

$$\int_{\mathrm{0}} ^{\infty} \frac{{sinx}}{{x}^{\mathrm{1}−{a}} }{dx} \\ $$

Pg 765 Pg 766 Pg 767 Pg 768 Pg 769 Pg 770 Pg 771 Pg 772 Pg 773 Pg 774

Contact: info@tinkutara.com