Question and Answers Forum

AllQuestion and Answers: Page 758

Question Number 141931 Answers: 2 Comments: 0

calculate ∫_0 ^∞ e^(−2x) ln(1+e^(3x) )dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2x}} \mathrm{ln}\left(\mathrm{1}+\mathrm{e}^{\mathrm{3x}} \right)\mathrm{dx} \\ $$

Question Number 141930 Answers: 0 Comments: 0

calculate ∫_0 ^∞ e^(−(x^3 +(1/x^3 ))) dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{x}^{\mathrm{3}} \:+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right)} \mathrm{dx} \\ $$

Question Number 141929 Answers: 1 Comments: 0

find ∫_0 ^∞ e^(−(t^2 +(1/t^2 ))) dt

$$\mathrm{find}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\left(\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\right)} \mathrm{dt} \\ $$

Question Number 141924 Answers: 1 Comments: 1

cos(x−180)=?

$${cos}\left({x}−\mathrm{180}\right)=? \\ $$

Question Number 142263 Answers: 0 Comments: 0

(((0 sin(x))),((0 0)) )!+ (((0 sin(2x))),((0 0)) )!+ (((0 sin(3x))),((0 0)) )!+... n^(th) term

$$\begin{pmatrix}{\mathrm{0}\:{sin}\left({x}\right)}\\{\mathrm{0}\:\:\mathrm{0}}\end{pmatrix}!+\begin{pmatrix}{\mathrm{0}\:\:{sin}\left(\mathrm{2}{x}\right)}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}!+\begin{pmatrix}{\mathrm{0}\:\:\:{sin}\left(\mathrm{3}{x}\right)}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}!+...\:{n}^{{th}} \:{term} \\ $$

Question Number 141916 Answers: 1 Comments: 0

prove that:: I:=∫_0 ^( (π/2)) arccosh(sin(x)+cos(x))dx=(π/2)ln(2) ..

$$ \\ $$$$\:\:\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\mathrm{I}:=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {arccosh}\left({sin}\left({x}\right)+{cos}\left({x}\right)\right){dx}=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:.. \\ $$

Question Number 141914 Answers: 3 Comments: 0

prove that:: φ:=∫_0 ^( π) (x/((sin(x))^(1/2) ))dx=(√(π/8)) Γ^( 2) ((1/4))...✓ .........

$$\:\:\:\: \\ $$$$\:\:\:\:\:\:{prove}\:{that}:: \\ $$$$\:\:\:\:\:\phi:=\int_{\mathrm{0}} ^{\:\pi} \frac{{x}}{\left({sin}\left({x}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{dx}=\sqrt{\frac{\pi}{\mathrm{8}}}\:\Gamma^{\:\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)...\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:......... \\ $$

Question Number 141912 Answers: 0 Comments: 0

Q138579

$${Q}\mathrm{138579} \\ $$

Question Number 141911 Answers: 0 Comments: 0

Q137956

$${Q}\mathrm{137956} \\ $$

Question Number 141910 Answers: 0 Comments: 0

Q137026

$${Q}\mathrm{137026} \\ $$

Question Number 141909 Answers: 1 Comments: 1

Question Number 141908 Answers: 0 Comments: 0

Q137984

$${Q}\mathrm{137984} \\ $$$$ \\ $$

Question Number 141907 Answers: 0 Comments: 0

Q140000

$${Q}\mathrm{140000} \\ $$

Question Number 141905 Answers: 0 Comments: 0

Q137503

$${Q}\mathrm{137503} \\ $$

Question Number 141901 Answers: 0 Comments: 1

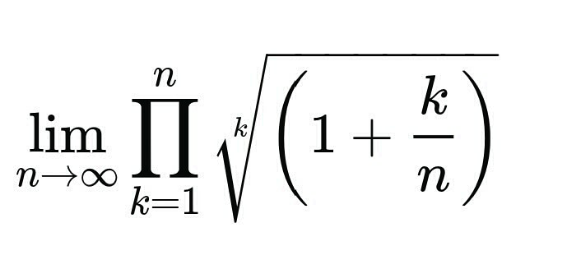
Question Number 141900 Answers: 2 Comments: 0

L = lim_(x→0) ((e^x cos x−x−1)/x^3 ) =?

$$\:\mathcal{L}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{e}^{{x}} \:\mathrm{cos}\:{x}−{x}−\mathrm{1}}{{x}^{\mathrm{3}} }\:=? \\ $$

Question Number 141890 Answers: 0 Comments: 1

Question Number 141885 Answers: 3 Comments: 0

easy question: if lim_(x→0) ((1−cos(1−cos(1−cos(x))))/x^8 ) =2^( a) then a=??

$$\:\:\: \\ $$$$\:\:\:\:\:\:{easy}\:\:{question}: \\ $$$$\:\:\:\:{if}\:\:\:{lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−{cos}\left(\mathrm{1}−{cos}\left(\mathrm{1}−{cos}\left({x}\right)\right)\right)}{{x}^{\mathrm{8}} }\:=\mathrm{2}^{\:{a}} \\ $$$$\:\:\:\:\:\:\:\:{then}\:\:\:{a}=??\:\: \\ $$

Question Number 141884 Answers: 0 Comments: 0

Question Number 141868 Answers: 1 Comments: 1

......Advanced .....Calculus........ ..... ∫_( R) ^ (e^(−x^2 ) /((1+x^2 )^2 )) dx=?

$$\:\:\:\:\:\:\:\:\:\:\:\:......\mathscr{A}{dvanced}\:\:.....\mathscr{C}{alculus}........ \\ $$$$\:\:\:\:\:\:\:\:\:.....\:\:\int_{\:\mathbb{R}} ^{\:} \frac{{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dx}=? \\ $$$$\:\:\:\:\: \\ $$

Question Number 141859 Answers: 2 Comments: 1

∫_0 ^∞ ((4e^(−x^2 ) )/((2x^2 +1)^2 )) dx

$$\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{4}{e}^{−{x}^{\mathrm{2}} } }{\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\: \\ $$

Question Number 141858 Answers: 1 Comments: 1

Question Number 141872 Answers: 1 Comments: 2

Question Number 141849 Answers: 1 Comments: 0

y′′−6y′+9y = 9x^2 e^(3x) cos (3x)

$$\:\:\:\:\:{y}''−\mathrm{6}{y}'+\mathrm{9}{y}\:=\:\mathrm{9}{x}^{\mathrm{2}} \:{e}^{\mathrm{3}{x}} \:\mathrm{cos}\:\left(\mathrm{3}{x}\right)\:\: \\ $$

Question Number 141848 Answers: 4 Comments: 0

I = ∫ (1/( (√(1−x^2 ))−1)) dx

$$\:\mathscr{I}\:=\:\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1}}\:{dx}\: \\ $$

Question Number 141847 Answers: 2 Comments: 0

I = ∫ ((sec x)/(1+csc x)) dx

$$\:\mathcal{I}\:=\:\int\:\frac{\mathrm{sec}\:{x}}{\mathrm{1}+\mathrm{csc}\:{x}}\:{dx}\: \\ $$

Pg 753 Pg 754 Pg 755 Pg 756 Pg 757 Pg 758 Pg 759 Pg 760 Pg 761 Pg 762

Contact: info@tinkutara.com