Question and Answers Forum

AllQuestion and Answers: Page 756

Question Number 142802 Answers: 1 Comments: 1

x=2w(e^(−1) )

$${x}=\mathrm{2}{w}\left({e}^{−\mathrm{1}} \right) \\ $$

Question Number 142794 Answers: 3 Comments: 0

If 2cos (((5π)/4)+3x)cos ((π/4)+3x)=0 and sin (2x−2y)=cos y where (π/4)≤x≤(π/2) and (π/4)≤y≤(π/2) . find the value of { ((sin (2x+y))),((cos (2x+y))),((cos (2x−y))),((sin (2x−y))) :}

$$\mathrm{If}\:\mathrm{2cos}\:\left(\frac{\mathrm{5}\pi}{\mathrm{4}}+\mathrm{3x}\right)\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}+\mathrm{3x}\right)=\mathrm{0}\:\mathrm{and}\: \\ $$$$\mathrm{sin}\:\left(\mathrm{2x}−\mathrm{2y}\right)=\mathrm{cos}\:\mathrm{y}\:\mathrm{where}\:\frac{\pi}{\mathrm{4}}\leqslant\mathrm{x}\leqslant\frac{\pi}{\mathrm{2}}\:\mathrm{and} \\ $$$$\frac{\pi}{\mathrm{4}}\leqslant\mathrm{y}\leqslant\frac{\pi}{\mathrm{2}}\:.\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\begin{cases}{\mathrm{sin}\:\left(\mathrm{2x}+\mathrm{y}\right)}\\{\mathrm{cos}\:\left(\mathrm{2x}+\mathrm{y}\right)}\\{\mathrm{cos}\:\left(\mathrm{2x}−\mathrm{y}\right)}\\{\mathrm{sin}\:\left(\mathrm{2x}−\mathrm{y}\right)}\end{cases} \\ $$

Question Number 142791 Answers: 1 Comments: 0

Evaluate:: ... Ω :=∫_0 ^( 1) ((li_2 ((√x) ))/(1+(√x))) dx=?? ...........

$$\:\:\:{Evaluate}::\:... \\ $$$$\:\:\:\:\:\:\:\Omega\::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{li}_{\mathrm{2}} \left(\sqrt{{x}}\:\right)}{\mathrm{1}+\sqrt{{x}}}\:{dx}=?? \\ $$$$\:\:\:\:........... \\ $$

Question Number 142789 Answers: 2 Comments: 0

∫e^(x^2 /2) dx = ??

$$\int{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:{dx}\:=\:?? \\ $$

Question Number 142788 Answers: 1 Comments: 0

Question Number 142777 Answers: 0 Comments: 2

Question Number 142773 Answers: 2 Comments: 0

.......nice ......integral...... 𝛗:=∫_(0 ) ^( 1) ((li_2 (1−x))/(2−x)) dx=?? .......m.n...

$$\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:.......{nice}\:......{integral}...... \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\phi}:=\int_{\mathrm{0}\:} ^{\:\mathrm{1}} \frac{{li}_{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{\mathrm{2}−{x}}\:{dx}=?? \\ $$$$\:.......{m}.{n}... \\ $$

Question Number 142755 Answers: 1 Comments: 2

log_3 x^3 +log_2 x^2 =((2lg6)/(lg2))+1 find x

$$\mathrm{log}_{\mathrm{3}} \mathrm{x}^{\mathrm{3}} +\mathrm{log}_{\mathrm{2}} \mathrm{x}^{\mathrm{2}} =\frac{\mathrm{2lg6}}{\mathrm{lg2}}+\mathrm{1}\:\:\mathrm{find}\:\:\mathrm{x} \\ $$

Question Number 142748 Answers: 0 Comments: 0

please only number 4

$${please}\:{only}\:{number}\:\mathrm{4} \\ $$

Question Number 142745 Answers: 0 Comments: 7

Question Number 142814 Answers: 0 Comments: 4

Question Number 142815 Answers: 0 Comments: 1

find all roots of m^8 +7m^6 +2m^5 −12=0

$${find}\:{all}\:{roots}\:{of}\: \\ $$$$ \\ $$$${m}^{\mathrm{8}} +\mathrm{7}{m}^{\mathrm{6}} +\mathrm{2}{m}^{\mathrm{5}} −\mathrm{12}=\mathrm{0} \\ $$

Question Number 142740 Answers: 3 Comments: 3

(a/(b+c)) = (b/(a+c)) = (c/(a+b)) ; a∙b∙c = 12 (b+c)∙(a+c)∙(a+b) = ?

$$\frac{{a}}{{b}+{c}}\:=\:\frac{{b}}{{a}+{c}}\:=\:\frac{{c}}{{a}+{b}}\:\:;\:\:{a}\centerdot{b}\centerdot{c}\:=\:\mathrm{12} \\ $$$$\left({b}+{c}\right)\centerdot\left({a}+{c}\right)\centerdot\left({a}+{b}\right)\:=\:? \\ $$

Question Number 142730 Answers: 0 Comments: 1

x^x^(30) =(√)2^(1/2)

$${x}^{{x}^{\mathrm{30}} } =\sqrt{}\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$

Question Number 142729 Answers: 1 Comments: 0

prove:(d/dz)(tan^(−1) z)=(1/(1+z^2 )) in complex number help me sir

$${prove}:\frac{{d}}{{dz}}\left({tan}^{−\mathrm{1}} {z}\right)=\frac{\mathrm{1}}{\mathrm{1}+{z}^{\mathrm{2}} }\:{in}\:{complex}\:{number} \\ $$$${help}\:{me}\:{sir} \\ $$$$ \\ $$

Question Number 142725 Answers: 1 Comments: 7

Question Number 142724 Answers: 2 Comments: 0

∫_0 ^(π/2) ((sin(2t))/(1+xsin(2t)))dt=....

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}\left(\mathrm{2}{t}\right)}{\mathrm{1}+{xsin}\left(\mathrm{2}{t}\right)}{dt}=.... \\ $$

Question Number 142723 Answers: 1 Comments: 0

....... discrete ..... mathematics....... prove that: Σ_(n=1) ^∞ (1/(F_(2n+1) −1))=^? ((5−(√5))/2) F_n :: fibonacci sequence...

$$\:\:\:\:\:\:\:\:.......\:{discrete}\:\:.....\:\:{mathematics}....... \\ $$$$\:\:\:\:{prove}\:{that}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{F}_{\mathrm{2}{n}+\mathrm{1}} −\mathrm{1}}\overset{?} {=}\frac{\mathrm{5}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:{F}_{{n}} \:::\:{fibonacci}\:\:{sequence}... \\ $$

Question Number 142721 Answers: 1 Comments: 0

lim_(x→0) (x/( (√(1−cos x))))=?

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}}{\:\sqrt{\mathrm{1}−\mathrm{cos}\:{x}}}=? \\ $$

Question Number 142719 Answers: 0 Comments: 1

find the particular solution to the differential equation y^((4)) +21y^((2)) −100y=4(8−29t)e^(−2t) . solution please.

$$\mathrm{find}\:\mathrm{the}\:\mathrm{particular}\:\mathrm{solution} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{differential}\:\mathrm{equation} \\ $$$$\mathrm{y}^{\left(\mathrm{4}\right)} +\mathrm{21y}^{\left(\mathrm{2}\right)} −\mathrm{100y}=\mathrm{4}\left(\mathrm{8}−\mathrm{29t}\right)\mathrm{e}^{−\mathrm{2t}} . \\ $$$$\mathrm{solution}\:\mathrm{please}. \\ $$

Question Number 142717 Answers: 2 Comments: 1

Question Number 142765 Answers: 1 Comments: 1

A class has 13 children. To play a game one child is the referee and the other children are divided in three teams with four children in each team. In how many ways can the class play the game?

$${A}\:{class}\:{has}\:\mathrm{13}\:{children}.\:{To}\:{play}\:{a} \\ $$$${game}\:{one}\:{child}\:{is}\:{the}\:{referee}\:{and}\:{the} \\ $$$${other}\:{children}\:{are}\:{divided}\:{in}\:{three}\: \\ $$$${teams}\:{with}\:{four}\:{children}\:{in}\:{each}\:{team}. \\ $$$${In}\:{how}\:{many}\:{ways}\:{can}\:{the}\:{class}\:{play} \\ $$$${the}\:{game}? \\ $$

Question Number 142763 Answers: 2 Comments: 2

Question Number 142712 Answers: 0 Comments: 0

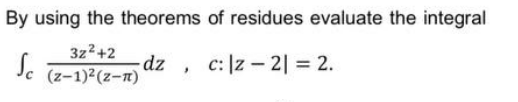
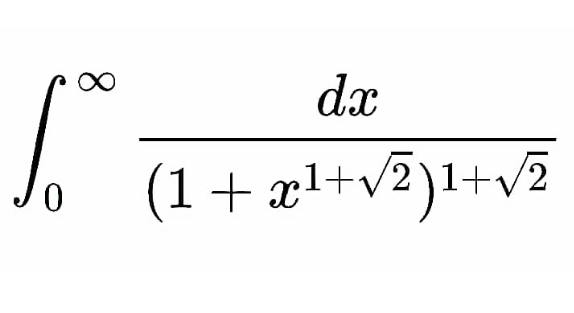
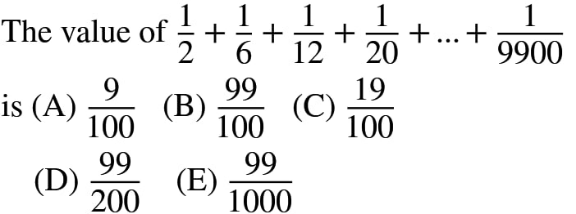
Question Number 142710 Answers: 1 Comments: 0

Let k be non-negative real numbers and n ∈ N^+ ≥1. Prove that (((4−k)/(4+k)))(((12−k)/(12+k)))...[((2n(n+1)−k)/(2n(n+1)+k))] ≤ ((n+k+1)/((n+1)(k+1)))

$$\mathrm{Let}\:{k}\:\mathrm{be}\:\mathrm{non}-\mathrm{negative}\:\mathrm{real}\:\mathrm{numbers}\:\mathrm{and}\:{n}\:\in\:\mathrm{N}^{+} \geqslant\mathrm{1}.\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\frac{\mathrm{4}−{k}}{\mathrm{4}+{k}}\right)\left(\frac{\mathrm{12}−{k}}{\mathrm{12}+{k}}\right)...\left[\frac{\mathrm{2}{n}\left({n}+\mathrm{1}\right)−{k}}{\mathrm{2}{n}\left({n}+\mathrm{1}\right)+{k}}\right]\:\leqslant\:\frac{{n}+{k}+\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({k}+\mathrm{1}\right)} \\ $$$$ \\ $$

Question Number 142708 Answers: 1 Comments: 0

I=∫_0 ^( α) (√(c^2 −sin^2 θ))dθ tan α=(a^2 /b^2 ) , a^2 >b^2 , c^2 >1 Perimeter of ellipse =4∫_0 ^( π/2) (√(a^2 −(a^2 −b^2 )sin^2 θ)) dθ (is that right sir?)

$$\:{I}=\int_{\mathrm{0}} ^{\:\:\alpha} \sqrt{{c}^{\mathrm{2}} −\mathrm{sin}\:^{\mathrm{2}} \theta}{d}\theta \\ $$$$\:\mathrm{tan}\:\alpha=\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }\:\:,\:{a}^{\mathrm{2}} >{b}^{\mathrm{2}} \:\:,\:{c}^{\mathrm{2}} >\mathrm{1} \\ $$$${Perimeter}\:{of}\:{ellipse} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \sqrt{{a}^{\mathrm{2}} −\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)\mathrm{sin}\:^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$\left({is}\:{that}\:{right}\:{sir}?\right) \\ $$

Pg 751 Pg 752 Pg 753 Pg 754 Pg 755 Pg 756 Pg 757 Pg 758 Pg 759 Pg 760

Contact: info@tinkutara.com