Question and Answers Forum

AllQuestion and Answers: Page 755

Question Number 143134 Answers: 1 Comments: 0

Question Number 143131 Answers: 2 Comments: 0

find the partial sums of Σ_(n=1) ^∞ (1/(n^2 (n+1)))

$${find}\:{the}\:{partial}\:{sums}\:{of}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)} \\ $$

Question Number 143130 Answers: 1 Comments: 1

Question Number 143127 Answers: 2 Comments: 0

Question Number 143122 Answers: 0 Comments: 0

Let a,b ∈[0,1] and a+b ≤ 1. Prove that (1/(1+a))+(1/(1+b))+(1/2) ≤ (2/(a+b))

$$\mathrm{Let}\:{a},{b}\:\in\left[\mathrm{0},\mathrm{1}\right]\:\mathrm{and}\:{a}+{b}\:\leqslant\:\mathrm{1}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}+{a}}+\frac{\mathrm{1}}{\mathrm{1}+{b}}+\frac{\mathrm{1}}{\mathrm{2}}\:\leqslant\:\frac{\mathrm{2}}{{a}+{b}}\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$

Question Number 143114 Answers: 1 Comments: 0

solve: lim_(z→i) ((3z^4 −2z^3 +8z^2 −2z+5)/(z−i))=?

$${solve}: \\ $$$$\underset{{z}\rightarrow{i}} {\mathrm{lim}}\frac{\mathrm{3}{z}^{\mathrm{4}} −\mathrm{2}{z}^{\mathrm{3}} +\mathrm{8}{z}^{\mathrm{2}} −\mathrm{2}{z}+\mathrm{5}}{{z}−{i}}=? \\ $$

Question Number 143113 Answers: 0 Comments: 1

x^3 =(1/(3!))∫_0 ^x f(x−t)f(t)dt f(x)=?

$$\mathrm{x}^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{3}!}\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{f}\left(\mathrm{x}−\mathrm{t}\right)\mathrm{f}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=? \\ $$

Question Number 143109 Answers: 3 Comments: 1

Question Number 143105 Answers: 0 Comments: 1

((cos(3x))/(sin(2x))) = 0

$$\frac{{cos}\left(\mathrm{3}{x}\right)}{{sin}\left(\mathrm{2}{x}\right)}\:=\:\mathrm{0} \\ $$

Question Number 143102 Answers: 1 Comments: 0

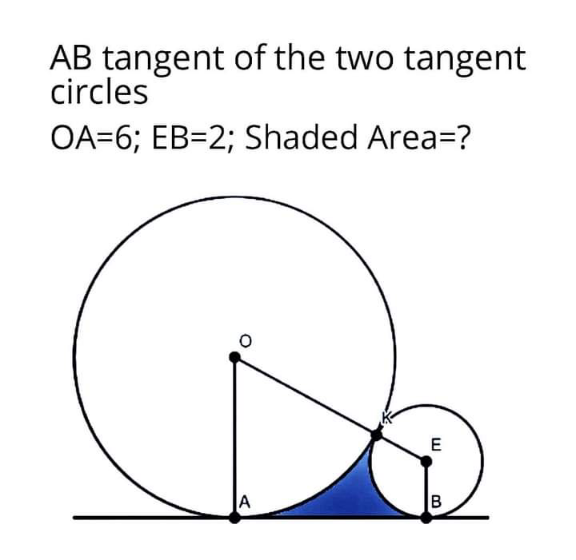
Question Number 143101 Answers: 0 Comments: 0

Find x: x^(x+1) =(x+1)^x

$$\mathrm{Find}\:\mathrm{x}:\:\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{x}+\mathrm{1}} =\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{x}} \\ $$

Question Number 143100 Answers: 5 Comments: 0

∫(√(e^x +1 ))=.....???

$$\int\sqrt{{e}^{{x}} +\mathrm{1}\:}=.....??? \\ $$

Question Number 143098 Answers: 1 Comments: 0

.....Prove.... Σ_(n=1) ^∞ ((1/(sinh(πn))))^2 =(1/6) −(1/(2π)) ... ......

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....{Prove}....\: \\ $$$$\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{s}{inh}\left(\pi{n}\right)}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{6}}\:−\frac{\mathrm{1}}{\mathrm{2}\pi}\:\:\:... \\ $$$$\:\:\:\:\:\:\:...... \\ $$

Question Number 143097 Answers: 1 Comments: 0

If z=cos θ+isin θ, prove that ((1−z^2 )/(1+z^2 ))=−itan θ

$$\mathrm{If}\:{z}=\mathrm{cos}\:\theta+{i}\mathrm{sin}\:\theta,\: \\ $$$$\mathrm{prove}\:\mathrm{that}\:\frac{\mathrm{1}−{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} }=−{i}\mathrm{tan}\:\theta \\ $$

Question Number 143094 Answers: 1 Comments: 0

Question Number 143090 Answers: 0 Comments: 0

Question Number 143087 Answers: 2 Comments: 0

Question Number 143086 Answers: 2 Comments: 0

Evaluate :: Ω:=∫_0 ^( (π/4)) ((ln(tan(x)).sin^π^e (2x))/((sin^π^e (x)+cos^π^e (x))^2 ))dx

$$ \\ $$$$\:\:{Evaluate}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Omega:=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{4}}} \frac{{ln}\left({tan}\left({x}\right)\right).{sin}^{\pi^{{e}} } \left(\mathrm{2}{x}\right)}{\left({sin}^{\pi^{{e}} } \left({x}\right)+{cos}^{\pi^{{e}} } \left({x}\right)\right)^{\mathrm{2}} }{dx} \\ $$$$ \\ $$

Question Number 143085 Answers: 0 Comments: 0

φ(n^4 +1)=8n φ:Euler totient function Solve for n∈N

$$\phi\left({n}^{\mathrm{4}} +\mathrm{1}\right)=\mathrm{8}{n}\:\:\:\:\:\:\phi:{Euler}\:{totient}\:{function} \\ $$$${Solve}\:{for}\:{n}\in\mathbb{N} \\ $$

Question Number 143083 Answers: 1 Comments: 0

calculate Ψ(a,b)=∫_0 ^∞ (e^(−ax^2 ) /((x^2 +b^2 )^2 ))dx with a>0 and b>0

$${calculate}\:\Psi\left({a},{b}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{ax}^{\mathrm{2}} } }{\left({x}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx} \\ $$$${with}\:{a}>\mathrm{0}\:{and}\:{b}>\mathrm{0} \\ $$

Question Number 143082 Answers: 2 Comments: 0

calculate f(a,b)=∫_0 ^∞ (e^(−ax^2 ) /(x^2 +b^2 ))dx with a>0 and b>0

$${calculate}\:{f}\left({a},{b}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{ax}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \:+{b}^{\mathrm{2}} }{dx} \\ $$$${with}\:{a}>\mathrm{0}\:{and}\:{b}>\mathrm{0} \\ $$

Question Number 143081 Answers: 2 Comments: 0

calculate ∫_0 ^∞ xe^(−x^2 ) arctanx dx

$${calculate}\:\int_{\mathrm{0}} ^{\infty} {xe}^{−{x}^{\mathrm{2}} } {arctanx}\:{dx} \\ $$

Question Number 143080 Answers: 2 Comments: 0

calculate ∫_0 ^∞ ((arctan(x^2 ))/(1+x^2 ))dx

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{arctan}\left({x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$

Question Number 143077 Answers: 1 Comments: 0

sin^5 x + cos^5 x = 2 − sin^4 x

$${sin}^{\mathrm{5}} {x}\:+\:{cos}^{\mathrm{5}} {x}\:=\:\mathrm{2}\:−\:{sin}^{\mathrm{4}} {x} \\ $$

Question Number 143072 Answers: 1 Comments: 0

Question Number 143071 Answers: 2 Comments: 0

∫_0 ^(π/4) ((8dx)/(tgx+1))

$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{8}{dx}}{{tgx}+\mathrm{1}} \\ $$

Pg 750 Pg 751 Pg 752 Pg 753 Pg 754 Pg 755 Pg 756 Pg 757 Pg 758 Pg 759

Contact: info@tinkutara.com