Question and Answers Forum

AllQuestion and Answers: Page 754

Question Number 143519 Answers: 3 Comments: 0

The first two terms of the {a_n } series are defind as a_n =a_(n−1) +a_(n−2) for the general term a_1 =5, a_2 =8 and n≥3 . since the L=lim_(n→∞) (a_(n+1) /a_n ) what is the value of L

$$ \\ $$$${The}\:{first}\:{two}\:{terms}\:{of}\:{the}\:\left\{{a}_{{n}} \right\}\:{series}\:\:\:{are}\:{defind}\:{as}\:{a}_{{n}} ={a}_{{n}−\mathrm{1}} +{a}_{{n}−\mathrm{2}} \:\:{for}\:{the}\:{general}\:{term} \\ $$$$\:{a}_{\mathrm{1}} =\mathrm{5},\:{a}_{\mathrm{2}} =\mathrm{8}\:{and}\:{n}\geqslant\mathrm{3}\:. \\ $$$${since}\:{the}\:{L}={li}\underset{{n}\rightarrow\infty} {{m}}\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }\:\:{what}\:{is}\:{the}\:{value}\:{of}\:{L} \\ $$$$ \\ $$

Question Number 143516 Answers: 2 Comments: 1

Question Number 143508 Answers: 3 Comments: 0

..........Calculus........ i: 𝛗_1 :=∫_0 ^( 1) ((ln^2 (1−x).ln(x))/x)dx ii: 𝛗_2 := ∫_0 ^( 1) ((ln^2 (x).ln(1−x))/x) dx iii : 𝛗_3 :=∫_0 ^( 1) ((ln^2 (x).ln(1+x))/x)dx

$$ \\ $$$$\:\:\:\:\:\:\:\:..........{Calculus}........ \\ $$$$\:\:\:\:{i}:\:\:\:\boldsymbol{\phi}_{\mathrm{1}} :=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right).{ln}\left({x}\right)}{{x}}{dx} \\ $$$$\:\:\:{ii}:\:\:\:\boldsymbol{\phi}_{\mathrm{2}} :=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right).{ln}\left(\mathrm{1}−{x}\right)}{{x}}\:{dx} \\ $$$$\:\:{iii}\::\:\boldsymbol{\phi}_{\mathrm{3}} \::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right).{ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx} \\ $$

Question Number 143507 Answers: 1 Comments: 0

10(√(20))+13(√(45))

$$\mathrm{10}\sqrt{\mathrm{20}}+\mathrm{13}\sqrt{\mathrm{45}} \\ $$

Question Number 143506 Answers: 1 Comments: 0

∫_1 ^∞ (1/(e^(−x) +e^x )) dx=?

$$\underset{\mathrm{1}} {\overset{\infty} {\int}}\frac{\mathrm{1}}{{e}^{−{x}} +{e}^{{x}} }\:{dx}=? \\ $$$$ \\ $$

Question Number 143505 Answers: 1 Comments: 1

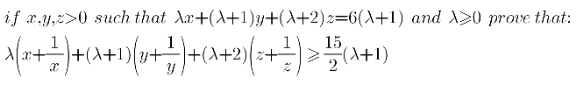
Question Number 143501 Answers: 0 Comments: 0

Question Number 143502 Answers: 0 Comments: 0

Question Number 143499 Answers: 1 Comments: 1

Question Number 143514 Answers: 0 Comments: 1

Question Number 143495 Answers: 1 Comments: 0

On definit la fonction L(f(t))(p)=∫_0 ^(+∞) f(t)e^(−pt) dt Calculer L(((t^n /(n!))))(p)

$${On}\:{definit}\:{la}\:{fonction}\: \\ $$$$\mathscr{L}\left({f}\left({t}\right)\right)\left({p}\right)=\int_{\mathrm{0}} ^{+\infty} {f}\left({t}\right){e}^{−{pt}} {dt} \\ $$$${Calculer}\:\mathscr{L}\left(\left(\frac{{t}^{{n}} }{{n}!}\right)\right)\left({p}\right) \\ $$

Question Number 143493 Answers: 0 Comments: 1

Question Number 143491 Answers: 0 Comments: 1

Find lim_(n→+∝) (u_n ),If { ((u_0 =1,n=1,2,3,.....)),((u_n = ((2018)/(2019))u_(n−1) + (1/((u_(n−1) )^(2018) )))) :}

$$\mathrm{Find}\:\underset{\mathrm{n}\rightarrow+\propto} {\mathrm{lim}}\left(\mathrm{u}_{\mathrm{n}} \right),\mathrm{If}\:\begin{cases}{\mathrm{u}_{\mathrm{0}} =\mathrm{1},\mathrm{n}=\mathrm{1},\mathrm{2},\mathrm{3},.....}\\{\mathrm{u}_{\mathrm{n}} =\:\frac{\mathrm{2018}}{\mathrm{2019}}\mathrm{u}_{\mathrm{n}−\mathrm{1}} +\:\frac{\mathrm{1}}{\left(\mathrm{u}_{\mathrm{n}−\mathrm{1}} \right)^{\mathrm{2018}} }}\end{cases} \\ $$

Question Number 143488 Answers: 1 Comments: 0

let f(x)=(1/(2+sinx)) developp f at fourier serie

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}+\mathrm{sinx}} \\ $$$$\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$

Question Number 143487 Answers: 0 Comments: 0

find ∫_0 ^1 ((log(1+t^2 ))/(1+t))dt

$$\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$

Question Number 143481 Answers: 1 Comments: 3

1−Montrer par recurrence que la transformee deLaplace suivante L(f^n (t))(p)=p^n L(f(t)(p)−p^(n−1) f(0^+ )−p^(n−2) f ′(0^+ )−.......−f^((n−1)) (0^+ ) 2−Calaculer partir de L(sint)(p) la transforme L(((sint)/t))(p)

$$\mathrm{1}−{Montrer}\:{par}\:{recurrence}\:{que}\:{la}\:{transformee}\:{deLaplace}\:{suivante} \\ $$$$\mathscr{L}\left({f}^{{n}} \left({t}\right)\right)\left({p}\right)={p}^{{n}} \mathscr{L}\left({f}\left({t}\right)\left({p}\right)−{p}^{{n}−\mathrm{1}} {f}\left(\mathrm{0}^{+} \right)−{p}^{{n}−\mathrm{2}} {f}\:'\left(\mathrm{0}^{+} \right)−.......−{f}^{\left({n}−\mathrm{1}\right)} \left(\mathrm{0}^{+} \right)\right. \\ $$$$ \\ $$$$\mathrm{2}−{Calaculer}\:{partir}\:{de}\:\mathscr{L}\left({sint}\right)\left({p}\right)\:{la}\:{transforme}\:\mathscr{L}\left(\frac{{sint}}{{t}}\right)\left({p}\right) \\ $$

Question Number 143477 Answers: 0 Comments: 0

∫_0 ^1 e^(2arctg(t^2 )) dt

$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{\mathrm{2}{arctg}\left({t}^{\mathrm{2}} \right)} {dt} \\ $$

Question Number 143475 Answers: 1 Comments: 1

evaluate; ((((√7))^(log64) −(3)^(log_(24) 8) )/((log _2 8−log _(1/4) 64)((1/(log _4 ((1/(64))))))))

$$\:{evaluate}; \\ $$$$\frac{\left(\sqrt{\mathrm{7}}\right)^{\mathrm{log64}} −\left(\mathrm{3}\right)^{\mathrm{log}_{\mathrm{24}} \mathrm{8}} }{\left(\mathrm{log}\:_{\mathrm{2}} \mathrm{8}−\mathrm{log}\:_{\frac{\mathrm{1}}{\mathrm{4}}} \mathrm{64}\right)\left(\frac{\mathrm{1}}{\mathrm{log}\:_{\mathrm{4}} \left(\frac{\mathrm{1}}{\mathrm{64}}\right)}\right)} \\ $$

Question Number 143463 Answers: 0 Comments: 0

Π_(k=1) ^n tan(((kπ)/(2n+1)))=(√(2n+1))

$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{tan}\left(\frac{{k}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)=\sqrt{\mathrm{2}{n}+\mathrm{1}} \\ $$

Question Number 143462 Answers: 3 Comments: 0

lim_(x→1) ((x−1)/(ln((x/(2−x))))) = ???

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\:\:\frac{{x}−\mathrm{1}}{{ln}\left(\frac{{x}}{\mathrm{2}−{x}}\right)}\:=\:??? \\ $$

Question Number 143461 Answers: 3 Comments: 0

Prove that : ∀n∈N^∗ a. Σ_(k=1) ^n C_n ^k (((−1)^k )/k) = Σ_(k=1) ^n (1/k) b. Σ_(k=1) ^n C_n ^k (((−1)^k )/(2k+1)) = (4^n /((2n+1)C_(2n) ^n ))

$$\mathrm{Prove}\:\mathrm{that}\::\:\forall\mathrm{n}\in\mathbb{N}^{\ast} \\ $$$$\mathrm{a}.\:\:\:\:\:\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}{C}_{\mathrm{n}} ^{\mathrm{k}} \frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{k}}\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{k}} \\ $$$$\mathrm{b}.\:\:\:\:\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}{C}_{\mathrm{n}} ^{\mathrm{k}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{2k}+\mathrm{1}}\:=\:\frac{\mathrm{4}^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right){C}_{\mathrm{2n}} ^{\mathrm{n}} } \\ $$

Question Number 143474 Answers: 0 Comments: 0

for all positive integral., u_(n+1) =u_n (u_(n−1) ^2 −2)−u_n u_n =2 and u_1 =2(1/2) prove that : 3log_2 [u_n ]=2^n −1(−1)^n where [x] is the integral part of x

$${for}\:{all}\:{positive}\:{integral}., \\ $$$$\:\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\mathrm{u}_{\mathrm{n}} \left(\mathrm{u}_{\mathrm{n}−\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}\right)−\mathrm{u}_{\mathrm{n}} \\ $$$$\:\mathrm{u}_{\mathrm{n}} =\mathrm{2}\:{and}\:\mathrm{u}_{\mathrm{1}} =\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${prove}\:{that}\::\:\mathrm{3log}_{\mathrm{2}} \left[\mathrm{u}_{\mathrm{n}} \right]=\mathrm{2}^{\mathrm{n}} −\mathrm{1}\left(−\mathrm{1}\right)^{\mathrm{n}} \\ $$$${where}\:\left[\mathrm{x}\right]\:{is}\:{the}\:{integral}\:{part}\:{of}\:\:\mathrm{x} \\ $$

Question Number 143453 Answers: 1 Comments: 0

Question Number 143454 Answers: 1 Comments: 0

........nice .......integral....... T :=∫_0 ^( ∞) ((arctan(x))/x^( ln(x) +1) )dx=^? ((π(√π))/4)

$$ \\ $$$$\:\:\:........{nice}\:.......{integral}....... \\ $$$$\:\:\mathscr{T}\:\::=\int_{\mathrm{0}} ^{\:\infty} \frac{{arctan}\left({x}\right)}{{x}^{\:{ln}\left({x}\right)\:+\mathrm{1}} }{dx}\overset{?} {=}\frac{\pi\sqrt{\pi}}{\mathrm{4}} \\ $$$$ \\ $$

Question Number 143450 Answers: 2 Comments: 0

when x+y=((2π)/3); x≥0 ;y≥0 the maximum and the minimum of sin x+sin y is ___

$${when}\:{x}+{y}=\frac{\mathrm{2}\pi}{\mathrm{3}};\:{x}\geqslant\mathrm{0}\:;{y}\geqslant\mathrm{0} \\ $$$${the}\:{maximum}\:{and}\:{the}\:{minimum} \\ $$$${of}\:\mathrm{sin}\:{x}+\mathrm{sin}\:{y}\:{is}\:\_\_\_\: \\ $$

Question Number 145524 Answers: 1 Comments: 0

What is the argument of the complex numbers below (i) z = 1+e^((π/6)i) (ii) z = 1 −e^((π/6)i)

$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{argument}\:\mathrm{of}\:\mathrm{the}\:\mathrm{complex}\:\mathrm{numbers}\:\mathrm{below} \\ $$$$\left(\mathrm{i}\right)\:{z}\:=\:\mathrm{1}+{e}^{\frac{\pi}{\mathrm{6}}{i}} \\ $$$$\left(\mathrm{ii}\right)\:{z}\:=\:\mathrm{1}\:−{e}^{\frac{\pi}{\mathrm{6}}{i}} \\ $$

Pg 749 Pg 750 Pg 751 Pg 752 Pg 753 Pg 754 Pg 755 Pg 756 Pg 757 Pg 758

Contact: info@tinkutara.com