Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 753

Question Number 142502 Answers: 0 Comments: 0

(dy/dx) y= 3a^x −cot 2x

$$\frac{{dy}}{{dx}}\: \\ $$$${y}=\:\mathrm{3}{a}^{{x}} −\mathrm{cot}\:\mathrm{2}{x} \\ $$

Question Number 142499 Answers: 2 Comments: 1

Question Number 142492 Answers: 1 Comments: 0

Prove that Σ_(n = 0) ^∞ (n/(3n^2 + 2)) diverges.

$$\mathrm{Prove}\:\mathrm{that}\:\underset{{n}\:=\:\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}}{\mathrm{3}{n}^{\mathrm{2}} \:+\:\mathrm{2}}\:\mathrm{diverges}. \\ $$

Question Number 142489 Answers: 0 Comments: 3

In a certain urn there are 3 blue, 2red and 5 yellow marbles. Calculate probability that atmost 2 marbles will be red if 3 marbles are drawn without replacement

$$\mathrm{In}\:\:\mathrm{a}\:\mathrm{certain}\:\mathrm{urn}\:\mathrm{there}\:\mathrm{are}\:\mathrm{3}\:\mathrm{blue}, \\ $$$$\mathrm{2red}\:\mathrm{and}\:\mathrm{5}\:\mathrm{yellow}\:\mathrm{marbles}. \\ $$$$\mathrm{Calculate}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{atmost} \\ $$$$\mathrm{2}\:\mathrm{marbles}\:\mathrm{will}\:\mathrm{be}\:\mathrm{red}\:\mathrm{if}\:\mathrm{3}\:\mathrm{marbles} \\ $$$$\:\mathrm{are}\:\mathrm{drawn}\:\mathrm{without}\:\mathrm{replacement} \\ $$

Question Number 142488 Answers: 2 Comments: 0

∫_0 ^1 (t^(k−1) /(1+t^2 ))dt

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{{k}−\mathrm{1}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$

Question Number 142477 Answers: 0 Comments: 0

Question Number 142475 Answers: 2 Comments: 0

Question Number 142469 Answers: 1 Comments: 0

...... Calculus ..... Evaluate: ∫_0 ^( 1) (((log((1/x)))/(1−x)))^3 dx=??

$$\:\:\:\:\:\:\:\:\:\:\:\:......\:\:{Calculus}\:..... \\ $$$$\:\:\:\:{Evaluate}:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{{log}\left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{1}−{x}}\right)^{\mathrm{3}} {dx}=?? \\ $$

Question Number 142467 Answers: 0 Comments: 2

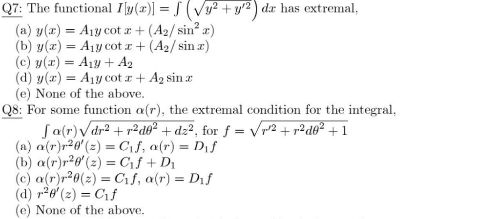
Question Number 142459 Answers: 2 Comments: 0

−−−−−−−−−−− lim_(x→(π/2)) ((x/(cot x))−(π/(2cos x)))=? ___________________

$$\:\:\:\:\:\:−−−−−−−−−−− \\ $$$$\:\:\:\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\:\left(\frac{{x}}{\mathrm{cot}\:{x}}−\frac{\pi}{\mathrm{2cos}\:{x}}\right)=? \\ $$$$\:\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$

Question Number 142457 Answers: 1 Comments: 0

I=∫(dx/( (√(a^2 −(x+(1/x))))))

$$\:{I}=\int\frac{{dx}}{\:\sqrt{{a}^{\mathrm{2}} −\left({x}+\frac{\mathrm{1}}{{x}}\right)}} \\ $$

Question Number 142464 Answers: 2 Comments: 0

lim_(n→∞) [(((2n)!)/(n!n^n ))]^(1/n) =?

$$\underset{\boldsymbol{{n}}\rightarrow\infty} {\boldsymbol{{lim}}}\:\left[\frac{\left(\mathrm{2}\boldsymbol{{n}}\right)!}{\boldsymbol{{n}}!\boldsymbol{{n}}^{\boldsymbol{{n}}} }\right]^{\frac{\mathrm{1}}{\boldsymbol{{n}}}} =? \\ $$

Question Number 142462 Answers: 2 Comments: 0

Question Number 142461 Answers: 2 Comments: 1

Question Number 142447 Answers: 2 Comments: 1

Question Number 142438 Answers: 1 Comments: 0

∫_0 ^1 ((1−x)/(lnx))dx how many tricks solve this

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}}{{lnx}}{dx} \\ $$$${how}\:\:{many}\:{tricks}\:{solve}\:{this} \\ $$

Question Number 142437 Answers: 1 Comments: 0

Question Number 142435 Answers: 0 Comments: 1

Question Number 142430 Answers: 2 Comments: 0

calculate ∫_0 ^∞ ((log^2 x)/(1+x^2 ))dx

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{log}^{\mathrm{2}} {x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$

Question Number 142429 Answers: 1 Comments: 0

calculate U_n =∫_0 ^∞ ((log^n x)/(1+x^n ))dx find nature of the serie ΣU_n

$${calculate}\:{U}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\frac{{log}^{{n}} {x}}{\mathrm{1}+{x}^{{n}} }{dx} \\ $$$${find}\:{nature}\:{of}\:{the}\:{serie}\:\Sigma{U}_{{n}} \\ $$

Question Number 142426 Answers: 1 Comments: 0

find the value of ∫_0 ^∞ ((xlogx)/((1+x^3 )^2 ))dx

$${find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{xlogx}}{\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\mathrm{2}} }{dx} \\ $$

Question Number 142425 Answers: 1 Comments: 0

calculate ∫_0 ^∞ ((log^3 x)/(1+x^3 ))dx

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{log}^{\mathrm{3}} {x}}{\mathrm{1}+{x}^{\mathrm{3}} }{dx} \\ $$

Question Number 142424 Answers: 0 Comments: 0

2)calculate Σ_(k=1) ^(n−1) sin(((kπ)/n)) (n>2) 1) use Rieman sum to prove that ∫_0 ^π log(sinx)dx=−πlog2

$$\left.\mathrm{2}\right){calculate}\:\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} \:{sin}\left(\frac{{k}\pi}{{n}}\right)\:\:\:\left({n}>\mathrm{2}\right) \\ $$$$\left.\mathrm{1}\right)\:{use}\:{Rieman}\:{sum}\:{to}\:{prove} \\ $$$${that}\:\int_{\mathrm{0}} ^{\pi} {log}\left({sinx}\right){dx}=−\pi{log}\mathrm{2} \\ $$

Question Number 142423 Answers: 0 Comments: 0

study the convergence of ∫_0 ^∞ ((log^2 x)/(1+x^2 ))dx

$${study}\:{the}\:{convergence}\:{of} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\frac{{log}^{\mathrm{2}} {x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$

Question Number 142420 Answers: 0 Comments: 0

Question Number 142415 Answers: 1 Comments: 0

(x/(x+4))=((5⌊x⌋−7)/(7⌊x⌋−5)) x=?

$$\frac{{x}}{{x}+\mathrm{4}}=\frac{\mathrm{5}\lfloor{x}\rfloor−\mathrm{7}}{\mathrm{7}\lfloor{x}\rfloor−\mathrm{5}} \\ $$$${x}=? \\ $$

Pg 748 Pg 749 Pg 750 Pg 751 Pg 752 Pg 753 Pg 754 Pg 755 Pg 756 Pg 757

Contact: info@tinkutara.com