Question and Answers Forum

if (a−b)sin(θ+φ)=(a+b)sin(θ−φ) and a tan(θ/2) − b tan(φ/2) = c then prove that the following i) sinφ = ((2bc)/(a^2 −b^2 −c^2 )) ii) sinθ = ((2ac)/(a^2 −b^2 +c^2 ))

$$\mathrm{if}\:\left(\mathrm{a}−\mathrm{b}\right)\mathrm{sin}\left(\theta+\phi\right)=\left(\mathrm{a}+\mathrm{b}\right)\mathrm{sin}\left(\theta−\phi\right)\: \\ $$$$\mathrm{and}\:\mathrm{a}\:\mathrm{tan}\frac{\theta}{\mathrm{2}}\:−\:\mathrm{b}\:\mathrm{tan}\frac{\phi}{\mathrm{2}}\:=\:\mathrm{c}\:\mathrm{then} \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{following} \\ $$$$\left.\mathrm{i}\right)\:\mathrm{sin}\phi\:=\:\frac{\mathrm{2bc}}{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} }\: \\ $$$$\left.\mathrm{ii}\right)\:\mathrm{sin}\theta\:=\:\frac{\mathrm{2ac}}{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} }\: \\ $$

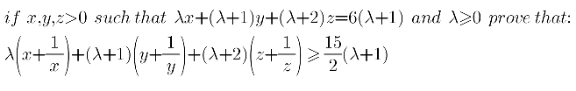
Question Number 144301 Answers: 1 Comments: 0

Question Number 144300 Answers: 1 Comments: 0

Question Number 144293 Answers: 1 Comments: 0

Question Number 144291 Answers: 1 Comments: 0

Question Number 144282 Answers: 1 Comments: 0

I=∫_(π/6) ^(π/3) ((sin^(2021) x)/(sin^(2021) x+cos^(2021) x))dx=?

$$\mathrm{I}=\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} \frac{\mathrm{sin}^{\mathrm{2021}} \mathrm{x}}{\mathrm{sin}^{\mathrm{2021}} \mathrm{x}+\mathrm{cos}^{\mathrm{2021}} \mathrm{x}}\mathrm{dx}=? \\ $$

Question Number 144273 Answers: 1 Comments: 0

Question Number 144272 Answers: 1 Comments: 0

S_n =Σ_(n=1) ^n (1/2^k )tanh((1/2^k ))=?

$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\mathrm{tanh}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\right)=? \\ $$

Question Number 144271 Answers: 3 Comments: 1

a,b,c are in G.P. If a^x =b^y =c^z prove that (1/x),(1/z) are in A.P.

$${a},{b},{c}\:{are}\:{in}\:{G}.{P}.\:{If}\:{a}^{{x}} ={b}^{{y}} ={c}^{{z}} \\ $$$${prove}\:{that}\:\frac{\mathrm{1}}{{x}},\frac{\mathrm{1}}{{z}}\:{are}\:{in}\:{A}.{P}. \\ $$

Question Number 144270 Answers: 1 Comments: 0

Question Number 144269 Answers: 1 Comments: 0

∫_0 ^( ∞) ⌊(y^3 /(e^y −1))⌋dy

$$\int_{\mathrm{0}} ^{\:\infty} \lfloor\frac{{y}^{\mathrm{3}} }{{e}^{{y}} −\mathrm{1}}\rfloor{dy} \\ $$

Question Number 144268 Answers: 2 Comments: 0

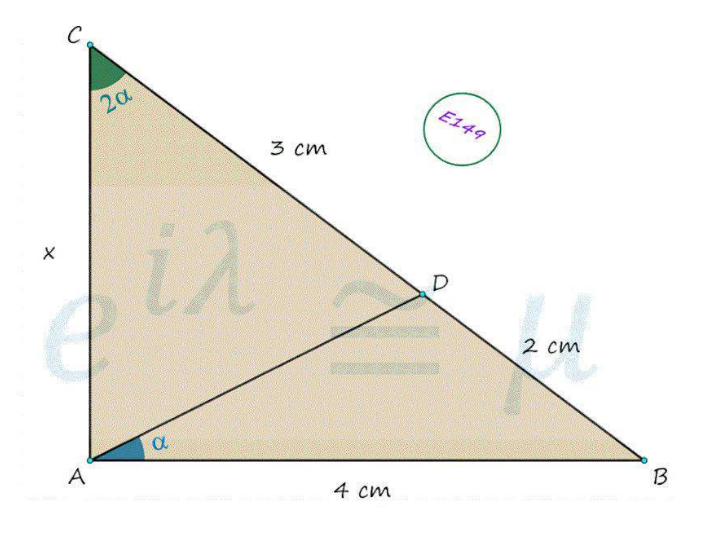
Question Number 144264 Answers: 0 Comments: 0

Let a,b > 0 and 2a+b = 3. Prove the followings: (1) (2/n)a(b+4)+3b^(1/n) ≤ ((10+3n)/n), ∀n∈N^+ ≥1. (2) 2na(b+4)+3b^n ≥ 10n+3, ∀n∈N^+ ≥2.

$$\mathrm{Let}\:{a},{b}\:>\:\mathrm{0}\:\mathrm{and}\:\mathrm{2}{a}+{b}\:=\:\mathrm{3}.\:\mathrm{Prove}\:\mathrm{the}\:\mathrm{followings}:\:\:\:\:\:\:\:\:\:\: \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{{n}}{a}\left({b}+\mathrm{4}\right)+\mathrm{3}{b}^{\frac{\mathrm{1}}{{n}}} \:\leqslant\:\frac{\mathrm{10}+\mathrm{3}{n}}{{n}},\:\forall{n}\in\mathbb{N}^{+} \geqslant\mathrm{1}. \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}{na}\left({b}+\mathrm{4}\right)+\mathrm{3}{b}^{{n}} \:\geqslant\:\mathrm{10}{n}+\mathrm{3},\:\forall{n}\in\mathbb{N}^{+} \geqslant\mathrm{2}. \\ $$$$ \\ $$

Question Number 144261 Answers: 1 Comments: 1

Find the value of lim_(n→∞) Σ_(k=n) ^(2n) (((−1)^k )/k).

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{k}={n}} {\overset{\mathrm{2}{n}} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}. \\ $$

Question Number 144260 Answers: 2 Comments: 0

Find the sum of all the real number x that satisfy (2x^2 +5x+1)^(2x−3) =1

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{all}\:\mathrm{the}\:\mathrm{real}\:\mathrm{number} \\ $$$${x}\:\mathrm{that}\:\mathrm{satisfy}\:\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{5}{x}+\mathrm{1}\right)^{\mathrm{2}{x}−\mathrm{3}} =\mathrm{1} \\ $$

Pg 745 Pg 746 Pg 747 Pg 748 Pg 749 Pg 750 Pg 751 Pg 752 Pg 753 Pg 754

Contact: info@tinkutara.com