Question and Answers Forum

AllQuestion and Answers: Page 749

Question Number 143701 Answers: 1 Comments: 1

Question Number 143698 Answers: 0 Comments: 5

My first Contribution to this forum. One year later Q 98831

$$\:{My}\:{first}\:{Contribution}\:{to}\:{this}\:{forum}.\: \\ $$$${One}\:{year}\:{later}\: \\ $$$${Q}\:\mathrm{98831} \\ $$

Question Number 143688 Answers: 0 Comments: 2

Question Number 143684 Answers: 1 Comments: 0

x^3 +x−1=^3 (√(2x^3 +11))+(√(5x^2 +16)) Find x∈R

$$\mathrm{x}^{\mathrm{3}} +\mathrm{x}−\mathrm{1}=^{\mathrm{3}} \sqrt{\mathrm{2x}^{\mathrm{3}} +\mathrm{11}}+\sqrt{\mathrm{5x}^{\mathrm{2}} +\mathrm{16}} \\ $$$$\mathrm{Find}\:\mathrm{x}\in\mathbb{R} \\ $$

Question Number 143680 Answers: 1 Comments: 1

tan 76=4 sin^2 14=?

$$\mathrm{tan}\:\mathrm{76}=\mathrm{4} \\ $$$$\mathrm{sin}\:^{\mathrm{2}} \mathrm{14}=? \\ $$

Question Number 143677 Answers: 3 Comments: 0

Question Number 143671 Answers: 0 Comments: 2

Question Number 143666 Answers: 2 Comments: 1

Question Number 143653 Answers: 1 Comments: 0

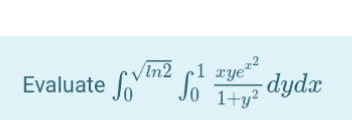
Question Number 143650 Answers: 3 Comments: 0

If the function f and g are defined on the set of real numbers,are such that gof(x)=((2x−5)/(3x+7)) and g(x)=((3x+2)/(x−5)). find an expression for f(x)

$${If}\:\:{the}\:{function}\:{f}\:{and}\:{g}\:{are}\:{defined} \\ $$$${on}\:{the}\:{set}\:{of}\:{real}\:{numbers},{are}\:{such} \\ $$$${that}\:\boldsymbol{{gof}}\left(\boldsymbol{{x}}\right)=\frac{\mathrm{2}\boldsymbol{{x}}−\mathrm{5}}{\mathrm{3}\boldsymbol{{x}}+\mathrm{7}}\:\:\:{and}\: \\ $$$$\boldsymbol{{g}}\left(\boldsymbol{{x}}\right)=\frac{\mathrm{3}\boldsymbol{{x}}+\mathrm{2}}{\boldsymbol{{x}}−\mathrm{5}}. \\ $$$$\boldsymbol{\mathrm{find}}\:\:\boldsymbol{\mathrm{an}}\:\boldsymbol{\mathrm{expression}}\:\boldsymbol{\mathrm{for}}\:\:\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right) \\ $$

Question Number 143889 Answers: 2 Comments: 0

A Challanging Integral: Φ = ∫_0 ^( 1) ((log(x).log(1+x))/(1−x))dx

$$ \\ $$$$\:\:\:\:\:\:{A}\:\:{Challanging}\:\:{Integral}: \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\Phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{log}\left({x}\right).{log}\left(\mathrm{1}+{x}\right)}{\mathrm{1}−{x}}{dx} \\ $$$$ \\ $$$$ \\ $$

Question Number 143641 Answers: 1 Comments: 0

sin 160−sin 20=?

$$\mathrm{sin}\:\mathrm{160}−\mathrm{sin}\:\mathrm{20}=? \\ $$

Question Number 143638 Answers: 0 Comments: 2

......Calculus.... 𝛗:=^? ∫_0 ^( 1) ((ln(1−x)ln(x)(ln(((1−x)/x))))/x) dx m.n....

$$\:\:\:\:\:\:\:\:\:\:......{Calculus}.... \\ $$$$\boldsymbol{\phi}:\overset{?} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right){ln}\left({x}\right)\left({ln}\left(\frac{\mathrm{1}−{x}}{{x}}\right)\right)}{{x}}\:{dx} \\ $$$$\:\:{m}.{n}.... \\ $$$$ \\ $$

Question Number 143630 Answers: 1 Comments: 1

prove that if a and c are odd integers then ab+bc is even for every integer b?

$${prove}\:{that}\:{if}\:{a}\:{and}\:{c}\:{are}\:{odd}\:{integers} \\ $$$${then}\:{ab}+{bc}\:{is}\:{even}\:{for}\:{every}\:{integer}\:{b}? \\ $$

Question Number 143628 Answers: 1 Comments: 0

∫_x ^∝ t^(α−1) e^(it) dt=??

$$\int_{{x}} ^{\propto} {t}^{\alpha−\mathrm{1}} {e}^{{it}} {dt}=?? \\ $$

Question Number 143627 Answers: 2 Comments: 0

Question Number 143635 Answers: 1 Comments: 0

Question Number 143633 Answers: 1 Comments: 0

Question Number 143624 Answers: 1 Comments: 0

∫_0 ^( ∞) z^2 e^(1/z) dz

$$\int_{\mathrm{0}} ^{\:\infty} {z}^{\mathrm{2}} {e}^{\frac{\mathrm{1}}{{z}}} {dz} \\ $$

Question Number 143622 Answers: 1 Comments: 0

∫_0 ^∝ e^(2arctg(t^2 )) dt

$$\int_{\mathrm{0}} ^{\propto} {e}^{\mathrm{2}{arctg}\left({t}^{\mathrm{2}} \right)} {dt} \\ $$

Question Number 143794 Answers: 0 Comments: 3

Prove 3^(111) +1⋮223

$$\mathrm{Prove}\:\:\:\:\:\:\:\:\:\mathrm{3}^{\mathrm{111}} +\mathrm{1}\vdots\mathrm{223} \\ $$

Question Number 143609 Answers: 1 Comments: 0

Prove that:: Ω:=∫_0 ^( 1) ((ln^2 (1−x).ln(x))/x)dx=((−1)/2) ζ (4 ) Without using the “Beta function” m.n

$$\:\:\: \\ $$$$\:{Prove}\:{that}:: \\ $$$$\:\:\Omega:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}\right).{ln}\left({x}\right)}{{x}}{dx}=\frac{−\mathrm{1}}{\mathrm{2}}\:\zeta\:\left(\mathrm{4}\:\right) \\ $$$${Without}\:{using}\:{the}\:``{Beta}\:{function}'' \\ $$$$\:\:{m}.{n} \\ $$

Question Number 143606 Answers: 1 Comments: 0

Question Number 143603 Answers: 2 Comments: 0

.....Calculus..... Ω:=Σ_(n=1) ^∞ (1/(n^k (1+n))) (k≥ 2) ......

$$\:\:\:\:\:\:\:\:\:\:\:\:\:.....{Calculus}..... \\ $$$$\:\:\:\:\:\:\:\:\Omega:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{{k}} \left(\mathrm{1}+{n}\right)}\:\:\:\left({k}\geqslant\:\mathrm{2}\right)\:...... \\ $$

Question Number 143602 Answers: 2 Comments: 1

Question Number 143598 Answers: 3 Comments: 2

Pg 744 Pg 745 Pg 746 Pg 747 Pg 748 Pg 749 Pg 750 Pg 751 Pg 752 Pg 753

Contact: info@tinkutara.com