Question and Answers Forum

All Questions Topic List

AllQuestion and Answers: Page 732

Question Number 145615 Answers: 0 Comments: 2

Let a,b,c > 0 and abc = 1. Prove that (a^3 /((a+1)^2 ))+(b^3 /((b+1)^2 ))+(c^3 /((c+1)^2 )) ≥((a+b+c)/4)

$$\mathrm{Let}\:{a},{b},{c}\:>\:\mathrm{0}\:\mathrm{and}\:{abc}\:=\:\mathrm{1}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{a}^{\mathrm{3}} }{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{b}^{\mathrm{3}} }{\left({b}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{c}^{\mathrm{3}} }{\left({c}+\mathrm{1}\right)^{\mathrm{2}} }\:\geqslant\frac{{a}+{b}+{c}}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

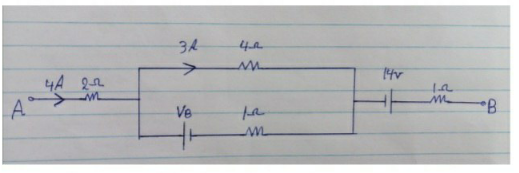
Question Number 145602 Answers: 5 Comments: 0

.....Advanced .........Calculus..... Q:: Find the value of :: determinant ((( i :: 𝛗 := ∫_0 ^( 1) Ln ( Γ ( 2 + x ) )dx = ? )),(( ii :: Ω := Σ_(n=1) ^∞ (( 1)/( n ( 2n + 3 ))) = ?))) .....m.n.july.1970..... ■

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....\mathrm{Advanced}\:.........\mathrm{Calculus}..... \\ $$$$\:\:\:\mathrm{Q}::\:\:\:\:\:\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\::: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\begin{array}{|c|c|}{\:{i}\:::\:\:\:\boldsymbol{\phi}\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{Ln}\:\left(\:\Gamma\:\left(\:\mathrm{2}\:+\:{x}\:\right)\:\right){dx}\:=\:?\:\:\:\:}\\{\:{ii}\:::\:\:\:\Omega\::=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\:\mathrm{1}}{\:{n}\:\left(\:\mathrm{2}{n}\:+\:\mathrm{3}\:\right)}\:=\:?}\\\hline\end{array} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....{m}.{n}.{july}.\mathrm{1970}.....\:\:\:\:\blacksquare \\ $$$$ \\ $$

Question Number 145626 Answers: 0 Comments: 2

Question Number 145588 Answers: 3 Comments: 0

Question Number 145583 Answers: 0 Comments: 0

une urne contient N boules dont M boules blanches et N−M boule noires on tire successivement et sans remise n boules de l′urne. soit A_i :′′prelever une boules noires au ieme tirage′′ calculer P(A_i )

$${une}\:{urne}\:{contient}\:{N}\:{boules}\:{dont} \\ $$$${M}\:{boules}\:{blanches}\:{et}\:{N}−{M}\:{boule}\:{noires} \\ $$$${on}\:{tire}\:{successivement}\:{et}\:{sans}\:{remise} \\ $$$${n}\:{boules}\:{de}\:{l}'{urne}. \\ $$$${soit}\:{A}_{{i}} :''{prelever}\:{une}\:{boules}\:{noires}\:{au}\:{ieme} \\ $$$${tirage}'' \\ $$$${calculer}\:{P}\left({A}_{{i}} \right) \\ $$

Question Number 145580 Answers: 0 Comments: 1

Question Number 145578 Answers: 1 Comments: 0

y′′_y=xsin2x solve the differential eqn..

$${y}''\_{y}={xsin}\mathrm{2}{x} \\ $$$${solve}\:{the}\:{differential}\:{eqn}.. \\ $$

Question Number 145577 Answers: 2 Comments: 1

Question Number 145575 Answers: 2 Comments: 0

Question Number 145573 Answers: 1 Comments: 0

Question Number 145609 Answers: 1 Comments: 1

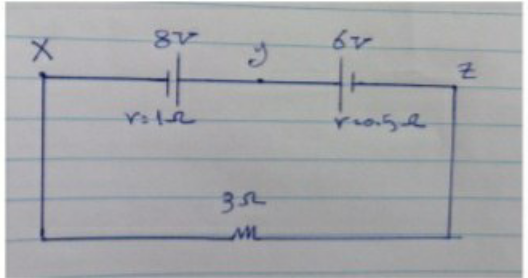
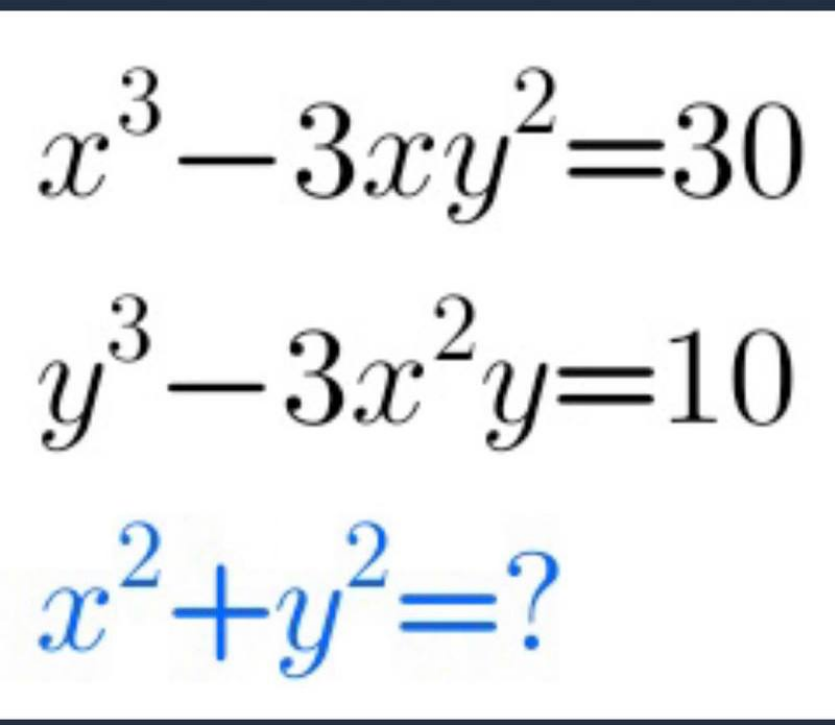
Question Number 145571 Answers: 0 Comments: 0

Question Number 145634 Answers: 2 Comments: 0

let s(x)=Σ_(n=1) ^∞ (((−1)^n )/((2x^2 +2x(√(1+x^2 ))+1)^n )) 1) explicite s(x) 2) calculate ∫_0 ^1 s(x)dx

$$\mathrm{let}\:\mathrm{s}\left(\mathrm{x}\right)=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{2x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{n}} } \\ $$$$\left.\mathrm{1}\right)\:\mathrm{explicite}\:\mathrm{s}\left(\mathrm{x}\right) \\ $$$$\left.\mathrm{2}\right)\:\mathrm{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{s}\left(\mathrm{x}\right)\mathrm{dx} \\ $$

Question Number 145633 Answers: 0 Comments: 0

find ∫_0 ^1 e^(−x) (√(1+x^2 ))dx (approximat value)

$$\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{e}^{−\mathrm{x}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:\left(\mathrm{approximat}\:\mathrm{value}\right) \\ $$

Question Number 145654 Answers: 2 Comments: 0

4cosy−3secy=2tany Find y

$$\mathrm{4}{cosy}−\mathrm{3}{secy}=\mathrm{2}{tany} \\ $$$${Find}\:{y} \\ $$

Question Number 146212 Answers: 1 Comments: 0

K=∫(1/( (√(1+x^3 ))))dx

$$\mathrm{K}=\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }}\mathrm{dx} \\ $$

Question Number 145636 Answers: 2 Comments: 0

calculate ∫_0 ^∞ ((arctanx)/((1+x^2 )^2 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctanx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 145635 Answers: 0 Comments: 0

calculate ∫_0 ^∞ ((arctan(3x^2 ))/(1+x^2 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctan}\left(\mathrm{3x}^{\mathrm{2}} \right)}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 145557 Answers: 1 Comments: 0

Question Number 145549 Answers: 1 Comments: 0

Find the equation of the asymptotes to the curve y = f(x) where f(x) = ln(((x+3)/(x−1))) .

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{asymptotes}\:\mathrm{to}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\:{y}\:=\:{f}\left({x}\right)\:\mathrm{where}\:{f}\left({x}\right)\:=\:\mathrm{ln}\left(\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\right)\:.\: \\ $$

Question Number 145548 Answers: 2 Comments: 0

if 3^x =24 and 2^y =36 find (4^((x-1)∙y) /4^x ) = ?

$${if}\:\:\mathrm{3}^{\boldsymbol{{x}}} =\mathrm{24}\:\:{and}\:\:\mathrm{2}^{\boldsymbol{{y}}} =\mathrm{36} \\ $$$${find}\:\:\:\frac{\mathrm{4}^{\left(\boldsymbol{{x}}-\mathrm{1}\right)\centerdot\boldsymbol{{y}}} }{\mathrm{4}^{\boldsymbol{{x}}} }\:=\:? \\ $$

Question Number 145547 Answers: 1 Comments: 0

I_(m,n) = ∫_0 ^1 (1−x^m )^n dx Show that I_(m,n) (mn+1) = I_(m,n−1)

$${I}_{{m},{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{{m}} \right)^{{n}} {dx} \\ $$$$\mathrm{Show}\:\mathrm{that}\:{I}_{{m},{n}} \left({mn}+\mathrm{1}\right)\:=\:{I}_{{m},{n}−\mathrm{1}} \\ $$

Question Number 145534 Answers: 1 Comments: 0

Question Number 145531 Answers: 3 Comments: 0

lim_(n→∞) sin^2 π (√(n^2 +n)) = ?

$$\underset{{n}\rightarrow\infty} {{lim}sin}^{\mathrm{2}} \pi\:\sqrt{{n}^{\mathrm{2}} +{n}}\:=\:? \\ $$

Question Number 145530 Answers: 1 Comments: 0

((1/2) + ((∣a∣ + ∣b∣)/(∣a + b∣)))_(min) = ?

$$\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mid{a}\mid\:+\:\mid{b}\mid}{\mid{a}\:+\:{b}\mid}\right)_{\boldsymbol{{min}}} =\:? \\ $$

Question Number 145528 Answers: 0 Comments: 0

State the asymptotes of the curve y^2 = ((3x^2 )/(x−4))

$$\mathrm{State}\:\mathrm{the}\:\mathrm{asymptotes}\:\mathrm{of}\:\mathrm{the}\:\mathrm{curve}\: \\ $$$$\:{y}^{\mathrm{2}} \:=\:\frac{\mathrm{3}{x}^{\mathrm{2}} }{{x}−\mathrm{4}} \\ $$

Pg 727 Pg 728 Pg 729 Pg 730 Pg 731 Pg 732 Pg 733 Pg 734 Pg 735 Pg 736

Terms of Service

Contact: info@tinkutara.com