Question and Answers Forum

AllQuestion and Answers: Page 729

Question Number 145525 Answers: 1 Comments: 0

Question Number 145522 Answers: 1 Comments: 0

montrer que l′ensemble des suites reelle qui verifie la relation ∀n∈N aU_(n+2) +bU_(n+1) +cU_n =0 (1) est un espace vectoriel de dimension 2 et determiner une base

$${montrer}\:{que}\:{l}'{ensemble}\:{des}\:{suites}\:{reelle}\:{qui} \\ $$$${verifie}\:{la}\:{relation}\:\forall{n}\in\mathbb{N} \\ $$$${aU}_{{n}+\mathrm{2}} +{bU}_{{n}+\mathrm{1}} +{cU}_{{n}} =\mathrm{0}\:\left(\mathrm{1}\right)\:\:{est}\:{un}\:{espace} \\ $$$${vectoriel}\:{de}\:{dimension}\:\mathrm{2} \\ $$$${et}\:{determiner}\:{une}\:{base}\: \\ $$$$ \\ $$

Question Number 145519 Answers: 0 Comments: 1

Question Number 145517 Answers: 1 Comments: 0

Find the center of mass for the thin plate bounded by curves g(x)=(x/2) and f(x)=(√x) , 0≤x≤1 .

$${Find}\:{the}\:{center}\:{of}\:{mass}\:{for}\: \\ $$$${the}\:{thin}\:{plate}\:{bounded}\:{by}\: \\ $$$${curves}\:{g}\left({x}\right)=\frac{{x}}{\mathrm{2}}\:{and}\:{f}\left({x}\right)=\sqrt{{x}} \\ $$$$,\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:. \\ $$

Question Number 145516 Answers: 2 Comments: 0

f(x+y)=f(x)+f(y)+xy for all x and y fromR and f(4)=10 calculate f(1319)

$$\mathrm{f}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{y}\right)+\mathrm{xy}\:\mathrm{for}\:\mathrm{all}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{fromR} \\ $$$$\mathrm{and}\:\mathrm{f}\left(\mathrm{4}\right)=\mathrm{10}\:\:\mathrm{calculate}\:\mathrm{f}\left(\mathrm{1319}\right) \\ $$

Question Number 145515 Answers: 1 Comments: 0

f(x)=e^(−x) arctan((3/x)) 1)find f^((n)) (3) 2)give taylor developpement for f at x_0 =3 3)find ∫_0 ^∞ f(x)dx

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{−\mathrm{x}} \mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right) \\ $$$$\left.\mathrm{1}\right)\mathrm{find}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{3}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{give}\:\mathrm{taylor}\:\mathrm{developpement}\:\mathrm{for}\:\mathrm{f}\:\mathrm{at}\:\mathrm{x}_{\mathrm{0}} =\mathrm{3} \\ $$$$\left.\mathrm{3}\right)\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$

Question Number 145514 Answers: 1 Comments: 0

let A_n =∫_0 ^(2nπ) (dx/((2+cosx)^2 )) explicit A_n and determine nature of serie Σ A_n

$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{2n}\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{2}+\mathrm{cosx}\right)^{\mathrm{2}} } \\ $$$$\mathrm{explicit}\:\mathrm{A}_{\mathrm{n}} \:\mathrm{and}\:\mathrm{determine}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{serie}\:\Sigma\:\mathrm{A}_{\mathrm{n}} \\ $$

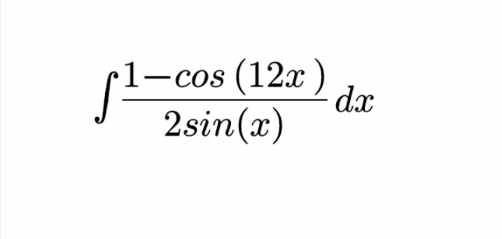
Question Number 145499 Answers: 2 Comments: 0

(1/2) - (1/4) + (1/8) - (1/(16)) + ... - (1/(256)) = ((z+1)/(256)) find z=?

$$\frac{\mathrm{1}}{\mathrm{2}}\:-\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{1}}{\mathrm{8}}\:-\:\frac{\mathrm{1}}{\mathrm{16}}\:+\:...\:-\:\frac{\mathrm{1}}{\mathrm{256}}\:=\:\frac{\boldsymbol{{z}}+\mathrm{1}}{\mathrm{256}} \\ $$$${find}\:\:\boldsymbol{{z}}=? \\ $$

Question Number 145491 Answers: 2 Comments: 1

Question Number 145489 Answers: 2 Comments: 3

Question Number 145487 Answers: 2 Comments: 1

Question Number 145474 Answers: 0 Comments: 0

R C Classes M.M.−30 10th−Maths Test Time Duration:40min. If the given expression is an AP then write the common difference and write three more terms Q.1) 3, 3+(√(2,)) 3+2(√2), 3+3(√2)........ Q.2) (√2), (√8) ,(√(18)),(√(32)),...... Q.3) Derive the formula a_n = a+(n−1)d Q.4) Check whether 301 is a term of the list of numbers 5, 11, 17, 23,......... Q.5) a=−18.9, d= 2.5, a_n = 3.6 find a Q.6) In the following AP, find the missing terms in the boxes.

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{R}\:\mathrm{C}\:\mathrm{Classes}\: \\ $$$$\:\:\mathrm{M}.\mathrm{M}.−\mathrm{30}\:\:\:\:\mathrm{10th}−\mathrm{Maths}\:\mathrm{Test}\:\:\:\mathrm{Time}\:\mathrm{Duration}:\mathrm{40min}. \\ $$$$\:\:\mathrm{If}\:\:\mathrm{the}\:\:\mathrm{given}\:\mathrm{expression}\:\mathrm{is}\:\mathrm{an}\:\mathrm{AP}\:\mathrm{then} \\ $$$$\:\mathrm{write}\:\mathrm{the}\:\mathrm{common}\:\mathrm{difference}\:\mathrm{and}\:\mathrm{write}\:\:\:\mathrm{three}\:\mathrm{more}\:\mathrm{terms} \\ $$$$\left.\:\:\:\mathrm{Q}.\mathrm{1}\right)\:\:\mathrm{3},\:\mathrm{3}+\sqrt{\mathrm{2},}\:\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}},\:\mathrm{3}+\mathrm{3}\sqrt{\mathrm{2}}........ \\ $$$$\: \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{2}\right)\:\:\sqrt{\mathrm{2}},\:\sqrt{\mathrm{8}}\:,\sqrt{\mathrm{18}},\sqrt{\mathrm{32}},...... \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{3}\right)\:\:\mathrm{Derive}\:\mathrm{the}\:\mathrm{formula}\:\:\mathrm{a}_{\mathrm{n}} =\:\mathrm{a}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{d} \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{4}\right)\:\:\mathrm{Check}\:\mathrm{whether}\:\mathrm{301}\:\mathrm{is}\:\mathrm{a}\:\mathrm{term}\:\mathrm{of}\:\mathrm{the}\:\mathrm{list}\:\mathrm{of}\:\mathrm{numbers} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5},\:\mathrm{11},\:\mathrm{17},\:\mathrm{23},......... \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{5}\right)\:\:\mathrm{a}=−\mathrm{18}.\mathrm{9},\:\:\mathrm{d}=\:\mathrm{2}.\mathrm{5},\:\mathrm{a}_{\mathrm{n}} =\:\mathrm{3}.\mathrm{6}\:\:\mathrm{find}\:\boldsymbol{\mathrm{a}} \\ $$$$\left.\:\:\boldsymbol{\mathrm{Q}}.\mathrm{6}\right)\:\:\mathrm{In}\:\mathrm{the}\:\mathrm{following}\:\mathrm{AP},\:\mathrm{find}\:\mathrm{the}\:\mathrm{missing}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the}\:\mathrm{boxes}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Question Number 145468 Answers: 1 Comments: 0

Question Number 145467 Answers: 1 Comments: 0

Question Number 145463 Answers: 1 Comments: 0

Question Number 145483 Answers: 2 Comments: 1

Question Number 145456 Answers: 1 Comments: 0

∫sin(x^2 +2)dx

$$\int\boldsymbol{{sin}}\left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{2}\right)\boldsymbol{{dx}} \\ $$

Question Number 145451 Answers: 1 Comments: 0

Σ_(n=1) ^∞ (−1)^(n−1) ((30^(2n−1) )/((2n−1)!))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{\mathrm{30}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)!} \\ $$

Question Number 145450 Answers: 2 Comments: 0

Question Number 145449 Answers: 1 Comments: 0

Question Number 145444 Answers: 1 Comments: 0

(1/2) - (3/4) + (7/8) - ((15)/(16)) + ... = ?

$$\frac{\mathrm{1}}{\mathrm{2}}\:-\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{7}}{\mathrm{8}}\:-\:\frac{\mathrm{15}}{\mathrm{16}}\:+\:...\:=\:? \\ $$

Question Number 145443 Answers: 2 Comments: 0

The roots of the equation 2x^2 +px+q=0 are 2α+β and α+2β. Find the values of p and q

$${The}\:{roots}\:{of}\:{the}\:{equation} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\:\:{are}\:\mathrm{2}\alpha+\beta\:\:{and} \\ $$$$\alpha+\mathrm{2}\beta.\:{Find}\:{the}\:{values}\:{of}\:{p}\:{and}\:{q} \\ $$

Question Number 145442 Answers: 1 Comments: 0

soit z∈C montrer que cos(z) et sin (z) ne sont pas bornees que vaut sin^2 (z)+cos^2 (z)=??

$${soit}\:{z}\in\mathbb{C}\:{montrer}\:{que}\:{cos}\left({z}\right)\:{et}\:{sin}\:\left({z}\right) \\ $$$${ne}\:{sont}\:{pas}\:{bornees} \\ $$$${que}\:{vaut}\:{sin}^{\mathrm{2}} \left({z}\right)+{cos}^{\mathrm{2}} \left({z}\right)=?? \\ $$

Question Number 145437 Answers: 0 Comments: 0

original length of the iron rod=175.65 % increase=6(1/3)%×175.65 =((19)/3)×(1/(100))×175.65 =((19×175.65)/(3×100))=((3337.35)/(300))=11.1245 new length=original length+increased length =175.65+11.1245 =186.7745cm solution by CASIO.....

$${original}\:{length}\:{of}\:{the}\:{iron}\:{rod}=\mathrm{175}.\mathrm{65} \\ $$$$\%\:{increase}=\mathrm{6}\frac{\mathrm{1}}{\mathrm{3}}\%×\mathrm{175}.\mathrm{65} \\ $$$$=\frac{\mathrm{19}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{100}}×\mathrm{175}.\mathrm{65} \\ $$$$=\frac{\mathrm{19}×\mathrm{175}.\mathrm{65}}{\mathrm{3}×\mathrm{100}}=\frac{\mathrm{3337}.\mathrm{35}}{\mathrm{300}}=\mathrm{11}.\mathrm{1245} \\ $$$${new}\:{length}={original}\:{length}+{increased}\:{length} \\ $$$$=\mathrm{175}.\mathrm{65}+\mathrm{11}.\mathrm{1245} \\ $$$$=\mathrm{186}.\mathrm{7745}{cm} \\ $$$${solution}\:{by}\:{CASIO}..... \\ $$$$ \\ $$

Question Number 145436 Answers: 0 Comments: 2

Question Number 145553 Answers: 1 Comments: 0

Pg 724 Pg 725 Pg 726 Pg 727 Pg 728 Pg 729 Pg 730 Pg 731 Pg 732 Pg 733

Contact: info@tinkutara.com