Question and Answers Forum

AllQuestion and Answers: Page 727

Question Number 145557 Answers: 1 Comments: 0

Question Number 145549 Answers: 1 Comments: 0

Find the equation of the asymptotes to the curve y = f(x) where f(x) = ln(((x+3)/(x−1))) .

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{asymptotes}\:\mathrm{to}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\:{y}\:=\:{f}\left({x}\right)\:\mathrm{where}\:{f}\left({x}\right)\:=\:\mathrm{ln}\left(\frac{{x}+\mathrm{3}}{{x}−\mathrm{1}}\right)\:.\: \\ $$

Question Number 145548 Answers: 2 Comments: 0

if 3^x =24 and 2^y =36 find (4^((x-1)∙y) /4^x ) = ?

$${if}\:\:\mathrm{3}^{\boldsymbol{{x}}} =\mathrm{24}\:\:{and}\:\:\mathrm{2}^{\boldsymbol{{y}}} =\mathrm{36} \\ $$$${find}\:\:\:\frac{\mathrm{4}^{\left(\boldsymbol{{x}}-\mathrm{1}\right)\centerdot\boldsymbol{{y}}} }{\mathrm{4}^{\boldsymbol{{x}}} }\:=\:? \\ $$

Question Number 145547 Answers: 1 Comments: 0

I_(m,n) = ∫_0 ^1 (1−x^m )^n dx Show that I_(m,n) (mn+1) = I_(m,n−1)

$${I}_{{m},{n}} \:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{{m}} \right)^{{n}} {dx} \\ $$$$\mathrm{Show}\:\mathrm{that}\:{I}_{{m},{n}} \left({mn}+\mathrm{1}\right)\:=\:{I}_{{m},{n}−\mathrm{1}} \\ $$

Question Number 145534 Answers: 1 Comments: 0

Question Number 145531 Answers: 3 Comments: 0

lim_(n→∞) sin^2 π (√(n^2 +n)) = ?

$$\underset{{n}\rightarrow\infty} {{lim}sin}^{\mathrm{2}} \pi\:\sqrt{{n}^{\mathrm{2}} +{n}}\:=\:? \\ $$

Question Number 145530 Answers: 1 Comments: 0

((1/2) + ((∣a∣ + ∣b∣)/(∣a + b∣)))_(min) = ?

$$\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mid{a}\mid\:+\:\mid{b}\mid}{\mid{a}\:+\:{b}\mid}\right)_{\boldsymbol{{min}}} =\:? \\ $$

Question Number 145528 Answers: 0 Comments: 0

State the asymptotes of the curve y^2 = ((3x^2 )/(x−4))

$$\mathrm{State}\:\mathrm{the}\:\mathrm{asymptotes}\:\mathrm{of}\:\mathrm{the}\:\mathrm{curve}\: \\ $$$$\:{y}^{\mathrm{2}} \:=\:\frac{\mathrm{3}{x}^{\mathrm{2}} }{{x}−\mathrm{4}} \\ $$

Question Number 145525 Answers: 1 Comments: 0

Question Number 145522 Answers: 1 Comments: 0

montrer que l′ensemble des suites reelle qui verifie la relation ∀n∈N aU_(n+2) +bU_(n+1) +cU_n =0 (1) est un espace vectoriel de dimension 2 et determiner une base

$${montrer}\:{que}\:{l}'{ensemble}\:{des}\:{suites}\:{reelle}\:{qui} \\ $$$${verifie}\:{la}\:{relation}\:\forall{n}\in\mathbb{N} \\ $$$${aU}_{{n}+\mathrm{2}} +{bU}_{{n}+\mathrm{1}} +{cU}_{{n}} =\mathrm{0}\:\left(\mathrm{1}\right)\:\:{est}\:{un}\:{espace} \\ $$$${vectoriel}\:{de}\:{dimension}\:\mathrm{2} \\ $$$${et}\:{determiner}\:{une}\:{base}\: \\ $$$$ \\ $$

Question Number 145519 Answers: 0 Comments: 1

Question Number 145517 Answers: 1 Comments: 0

Find the center of mass for the thin plate bounded by curves g(x)=(x/2) and f(x)=(√x) , 0≤x≤1 .

$${Find}\:{the}\:{center}\:{of}\:{mass}\:{for}\: \\ $$$${the}\:{thin}\:{plate}\:{bounded}\:{by}\: \\ $$$${curves}\:{g}\left({x}\right)=\frac{{x}}{\mathrm{2}}\:{and}\:{f}\left({x}\right)=\sqrt{{x}} \\ $$$$,\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:. \\ $$

Question Number 145516 Answers: 2 Comments: 0

f(x+y)=f(x)+f(y)+xy for all x and y fromR and f(4)=10 calculate f(1319)

$$\mathrm{f}\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{y}\right)+\mathrm{xy}\:\mathrm{for}\:\mathrm{all}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{fromR} \\ $$$$\mathrm{and}\:\mathrm{f}\left(\mathrm{4}\right)=\mathrm{10}\:\:\mathrm{calculate}\:\mathrm{f}\left(\mathrm{1319}\right) \\ $$

Question Number 145515 Answers: 1 Comments: 0

f(x)=e^(−x) arctan((3/x)) 1)find f^((n)) (3) 2)give taylor developpement for f at x_0 =3 3)find ∫_0 ^∞ f(x)dx

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{−\mathrm{x}} \mathrm{arctan}\left(\frac{\mathrm{3}}{\mathrm{x}}\right) \\ $$$$\left.\mathrm{1}\right)\mathrm{find}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{3}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{give}\:\mathrm{taylor}\:\mathrm{developpement}\:\mathrm{for}\:\mathrm{f}\:\mathrm{at}\:\mathrm{x}_{\mathrm{0}} =\mathrm{3} \\ $$$$\left.\mathrm{3}\right)\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$

Question Number 145514 Answers: 1 Comments: 0

let A_n =∫_0 ^(2nπ) (dx/((2+cosx)^2 )) explicit A_n and determine nature of serie Σ A_n

$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{2n}\pi} \:\frac{\mathrm{dx}}{\left(\mathrm{2}+\mathrm{cosx}\right)^{\mathrm{2}} } \\ $$$$\mathrm{explicit}\:\mathrm{A}_{\mathrm{n}} \:\mathrm{and}\:\mathrm{determine}\:\mathrm{nature}\:\mathrm{of}\:\mathrm{serie}\:\Sigma\:\mathrm{A}_{\mathrm{n}} \\ $$

Question Number 145499 Answers: 2 Comments: 0

(1/2) - (1/4) + (1/8) - (1/(16)) + ... - (1/(256)) = ((z+1)/(256)) find z=?

$$\frac{\mathrm{1}}{\mathrm{2}}\:-\:\frac{\mathrm{1}}{\mathrm{4}}\:+\:\frac{\mathrm{1}}{\mathrm{8}}\:-\:\frac{\mathrm{1}}{\mathrm{16}}\:+\:...\:-\:\frac{\mathrm{1}}{\mathrm{256}}\:=\:\frac{\boldsymbol{{z}}+\mathrm{1}}{\mathrm{256}} \\ $$$${find}\:\:\boldsymbol{{z}}=? \\ $$

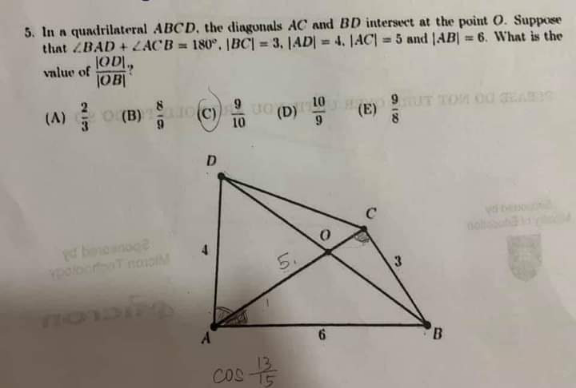
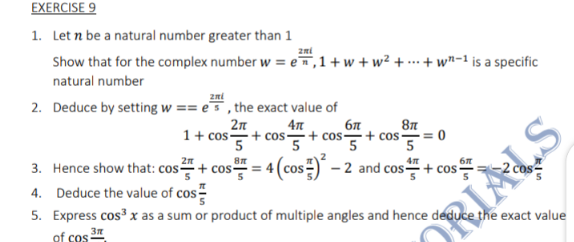
Question Number 145491 Answers: 2 Comments: 1

Question Number 145489 Answers: 2 Comments: 3

Question Number 145487 Answers: 2 Comments: 1

Question Number 145474 Answers: 0 Comments: 0

R C Classes M.M.−30 10th−Maths Test Time Duration:40min. If the given expression is an AP then write the common difference and write three more terms Q.1) 3, 3+(√(2,)) 3+2(√2), 3+3(√2)........ Q.2) (√2), (√8) ,(√(18)),(√(32)),...... Q.3) Derive the formula a_n = a+(n−1)d Q.4) Check whether 301 is a term of the list of numbers 5, 11, 17, 23,......... Q.5) a=−18.9, d= 2.5, a_n = 3.6 find a Q.6) In the following AP, find the missing terms in the boxes.

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{R}\:\mathrm{C}\:\mathrm{Classes}\: \\ $$$$\:\:\mathrm{M}.\mathrm{M}.−\mathrm{30}\:\:\:\:\mathrm{10th}−\mathrm{Maths}\:\mathrm{Test}\:\:\:\mathrm{Time}\:\mathrm{Duration}:\mathrm{40min}. \\ $$$$\:\:\mathrm{If}\:\:\mathrm{the}\:\:\mathrm{given}\:\mathrm{expression}\:\mathrm{is}\:\mathrm{an}\:\mathrm{AP}\:\mathrm{then} \\ $$$$\:\mathrm{write}\:\mathrm{the}\:\mathrm{common}\:\mathrm{difference}\:\mathrm{and}\:\mathrm{write}\:\:\:\mathrm{three}\:\mathrm{more}\:\mathrm{terms} \\ $$$$\left.\:\:\:\mathrm{Q}.\mathrm{1}\right)\:\:\mathrm{3},\:\mathrm{3}+\sqrt{\mathrm{2},}\:\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}},\:\mathrm{3}+\mathrm{3}\sqrt{\mathrm{2}}........ \\ $$$$\: \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{2}\right)\:\:\sqrt{\mathrm{2}},\:\sqrt{\mathrm{8}}\:,\sqrt{\mathrm{18}},\sqrt{\mathrm{32}},...... \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{3}\right)\:\:\mathrm{Derive}\:\mathrm{the}\:\mathrm{formula}\:\:\mathrm{a}_{\mathrm{n}} =\:\mathrm{a}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{d} \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{4}\right)\:\:\mathrm{Check}\:\mathrm{whether}\:\mathrm{301}\:\mathrm{is}\:\mathrm{a}\:\mathrm{term}\:\mathrm{of}\:\mathrm{the}\:\mathrm{list}\:\mathrm{of}\:\mathrm{numbers} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5},\:\mathrm{11},\:\mathrm{17},\:\mathrm{23},......... \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{5}\right)\:\:\mathrm{a}=−\mathrm{18}.\mathrm{9},\:\:\mathrm{d}=\:\mathrm{2}.\mathrm{5},\:\mathrm{a}_{\mathrm{n}} =\:\mathrm{3}.\mathrm{6}\:\:\mathrm{find}\:\boldsymbol{\mathrm{a}} \\ $$$$\left.\:\:\boldsymbol{\mathrm{Q}}.\mathrm{6}\right)\:\:\mathrm{In}\:\mathrm{the}\:\mathrm{following}\:\mathrm{AP},\:\mathrm{find}\:\mathrm{the}\:\mathrm{missing}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the}\:\mathrm{boxes}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Question Number 145468 Answers: 1 Comments: 0

Question Number 145467 Answers: 1 Comments: 0

Question Number 145463 Answers: 1 Comments: 0

Question Number 145483 Answers: 2 Comments: 1

Question Number 145456 Answers: 1 Comments: 0

∫sin(x^2 +2)dx

$$\int\boldsymbol{{sin}}\left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{2}\right)\boldsymbol{{dx}} \\ $$

Question Number 145451 Answers: 1 Comments: 0

Σ_(n=1) ^∞ (−1)^(n−1) ((30^(2n−1) )/((2n−1)!))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{\mathrm{30}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)!} \\ $$

Pg 722 Pg 723 Pg 724 Pg 725 Pg 726 Pg 727 Pg 728 Pg 729 Pg 730 Pg 731

Contact: info@tinkutara.com