
AllQuestion and Answers: Page 725
Question Number 146987 Answers: 1 Comments: 0

Question Number 146979 Answers: 1 Comments: 1
Question Number 146977 Answers: 2 Comments: 0
Question Number 146975 Answers: 1 Comments: 0
Question Number 146964 Answers: 1 Comments: 0
Question Number 146962 Answers: 1 Comments: 0

Question Number 146961 Answers: 1 Comments: 0
$$\sqrt{{sin}\left({x}\right)}\:\centerdot\:{cos}\left({x}\right)\:<\:\mathrm{0} \\ $$
Question Number 146960 Answers: 2 Comments: 0

Question Number 146959 Answers: 1 Comments: 0
$$\int{ln}\left(\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}\right){dx} \\ $$
Question Number 147764 Answers: 1 Comments: 0

Question Number 146943 Answers: 3 Comments: 0
Question Number 146938 Answers: 0 Comments: 0
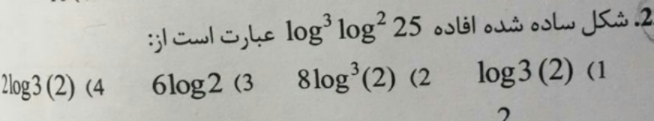
Question Number 146936 Answers: 3 Comments: 0
Question Number 146933 Answers: 0 Comments: 0
Question Number 146929 Answers: 1 Comments: 5

Question Number 146927 Answers: 1 Comments: 0

Question Number 146926 Answers: 1 Comments: 0

Question Number 146924 Answers: 1 Comments: 0
Question Number 146923 Answers: 1 Comments: 0
Question Number 146914 Answers: 2 Comments: 0
Question Number 146913 Answers: 1 Comments: 0
Question Number 146906 Answers: 0 Comments: 0

Question Number 147078 Answers: 0 Comments: 1
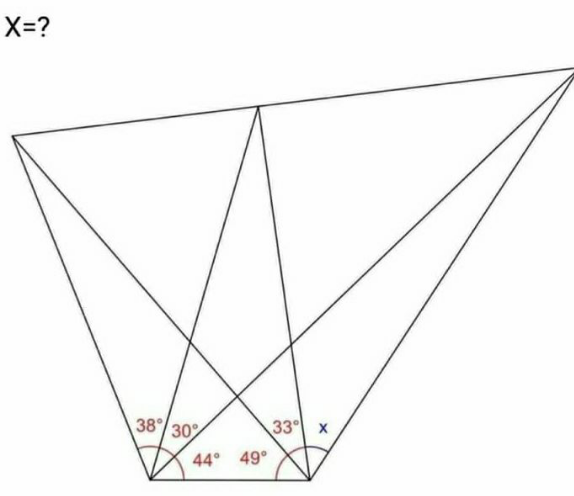
Question Number 146904 Answers: 0 Comments: 0
Question Number 146902 Answers: 1 Comments: 0
Question Number 146901 Answers: 1 Comments: 0
Pg 720 Pg 721 Pg 722 Pg 723 Pg 724 Pg 725 Pg 726 Pg 727 Pg 728 Pg 729
