Question and Answers Forum

AllQuestion and Answers: Page 723

Question Number 145474 Answers: 0 Comments: 0

R C Classes M.M.−30 10th−Maths Test Time Duration:40min. If the given expression is an AP then write the common difference and write three more terms Q.1) 3, 3+(√(2,)) 3+2(√2), 3+3(√2)........ Q.2) (√2), (√8) ,(√(18)),(√(32)),...... Q.3) Derive the formula a_n = a+(n−1)d Q.4) Check whether 301 is a term of the list of numbers 5, 11, 17, 23,......... Q.5) a=−18.9, d= 2.5, a_n = 3.6 find a Q.6) In the following AP, find the missing terms in the boxes.

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{R}\:\mathrm{C}\:\mathrm{Classes}\: \\ $$$$\:\:\mathrm{M}.\mathrm{M}.−\mathrm{30}\:\:\:\:\mathrm{10th}−\mathrm{Maths}\:\mathrm{Test}\:\:\:\mathrm{Time}\:\mathrm{Duration}:\mathrm{40min}. \\ $$$$\:\:\mathrm{If}\:\:\mathrm{the}\:\:\mathrm{given}\:\mathrm{expression}\:\mathrm{is}\:\mathrm{an}\:\mathrm{AP}\:\mathrm{then} \\ $$$$\:\mathrm{write}\:\mathrm{the}\:\mathrm{common}\:\mathrm{difference}\:\mathrm{and}\:\mathrm{write}\:\:\:\mathrm{three}\:\mathrm{more}\:\mathrm{terms} \\ $$$$\left.\:\:\:\mathrm{Q}.\mathrm{1}\right)\:\:\mathrm{3},\:\mathrm{3}+\sqrt{\mathrm{2},}\:\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}},\:\mathrm{3}+\mathrm{3}\sqrt{\mathrm{2}}........ \\ $$$$\: \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{2}\right)\:\:\sqrt{\mathrm{2}},\:\sqrt{\mathrm{8}}\:,\sqrt{\mathrm{18}},\sqrt{\mathrm{32}},...... \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{3}\right)\:\:\mathrm{Derive}\:\mathrm{the}\:\mathrm{formula}\:\:\mathrm{a}_{\mathrm{n}} =\:\mathrm{a}+\left(\mathrm{n}−\mathrm{1}\right)\mathrm{d} \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{4}\right)\:\:\mathrm{Check}\:\mathrm{whether}\:\mathrm{301}\:\mathrm{is}\:\mathrm{a}\:\mathrm{term}\:\mathrm{of}\:\mathrm{the}\:\mathrm{list}\:\mathrm{of}\:\mathrm{numbers} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5},\:\mathrm{11},\:\mathrm{17},\:\mathrm{23},......... \\ $$$$\left.\:\:\mathrm{Q}.\mathrm{5}\right)\:\:\mathrm{a}=−\mathrm{18}.\mathrm{9},\:\:\mathrm{d}=\:\mathrm{2}.\mathrm{5},\:\mathrm{a}_{\mathrm{n}} =\:\mathrm{3}.\mathrm{6}\:\:\mathrm{find}\:\boldsymbol{\mathrm{a}} \\ $$$$\left.\:\:\boldsymbol{\mathrm{Q}}.\mathrm{6}\right)\:\:\mathrm{In}\:\mathrm{the}\:\mathrm{following}\:\mathrm{AP},\:\mathrm{find}\:\mathrm{the}\:\mathrm{missing}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the}\:\mathrm{boxes}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Question Number 145468 Answers: 1 Comments: 0

Question Number 145467 Answers: 1 Comments: 0

Question Number 145463 Answers: 1 Comments: 0

Question Number 145483 Answers: 2 Comments: 1

Question Number 145456 Answers: 1 Comments: 0

∫sin(x^2 +2)dx

$$\int\boldsymbol{{sin}}\left(\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{2}\right)\boldsymbol{{dx}} \\ $$

Question Number 145451 Answers: 1 Comments: 0

Σ_(n=1) ^∞ (−1)^(n−1) ((30^(2n−1) )/((2n−1)!))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{\mathrm{30}^{\mathrm{2}{n}−\mathrm{1}} }{\left(\mathrm{2}{n}−\mathrm{1}\right)!} \\ $$

Question Number 145450 Answers: 2 Comments: 0

Question Number 145449 Answers: 1 Comments: 0

Question Number 145444 Answers: 1 Comments: 0

(1/2) - (3/4) + (7/8) - ((15)/(16)) + ... = ?

$$\frac{\mathrm{1}}{\mathrm{2}}\:-\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{7}}{\mathrm{8}}\:-\:\frac{\mathrm{15}}{\mathrm{16}}\:+\:...\:=\:? \\ $$

Question Number 145443 Answers: 2 Comments: 0

The roots of the equation 2x^2 +px+q=0 are 2α+β and α+2β. Find the values of p and q

$${The}\:{roots}\:{of}\:{the}\:{equation} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\:\:{are}\:\mathrm{2}\alpha+\beta\:\:{and} \\ $$$$\alpha+\mathrm{2}\beta.\:{Find}\:{the}\:{values}\:{of}\:{p}\:{and}\:{q} \\ $$

Question Number 145442 Answers: 1 Comments: 0

soit z∈C montrer que cos(z) et sin (z) ne sont pas bornees que vaut sin^2 (z)+cos^2 (z)=??

$${soit}\:{z}\in\mathbb{C}\:{montrer}\:{que}\:{cos}\left({z}\right)\:{et}\:{sin}\:\left({z}\right) \\ $$$${ne}\:{sont}\:{pas}\:{bornees} \\ $$$${que}\:{vaut}\:{sin}^{\mathrm{2}} \left({z}\right)+{cos}^{\mathrm{2}} \left({z}\right)=?? \\ $$

Question Number 145437 Answers: 0 Comments: 0

original length of the iron rod=175.65 % increase=6(1/3)%×175.65 =((19)/3)×(1/(100))×175.65 =((19×175.65)/(3×100))=((3337.35)/(300))=11.1245 new length=original length+increased length =175.65+11.1245 =186.7745cm solution by CASIO.....

$${original}\:{length}\:{of}\:{the}\:{iron}\:{rod}=\mathrm{175}.\mathrm{65} \\ $$$$\%\:{increase}=\mathrm{6}\frac{\mathrm{1}}{\mathrm{3}}\%×\mathrm{175}.\mathrm{65} \\ $$$$=\frac{\mathrm{19}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{100}}×\mathrm{175}.\mathrm{65} \\ $$$$=\frac{\mathrm{19}×\mathrm{175}.\mathrm{65}}{\mathrm{3}×\mathrm{100}}=\frac{\mathrm{3337}.\mathrm{35}}{\mathrm{300}}=\mathrm{11}.\mathrm{1245} \\ $$$${new}\:{length}={original}\:{length}+{increased}\:{length} \\ $$$$=\mathrm{175}.\mathrm{65}+\mathrm{11}.\mathrm{1245} \\ $$$$=\mathrm{186}.\mathrm{7745}{cm} \\ $$$${solution}\:{by}\:{CASIO}..... \\ $$$$ \\ $$

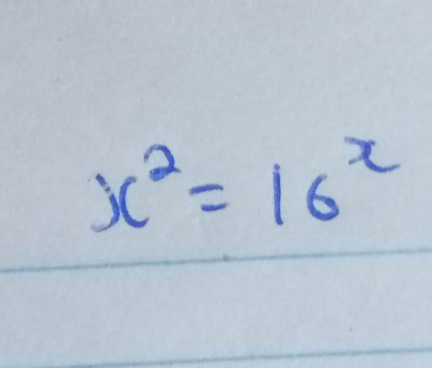
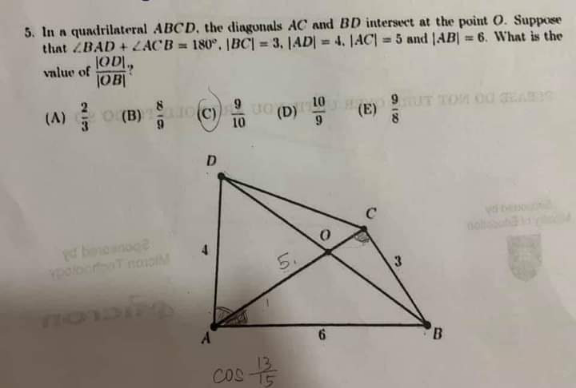
Question Number 145436 Answers: 0 Comments: 2

Question Number 145553 Answers: 1 Comments: 0

Question Number 145423 Answers: 2 Comments: 0

Question Number 145420 Answers: 1 Comments: 0

Developpement limite^ ge^ ne^ ralise^ au voisinnage de −∞ de g(x)=((√(1+x^2 ))/(1+x+(√(1+x^2 )))) et de^ duire une asymptote en −∞ ainsi que sa position relative par rapport a la courbe.

$$\mathrm{Developpement}\:\:\mathrm{limit}\acute {\mathrm{e}}\:\mathrm{g}\acute {\mathrm{e}n}\acute {\mathrm{e}ralis}\acute {\mathrm{e}}\:\mathrm{au}\: \\ $$$$\mathrm{voisinnage}\:\mathrm{de}\:−\infty\:\mathrm{de}\:\mathrm{g}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{et}\:\mathrm{d}\acute {\mathrm{e}duire}\:\mathrm{une}\:\mathrm{asymptote}\:\mathrm{en}\:−\infty\: \\ $$$$\mathrm{ainsi}\:\mathrm{que}\:\mathrm{sa}\:\mathrm{position}\:\mathrm{relative}\:\mathrm{par}\:\mathrm{rapport} \\ $$$$\mathrm{a}\:\mathrm{la}\:\mathrm{courbe}. \\ $$

Question Number 145459 Answers: 1 Comments: 0

prove (A − B)−C = A −(B ∪ C)

$${prove}\:\left({A}\:−\:{B}\right)−{C}\:=\:{A}\:−\left({B}\:\cup\:{C}\right) \\ $$

Question Number 145412 Answers: 1 Comments: 0

∫ln(cosx)dx=?

$$\:\:\:\:\int\mathrm{ln}\left(\mathrm{cosx}\right)\mathrm{dx}=? \\ $$

Question Number 145411 Answers: 1 Comments: 0

un espace vectoriel n′as un seul hyper-plan.. quelle est sa dimension.?

$$\mathrm{un}\:\mathrm{espace}\:\mathrm{vectoriel}\:\mathrm{n}'\mathrm{as}\:\mathrm{un}\:\mathrm{seul}\: \\ $$$$\mathrm{hyper}-\mathrm{plan}..\:\mathrm{quelle}\:\mathrm{est}\:\mathrm{sa}\:\mathrm{dimension}.? \\ $$

Question Number 145408 Answers: 0 Comments: 0

∫_0 ^x ⌊u⌋(⌊u⌋+1)f(u)du=Σ_(n=1) ^(⌊x⌋) n∫_n ^x f(u)du Prove that

$$\int_{\mathrm{0}} ^{{x}} \lfloor{u}\rfloor\left(\lfloor{u}\rfloor+\mathrm{1}\right){f}\left({u}\right){du}=\underset{{n}=\mathrm{1}} {\overset{\lfloor{x}\rfloor} {\sum}}{n}\int_{{n}} ^{{x}} {f}\left({u}\right){du}\:\: \\ $$$${Prove}\:{that} \\ $$

Question Number 145406 Answers: 2 Comments: 0

if log_a c+log_c b=2 ; log_b c+log_a c=0 find (1/(log_a b)) + (1/(log_b c)) + (1/(log_c a)) = ?

$${if}\:\:\boldsymbol{{log}}_{\boldsymbol{{a}}} \boldsymbol{{c}}+\boldsymbol{{log}}_{\boldsymbol{{c}}} \boldsymbol{{b}}=\mathrm{2}\:;\:\boldsymbol{{log}}_{\boldsymbol{{b}}} \boldsymbol{{c}}+\boldsymbol{{log}}_{\boldsymbol{{a}}} \boldsymbol{{c}}=\mathrm{0} \\ $$$${find}\:\:\frac{\mathrm{1}}{\boldsymbol{{log}}_{\boldsymbol{{a}}} \boldsymbol{{b}}}\:+\:\frac{\mathrm{1}}{\boldsymbol{{log}}_{\boldsymbol{{b}}} \boldsymbol{{c}}}\:+\:\frac{\mathrm{1}}{\boldsymbol{{log}}_{\boldsymbol{{c}}} \boldsymbol{{a}}}\:=\:? \\ $$

Question Number 145399 Answers: 1 Comments: 0

Prove that lim_(n→+∞) ∫^( n) _( 0) (t^n /(n!)) e^(−t) dt = (1/2)

$$\mathrm{Prove}\:\mathrm{that}\: \\ $$$$\underset{\boldsymbol{\mathrm{n}}\rightarrow+\infty} {\boldsymbol{\mathrm{lim}}}\:\:\underset{\:\mathrm{0}} {\int}^{\:\boldsymbol{\mathrm{n}}} \:\frac{\boldsymbol{\mathrm{t}}^{\boldsymbol{\mathrm{n}}} }{\boldsymbol{\mathrm{n}}!}\:\boldsymbol{{e}}^{−\boldsymbol{\mathrm{t}}} \:\boldsymbol{\mathrm{dt}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Question Number 145393 Answers: 2 Comments: 0

The number (2/(13)) expressed as a decimal is 0.153846153846... The 200th and 300th digits are?

$$\mathrm{The}\:\mathrm{number}\:\frac{\mathrm{2}}{\mathrm{13}}\:\mathrm{expressed}\:\mathrm{as}\:\mathrm{a}\:\mathrm{decimal}\:\mathrm{is}\:\mathrm{0}.\mathrm{153846153846}... \\ $$$$\mathrm{The}\:\mathrm{200th}\:\mathrm{and}\:\mathrm{300th}\:\mathrm{digits}\:\mathrm{are}? \\ $$

Question Number 145391 Answers: 2 Comments: 0

Developpement limite^ a l′ordre 2 de g(x)=((√(1+x^2 ))/(1+x+(√(1+x^2 ))))

$$\mathrm{Developpement}\:\mathrm{limit}\acute {\mathrm{e}}\:\mathrm{a}\:\mathrm{l}'\mathrm{ordre}\:\mathrm{2}\:\mathrm{de}\: \\ $$$$\mathrm{g}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{1}+\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }} \\ $$

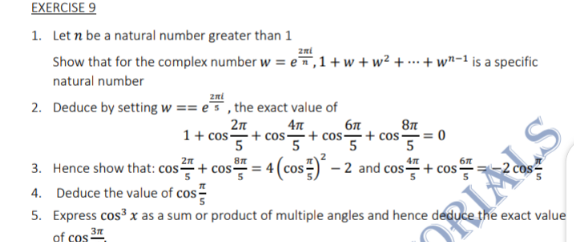
Question Number 145390 Answers: 1 Comments: 0

ϕ(x)=ln(((e^(x+cos(x)) −e)/(x+x^2 ))) montrer que ϕ se prolonge par continuite^ en 0. on note ψ son prolongement, montrer que ψ est de^ rivable en 0.. Ainsi donner une e^ quation de la tangente, position de la courbe par rapport a la tangente, et faire le dessin..

$$\varphi\left(\mathrm{x}\right)=\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}+\mathrm{cos}\left(\mathrm{x}\right)} −\mathrm{e}}{\mathrm{x}+\mathrm{x}^{\mathrm{2}} }\right) \\ $$$$\mathrm{montrer}\:\mathrm{que}\:\varphi\:\mathrm{se}\:\mathrm{prolonge}\:\mathrm{par}\:\mathrm{continuit}\acute {\mathrm{e}} \\ $$$$\mathrm{en}\:\mathrm{0}.\:\mathrm{on}\:\mathrm{note}\:\psi\:\mathrm{son}\:\mathrm{prolongement},\:\mathrm{montrer} \\ $$$$\mathrm{que}\:\psi\:\mathrm{est}\:\mathrm{d}\acute {\mathrm{e}rivable}\:\mathrm{en}\:\mathrm{0}..\:\:\mathrm{Ainsi}\:\mathrm{donner}\:\mathrm{une} \\ $$$$\acute {\mathrm{e}quation}\:\mathrm{de}\:\mathrm{la}\:\mathrm{tangente},\:\mathrm{position}\:\mathrm{de}\:\mathrm{la}\:\mathrm{courbe} \\ $$$$\mathrm{par}\:\mathrm{rapport}\:\mathrm{a}\:\mathrm{la}\:\mathrm{tangente},\:\mathrm{et}\:\mathrm{faire}\:\mathrm{le}\:\mathrm{dessin}.. \\ $$

Pg 718 Pg 719 Pg 720 Pg 721 Pg 722 Pg 723 Pg 724 Pg 725 Pg 726 Pg 727

Contact: info@tinkutara.com