Question and Answers Forum

AllQuestion and Answers: Page 722

Question Number 144190 Answers: 1 Comments: 0

Σ_(n=1) ^∞ ((5n)/(n^2 + 3)) = ?

$$\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{5}{n}}{{n}^{\mathrm{2}} \:+\:\mathrm{3}}\:=\:? \\ $$

Question Number 144186 Answers: 2 Comments: 0

Estimate ∫_0 ^(0.5) (√(1+x^4 )) dx with an error 0.0001

$${Estimate}\:\int_{\mathrm{0}} ^{\mathrm{0}.\mathrm{5}} \sqrt{\mathrm{1}+{x}^{\mathrm{4}} }\:{dx} \\ $$$${with}\:{an}\:{error}\:\mathrm{0}.\mathrm{0001} \\ $$

Question Number 144187 Answers: 1 Comments: 0

∫_0 ^(+∞) (u^2 /(u^8 +2u^4 +1))du

$$\int_{\mathrm{0}} ^{+\infty} \frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{8}} +\mathrm{2}{u}^{\mathrm{4}} +\mathrm{1}}{du} \\ $$

Question Number 144180 Answers: 2 Comments: 0

Prove that ∫^( +∞) _0 ((sh(𝛂t))/(sh(t)))dt = (𝛑/2)tan(((𝛑𝛂)/2))

$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\underset{\mathrm{0}} {\int}^{\:+\infty} \:\frac{\boldsymbol{\mathrm{sh}}\left(\boldsymbol{\alpha\mathrm{t}}\right)}{\boldsymbol{\mathrm{sh}}\left(\boldsymbol{\mathrm{t}}\right)}\boldsymbol{{dt}}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{2}}\boldsymbol{{tan}}\left(\frac{\boldsymbol{\pi\alpha}}{\mathrm{2}}\right) \\ $$

Question Number 144177 Answers: 1 Comments: 0

Question Number 144174 Answers: 1 Comments: 1

∫_0 ^π (sinx)^(2n) dx=....? ∀n∈N

$$\int_{\mathrm{0}} ^{\pi} \left({sinx}\right)^{\mathrm{2}{n}} {dx}=....?\:\:\:\forall{n}\in\mathbb{N} \\ $$

Question Number 144170 Answers: 2 Comments: 0

Question Number 144169 Answers: 1 Comments: 1

please find the value of sin ((2Π)/7)+sin ((4Π)/7)+sin ((8Π)/7)

$$\mathrm{please}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\mathrm{sin}\:\frac{\mathrm{2}\Pi}{\mathrm{7}}+\mathrm{sin}\:\frac{\mathrm{4}\Pi}{\mathrm{7}}+\mathrm{sin}\:\frac{\mathrm{8}\Pi}{\mathrm{7}} \\ $$

Question Number 144168 Answers: 1 Comments: 0

Question Number 144166 Answers: 1 Comments: 0

Given p^→ =(√2) i^ +2(√3) j^ + (√3) k^ & q^→ =a i^ +j^ +2k^ . If proj_q^→ p^→ = ((2(√2))/9) q^→ then ∣q^→ ∣ =?

$$\mathrm{Given}\:\overset{\rightarrow} {\mathrm{p}}=\sqrt{\mathrm{2}}\:\hat {\mathrm{i}}+\mathrm{2}\sqrt{\mathrm{3}}\:\hat {\mathrm{j}}+\:\sqrt{\mathrm{3}}\:\hat {\mathrm{k}}\:\&\: \\ $$$$\:\overset{\rightarrow} {\mathrm{q}}=\mathrm{a}\:\hat {\mathrm{i}}+\hat {\mathrm{j}}\:+\mathrm{2}\hat {\mathrm{k}}\:.\:\mathrm{If}\:\mathrm{proj}_{\overset{\rightarrow} {\mathrm{q}}} \:\overset{\rightarrow} {\mathrm{p}}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{9}}\:\overset{\rightarrow} {\mathrm{q}}\: \\ $$$$\mathrm{then}\:\mid\overset{\rightarrow} {\mathrm{q}}\mid\:=?\: \\ $$

Question Number 144164 Answers: 1 Comments: 0

In ΔABC given a=5, b=7 & c= 4. If ∡CAB = α then cot ((1/2)α)=?

$$\mathrm{In}\:\Delta\mathrm{ABC}\:\mathrm{given}\:\mathrm{a}=\mathrm{5},\:\mathrm{b}=\mathrm{7}\:\&\:\mathrm{c}=\:\mathrm{4}. \\ $$$$\mathrm{If}\:\measuredangle\mathrm{CAB}\:=\:\alpha\:\mathrm{then}\:\mathrm{cot}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\alpha\right)=? \\ $$

Question Number 144162 Answers: 0 Comments: 1

Question Number 144156 Answers: 1 Comments: 2

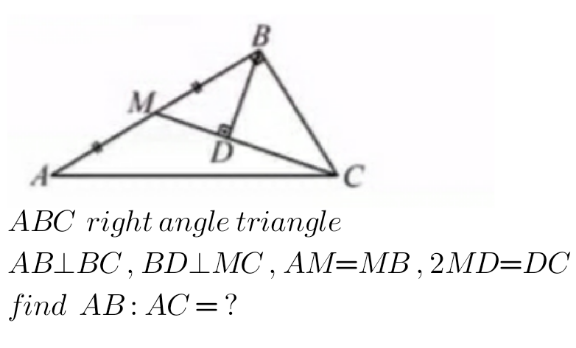
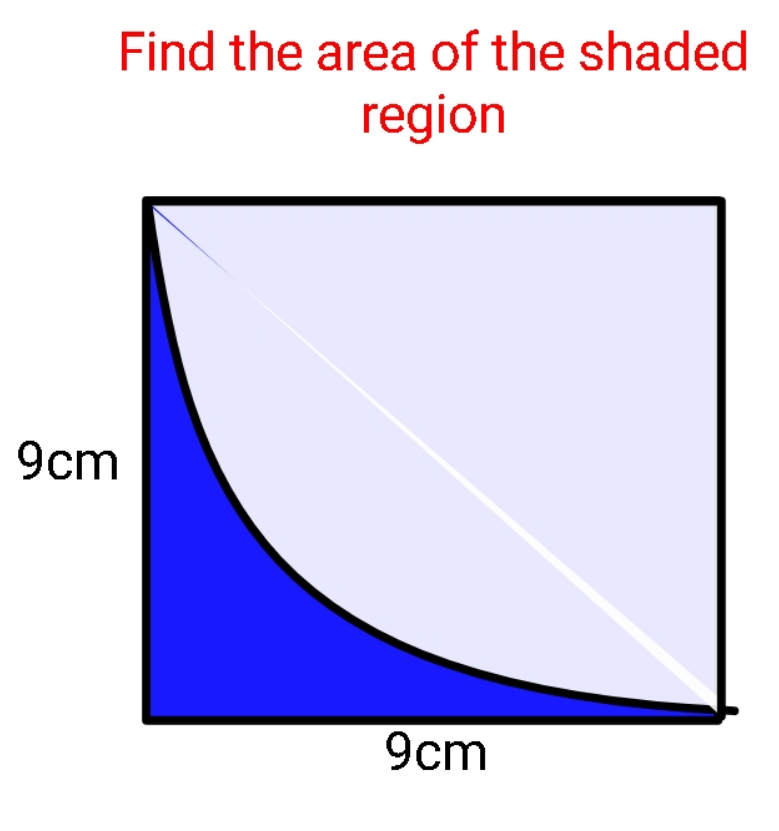
Question Number 144152 Answers: 2 Comments: 0

I=∫((e^x^2 +e^x )/(e^x^2 +1))dx=?

$$\mathrm{I}=\int\frac{\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } +\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{x}^{\mathrm{2}} } +\mathrm{1}}\mathrm{dx}=? \\ $$

Question Number 144148 Answers: 1 Comments: 0

{ ((2ln x+ln y = 2)),((x^2 + y = e^2 +1)) :}

$$\begin{cases}{\mathrm{2ln}\:\mathrm{x}+\mathrm{ln}\:\mathrm{y}\:=\:\mathrm{2}}\\{\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}\:=\:\mathrm{e}^{\mathrm{2}} +\mathrm{1}}\end{cases} \\ $$

Question Number 144143 Answers: 1 Comments: 0

∫_(1/a) ^a ((arctg(x))/x)dx=???

$$\int_{\frac{\mathrm{1}}{{a}}} ^{{a}} \frac{{arctg}\left({x}\right)}{{x}}{dx}=??? \\ $$

Question Number 144142 Answers: 1 Comments: 0

∫ ((√(cos x+(√(cos x+(√(cos x+(√(cos x+(√(...))))))))))/(sin x)) dx

$$\:\int\:\frac{\sqrt{\mathrm{cos}\:\mathrm{x}+\sqrt{\mathrm{cos}\:\mathrm{x}+\sqrt{\mathrm{cos}\:\mathrm{x}+\sqrt{\mathrm{cos}\:\mathrm{x}+\sqrt{...}}}}}}{\mathrm{sin}\:\mathrm{x}}\:\mathrm{dx} \\ $$

Question Number 144139 Answers: 2 Comments: 0

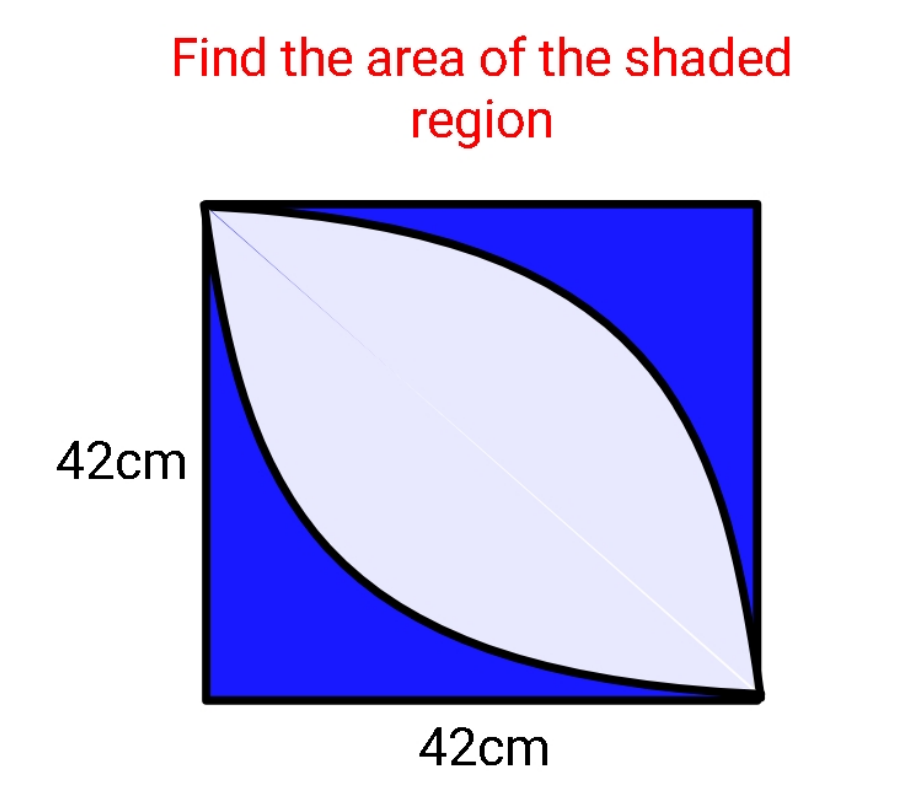
Question Number 144136 Answers: 0 Comments: 1

Question Number 144120 Answers: 2 Comments: 0

log_2 3 = x , log_3 5 = y , lg6 = ?

$${log}_{\mathrm{2}} \mathrm{3}\:=\:{x}\:,\:{log}_{\mathrm{3}} \mathrm{5}\:=\:{y}\:,\:{lg}\mathrm{6}\:=\:? \\ $$

Question Number 144118 Answers: 0 Comments: 0

Let a,b,c > 0 and a+b+c = 3. Prove that (((√(ab))+1)/( (√(ab))+(√c)))+(((√(bc))+1)/( (√(bc))+(√a)))+(((√(ca))+1)/( (√(ca))+(√b))) ≥ (√a)+(√b)+(√c)

$$\mathrm{Let}\:{a},{b},{c}\:>\:\mathrm{0}\:\mathrm{and}\:{a}+{b}+{c}\:=\:\mathrm{3}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\sqrt{{ab}}+\mathrm{1}}{\:\sqrt{{ab}}+\sqrt{{c}}}+\frac{\sqrt{{bc}}+\mathrm{1}}{\:\sqrt{{bc}}+\sqrt{{a}}}+\frac{\sqrt{{ca}}+\mathrm{1}}{\:\sqrt{{ca}}+\sqrt{{b}}}\:\geqslant\:\sqrt{{a}}+\sqrt{{b}}+\sqrt{{c}}\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Question Number 144116 Answers: 0 Comments: 0

Question Number 144109 Answers: 3 Comments: 1

hi, everybody ! 1. calculate : I =∫_(𝛑/6) ^( (𝛑/3)) ln(tan x)dx. 2. calculate : lim_(x → e) ((x(√(1−ln x)))/(x−e)) .

$$\boldsymbol{\mathrm{hi}},\:\boldsymbol{\mathrm{everybody}}\:! \\ $$$$\mathrm{1}.\:\boldsymbol{\mathrm{calculate}}\::\:\boldsymbol{\mathrm{I}}\:=\int_{\frac{\boldsymbol{\pi}}{\mathrm{6}}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{3}}} \boldsymbol{{ln}}\left(\boldsymbol{{tan}}\:\boldsymbol{{x}}\right)\boldsymbol{{dx}}. \\ $$$$\mathrm{2}.\:\boldsymbol{\mathrm{calculate}}\:\::\:\underset{\boldsymbol{{x}}\:\rightarrow\:\boldsymbol{{e}}} {\boldsymbol{{lim}}}\:\frac{\boldsymbol{{x}}\sqrt{\mathrm{1}−\boldsymbol{{ln}}\:\boldsymbol{{x}}}}{\boldsymbol{{x}}−\boldsymbol{{e}}}\:. \\ $$

Question Number 144107 Answers: 1 Comments: 0

A=lim_(n→+∝) ((1+(2)^(1/7) +(3)^(1/7) +(4)^(1/7) +.....+(n)^(1/7) )/( (n^9 )^(1/7) )) =?

$$\mathrm{A}=\underset{\mathrm{n}\rightarrow+\propto} {\mathrm{lim}}\frac{\mathrm{1}+\sqrt[{\mathrm{7}}]{\mathrm{2}}+\sqrt[{\mathrm{7}}]{\mathrm{3}}+\sqrt[{\mathrm{7}}]{\mathrm{4}}+.....+\sqrt[{\mathrm{7}}]{\mathrm{n}}}{\:\sqrt[{\mathrm{7}}]{\mathrm{n}^{\mathrm{9}} }}\:=? \\ $$

Question Number 144106 Answers: 1 Comments: 1

lim_(x→∞) ((4^(x-2) + 3^x + 2^x )/(4^(x-1) + 3^(x+1) )) = ?

$$\underset{{x}\rightarrow\infty} {{lim}}\frac{\mathrm{4}^{{x}-\mathrm{2}} \:+\:\mathrm{3}^{{x}} \:+\:\mathrm{2}^{{x}} }{\mathrm{4}^{{x}-\mathrm{1}} \:+\:\mathrm{3}^{{x}+\mathrm{1}} }\:=\:? \\ $$

Question Number 144095 Answers: 1 Comments: 0

if x>0 , r=pq , 1≤p≤q then: 1+rx ≤ (1+qx)^p ≤ (1+px)^q ≤ (1+x)^r

$${if}\:\:{x}>\mathrm{0}\:,\:{r}={pq}\:,\:\mathrm{1}\leqslant{p}\leqslant{q}\:\:{then}: \\ $$$$\mathrm{1}+{rx}\:\leqslant\:\left(\mathrm{1}+{qx}\right)^{\boldsymbol{{p}}} \:\leqslant\:\left(\mathrm{1}+{px}\right)^{\boldsymbol{{q}}} \:\leqslant\:\left(\mathrm{1}+{x}\right)^{\boldsymbol{{r}}} \\ $$

Pg 717 Pg 718 Pg 719 Pg 720 Pg 721 Pg 722 Pg 723 Pg 724 Pg 725 Pg 726

Contact: info@tinkutara.com