
AllQuestion and Answers: Page 720
Question Number 147466 Answers: 2 Comments: 0
Question Number 147465 Answers: 0 Comments: 0
Question Number 147459 Answers: 2 Comments: 0
Question Number 147453 Answers: 1 Comments: 2
Question Number 147444 Answers: 1 Comments: 0
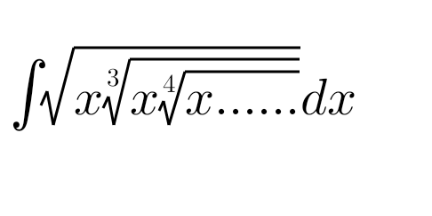
Question Number 147443 Answers: 0 Comments: 0

Question Number 147438 Answers: 0 Comments: 0

Question Number 147434 Answers: 0 Comments: 0
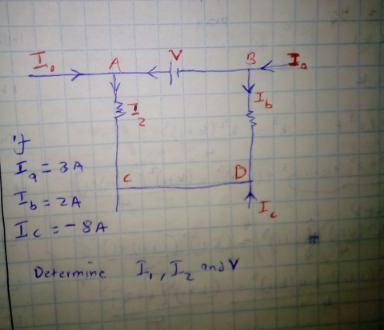
Question Number 147432 Answers: 1 Comments: 0
Question Number 147431 Answers: 2 Comments: 0

Question Number 147419 Answers: 1 Comments: 0
Question Number 147418 Answers: 1 Comments: 0
Question Number 147417 Answers: 1 Comments: 0
Question Number 147411 Answers: 2 Comments: 0

Question Number 147406 Answers: 1 Comments: 0
Question Number 147405 Answers: 1 Comments: 1
Question Number 147404 Answers: 1 Comments: 1
$${find}\:{taylor}\:{series}\:{of}\:{f}\left({z}\right)={cotz}\:,{z}=\mathrm{5}\pi \\ $$
Question Number 147402 Answers: 2 Comments: 0
Question Number 147399 Answers: 0 Comments: 0
Question Number 147397 Answers: 1 Comments: 0
Question Number 147396 Answers: 0 Comments: 0
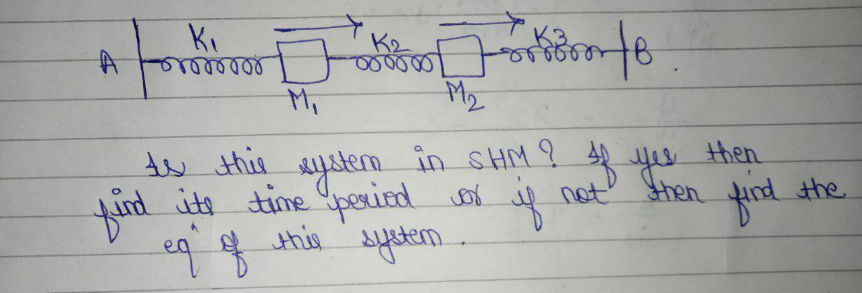
Question Number 147381 Answers: 1 Comments: 0
Question Number 147413 Answers: 0 Comments: 0
Question Number 147412 Answers: 1 Comments: 0
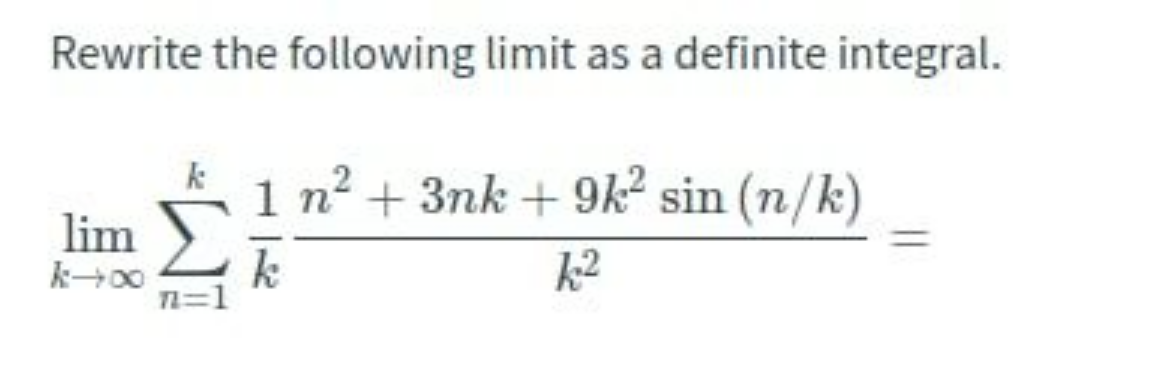
Question Number 147371 Answers: 1 Comments: 0
Question Number 147640 Answers: 1 Comments: 0
Pg 715 Pg 716 Pg 717 Pg 718 Pg 719 Pg 720 Pg 721 Pg 722 Pg 723 Pg 724
