
AllQuestion and Answers: Page 716
Question Number 147894 Answers: 2 Comments: 0
Question Number 147893 Answers: 0 Comments: 2
Question Number 147892 Answers: 1 Comments: 0
Question Number 147884 Answers: 0 Comments: 0
$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{−{x}} {x}^{{a}} {dx}\:\:{a}>\mathrm{0} \\ $$$$ \\ $$
Question Number 147882 Answers: 2 Comments: 0
Question Number 147879 Answers: 1 Comments: 0
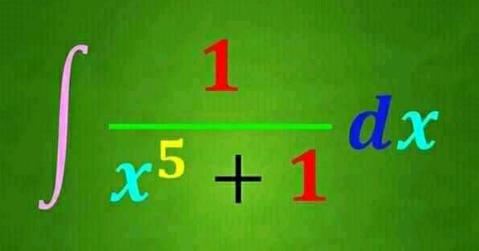
Question Number 147878 Answers: 1 Comments: 0
Question Number 147873 Answers: 1 Comments: 0
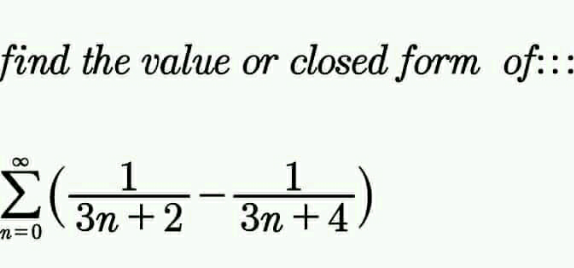
Question Number 147877 Answers: 1 Comments: 2
Question Number 147867 Answers: 3 Comments: 0
Question Number 147863 Answers: 1 Comments: 0
Question Number 147862 Answers: 1 Comments: 0
Question Number 147861 Answers: 0 Comments: 0
Question Number 147876 Answers: 1 Comments: 0

Question Number 147842 Answers: 0 Comments: 2
Question Number 147837 Answers: 1 Comments: 0
Question Number 147835 Answers: 0 Comments: 0
Question Number 147828 Answers: 1 Comments: 0
Question Number 147820 Answers: 1 Comments: 0
Question Number 147819 Answers: 1 Comments: 0
Question Number 147811 Answers: 1 Comments: 0
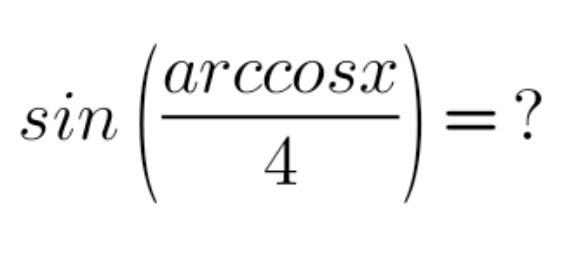
Question Number 147810 Answers: 1 Comments: 0
Question Number 147803 Answers: 0 Comments: 7
Question Number 147800 Answers: 1 Comments: 0
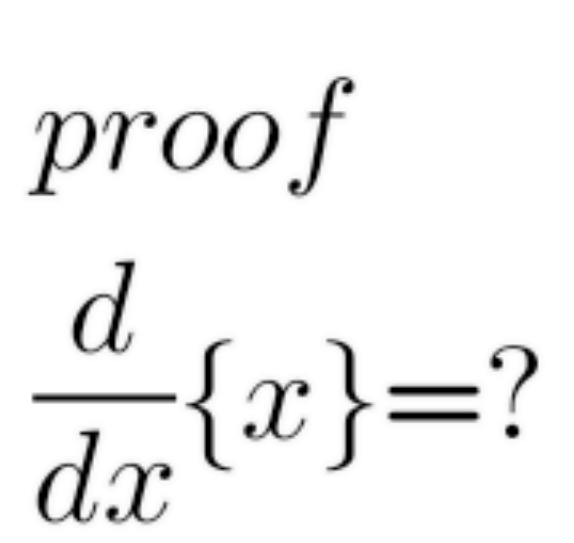
Question Number 147799 Answers: 1 Comments: 0
Question Number 147795 Answers: 1 Comments: 2
Pg 711 Pg 712 Pg 713 Pg 714 Pg 715 Pg 716 Pg 717 Pg 718 Pg 719 Pg 720
