Question and Answers Forum

AllQuestion and Answers: Page 713

Question Number 144828 Answers: 2 Comments: 0

2sin 17x+(√3) cos 5x+sin 5x=0 x=?

$$\mathrm{2sin}\:\mathrm{17}{x}+\sqrt{\mathrm{3}}\:\mathrm{cos}\:\mathrm{5}{x}+\mathrm{sin}\:\mathrm{5}{x}=\mathrm{0} \\ $$$${x}=? \\ $$

Question Number 144826 Answers: 1 Comments: 0

Question Number 144825 Answers: 1 Comments: 0

Σ_(k=0) ^∞ (k/(k^4 + 4)) = ?

$$\underset{\boldsymbol{{k}}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{{k}}{{k}^{\mathrm{4}} \:+\:\mathrm{4}}\:=\:? \\ $$

Question Number 144823 Answers: 1 Comments: 0

Let a,b > 0 and a+b+1 = 3ab. Prove that ((a+1)/(b+1))+((b+1)/(a+1)) ≤ a+b

$$\mathrm{Let}\:{a},{b}\:>\:\mathrm{0}\:\mathrm{and}\:{a}+{b}+\mathrm{1}\:=\:\mathrm{3}{ab}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{a}+\mathrm{1}}{{b}+\mathrm{1}}+\frac{{b}+\mathrm{1}}{{a}+\mathrm{1}}\:\leqslant\:{a}+{b} \\ $$

Question Number 144822 Answers: 1 Comments: 0

sin^3 xcos x−cos^3 xsin x=(1/4) x=?

$$\mathrm{sin}\:^{\mathrm{3}} {x}\mathrm{cos}\:{x}−\mathrm{cos}\:^{\mathrm{3}} {x}\mathrm{sin}\:{x}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${x}=? \\ $$

Question Number 144821 Answers: 0 Comments: 1

tan 193=k cos 167=?

$$\mathrm{tan}\:\mathrm{193}={k} \\ $$$$\mathrm{cos}\:\mathrm{167}=? \\ $$

Question Number 144820 Answers: 1 Comments: 0

Question Number 144816 Answers: 2 Comments: 0

lim_(x→0) (((√(1+6x^2 ))−(1+7x))/(x^2 (x−3))) =?

$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}+\mathrm{6x}^{\mathrm{2}} }−\left(\mathrm{1}+\mathrm{7x}\right)}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}−\mathrm{3}\right)}\:=? \\ $$

Question Number 144815 Answers: 1 Comments: 0

Question Number 144811 Answers: 0 Comments: 0

∫{(3/( (√(x^2 −tan^2 x))))}dx

$$\int\left\{\frac{\mathrm{3}}{\:\sqrt{{x}^{\mathrm{2}} −{tan}^{\mathrm{2}} {x}}}\right\}{dx} \\ $$

Question Number 144810 Answers: 0 Comments: 0

Question Number 144801 Answers: 1 Comments: 2

if you know that the probability of a picture appearing when acoin is tossed is 2/5 then the probability of getting writings when this coin is tossed 6 times ?

$${if}\:{you}\:{know}\:{that}\:{the}\:{probability}\:{of}\:{a}\:{picture} \\ $$$${appearing}\:{when}\:{acoin}\:{is}\:{tossed}\:{is}\:\mathrm{2}/\mathrm{5} \\ $$$${then}\:{the}\:{probability}\:{of}\:{getting}\:{writings}\: \\ $$$${when}\:{this}\:{coin}\:{is}\:{tossed}\:\mathrm{6}\:{times}\:? \\ $$

Question Number 144800 Answers: 1 Comments: 0

Let β be an acute angle such that the equation x^2 +4xcos β+cot β=0 involving variable x has multiple roots. Then the measure of β in radians is __

$$\mathrm{Let}\:\beta\:\mathrm{be}\:\mathrm{an}\:\mathrm{acute}\:\mathrm{angle}\:\mathrm{such} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{x}^{\mathrm{2}} +\mathrm{4xcos}\:\beta+\mathrm{cot}\:\beta=\mathrm{0} \\ $$$$\mathrm{involving}\:\mathrm{variable}\:\mathrm{x}\:\mathrm{has}\:\mathrm{multiple} \\ $$$$\mathrm{roots}.\:\mathrm{Then}\:\mathrm{the}\:\mathrm{measure}\:\mathrm{of}\:\beta\:\mathrm{in} \\ $$$$\mathrm{radians}\:\mathrm{is}\:\_\_ \\ $$

Question Number 144799 Answers: 0 Comments: 0

Question Number 144794 Answers: 0 Comments: 0

Question Number 144792 Answers: 1 Comments: 0

∫ ((2x^3 −1)/(x^4 +x)) dx ?

$$\:\int\:\frac{\mathrm{2x}^{\mathrm{3}} −\mathrm{1}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}}\:\mathrm{dx}\:? \\ $$

Question Number 144791 Answers: 1 Comments: 0

Express sin 5x as polynomial in terms of sin x.

$$\:\mathrm{Express}\:\mathrm{sin}\:\mathrm{5x}\:\mathrm{as}\:\mathrm{polynomial} \\ $$$$\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{sin}\:\mathrm{x}.\: \\ $$

Question Number 144813 Answers: 0 Comments: 1

I:=∫_0 ^( 1) ((ln (x))/(1 + x^( 2) )) dx := ∫_0 ^( 1) ln(x ) Σ_(n=0) ^∞ (−1)^( n) x^( 2n) dx := Σ_(n=0) ^∞ ( −1 )^( n) ∫_0 ^( 1) x^( 2n) ln( x )dx : = Σ_(n=0) ^∞ ( −1 )^( n) { [(x^( 2n+1) /(2n +1)) ln ( x )]_0 ^( 1) −(1/((2n +1 )^( 2) )) } : = Σ_(n=1) ^( ∞) ((( −1 )^( n−1) )/(( 2n +1)^( 2) )) = −G (Catalan constant )

$$ \\ $$$$\:\:\:\:\:\:\mathrm{I}:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\:\left({x}\right)}{\mathrm{1}\:+\:{x}^{\:\mathrm{2}} }\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\::=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{ln}\left({x}\:\right)\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\:{n}} \:{x}^{\:\mathrm{2}{n}} \:{dx} \\ $$$$\:\:\:\:\:\:\:\::=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\left(\:−\mathrm{1}\:\right)^{\:{n}} \:\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\:\mathrm{2}{n}} \:\mathrm{ln}\left(\:{x}\:\right){dx} \\ $$$$\:\:\:\:\:\:\:\::\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\:−\mathrm{1}\:\right)^{\:{n}} \left\{\:\left[\frac{{x}^{\:\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}\:+\mathrm{1}}\:\mathrm{ln}\:\left(\:{x}\:\right)\right]_{\mathrm{0}} ^{\:\mathrm{1}} −\frac{\mathrm{1}}{\left(\mathrm{2}{n}\:+\mathrm{1}\:\right)^{\:\mathrm{2}} \:}\:\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\::\:=\:\underset{{n}=\mathrm{1}} {\overset{\:\infty} {\sum}}\frac{\left(\:−\mathrm{1}\:\right)^{\:{n}−\mathrm{1}} }{\left(\:\mathrm{2}{n}\:+\mathrm{1}\right)^{\:\mathrm{2}} }\:=\:−\mathrm{G}\:\:\left(\mathrm{Catalan}\:\mathrm{constant}\:\right) \\ $$

Question Number 144789 Answers: 0 Comments: 0

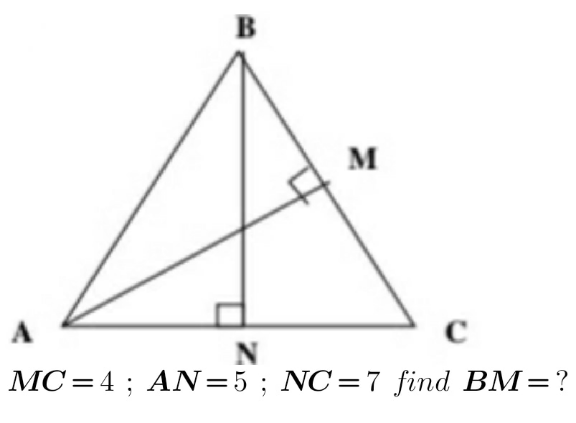
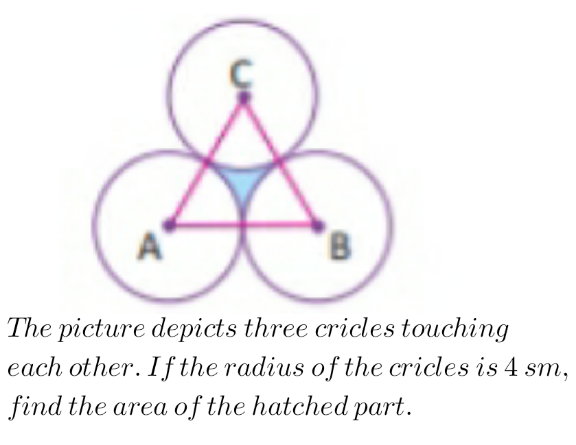
Question Number 144788 Answers: 1 Comments: 0

Question Number 144787 Answers: 1 Comments: 0

Q :: # Calculus # If : 𝛗 ( n ) : = ∫_0 ^( 1) (( x^( 2n) )/(1 + x^( 2) )) dx then find the value of :: S := Σ_(n=1) ^∞ ((( −1 )^( n) 𝛗 ( n ))/n) = ? m.n.july.1970

Question Number 144785 Answers: 0 Comments: 0

Question Number 144783 Answers: 0 Comments: 1

Question Number 144782 Answers: 0 Comments: 0

Question Number 144781 Answers: 1 Comments: 0

Question Number 144780 Answers: 0 Comments: 0

Let x∈[−((5π)/(12)),−(π/3)] , then the maximum value of y=tan (x+((2π)/3))−tan (x+(π/6))+cos (x+(π/6)) is

$$\:\mathrm{Let}\:\mathrm{x}\in\left[−\frac{\mathrm{5}\pi}{\mathrm{12}},−\frac{\pi}{\mathrm{3}}\right]\:,\:\mathrm{then}\:\mathrm{the}\: \\ $$$$\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of}\: \\ $$$$\:\:\mathrm{y}=\mathrm{tan}\:\left(\mathrm{x}+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)−\mathrm{tan}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{6}}\right)+\mathrm{cos}\:\left(\mathrm{x}+\frac{\pi}{\mathrm{6}}\right) \\ $$$$\:\mathrm{is}\: \\ $$

Pg 708 Pg 709 Pg 710 Pg 711 Pg 712 Pg 713 Pg 714 Pg 715 Pg 716 Pg 717

Contact: info@tinkutara.com