Question and Answers Forum

AllQuestion and Answers: Page 711

Question Number 141574 Answers: 0 Comments: 0

Question Number 141570 Answers: 1 Comments: 0

Question Number 141560 Answers: 1 Comments: 0

........Nice ....Calculus(I)...... Evaluate:: I:=∫_0 ^( ln(2)) (x/(e^x +2e^(−x) −2))dx=? ......

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:........{Nice}\:....{Calculus}\left({I}\right)...... \\ $$$$\:\:\:\:\:{Evaluate}::\:\: \\ $$$$\:\:\:\:\:\mathrm{I}:=\int_{\mathrm{0}} ^{\:{ln}\left(\mathrm{2}\right)} \frac{{x}}{{e}^{{x}} +\mathrm{2}{e}^{−{x}} −\mathrm{2}}{dx}=? \\ $$$$\:\:\:\:...... \\ $$

Question Number 141551 Answers: 0 Comments: 3

Question Number 141568 Answers: 0 Comments: 2

Question Number 141535 Answers: 0 Comments: 1

how can solve this with by steps please ((Γ((3/2))Γ((7/2)))/(2Γ(5))) i want solution step by step because i understand this?

$${how}\:{can}\:{solve}\:{this}\:{with}\:{by}\:{steps}\:{please} \\ $$$$\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{7}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\mathrm{5}\right)}\:{i}\:{want}\:{solution}\:{step}\:{by}\:{step} \\ $$$${because}\:{i}\:{understand}\:{this}? \\ $$$$ \\ $$

Question Number 141534 Answers: 1 Comments: 0

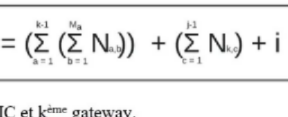
Question Number 141533 Answers: 1 Comments: 0

Question Number 141532 Answers: 1 Comments: 0

Question Number 141531 Answers: 0 Comments: 1

Question Number 141530 Answers: 0 Comments: 1

Question Number 141529 Answers: 0 Comments: 0

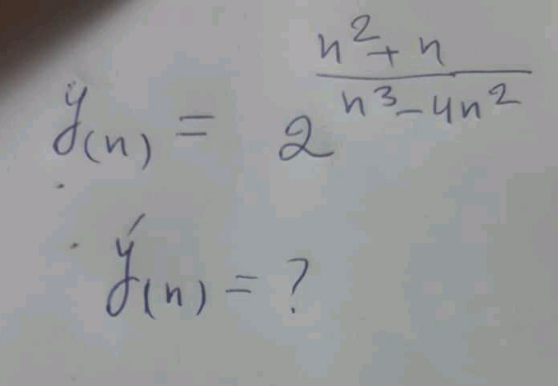
Question Number 141528 Answers: 0 Comments: 0

Question Number 141526 Answers: 1 Comments: 0

Question Number 141525 Answers: 1 Comments: 0

Let <x_n > be a sequence defined by x_(n+1) = (1/k)(x_n +(k/x_n )) ∀ n ∈ N Show that <x_n > converges to (√(k/(k−1))) x_1 >0 , k>1

$$\mathrm{Let}\:<\mathrm{x}_{\mathrm{n}} >\:\mathrm{be}\:\mathrm{a}\:\mathrm{sequence}\:\mathrm{defined}\:\mathrm{by} \\ $$$$\mathrm{x}_{\mathrm{n}+\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{k}}\left(\mathrm{x}_{\mathrm{n}} +\frac{\mathrm{k}}{\mathrm{x}_{\mathrm{n}} }\right)\:\forall\:\mathrm{n}\:\in\:\mathbb{N} \\ $$$$\mathrm{Show}\:\mathrm{that}\:<\mathrm{x}_{\mathrm{n}} >\:\mathrm{converges}\:\mathrm{to}\:\sqrt{\frac{\mathrm{k}}{\mathrm{k}−\mathrm{1}}} \\ $$$$\mathrm{x}_{\mathrm{1}} >\mathrm{0}\:,\:\mathrm{k}>\mathrm{1} \\ $$

Question Number 141521 Answers: 1 Comments: 0

{ ((((x+y))^(1/3) +(√(x−3y))=4)),((2x+3y=17)) :} Find x and y.

$$\begin{cases}{\sqrt[{\mathrm{3}}]{\boldsymbol{{x}}+\boldsymbol{{y}}}+\sqrt{\boldsymbol{{x}}−\mathrm{3}\boldsymbol{{y}}}=\mathrm{4}}\\{\mathrm{2}\boldsymbol{{x}}+\mathrm{3}\boldsymbol{{y}}=\mathrm{17}}\end{cases} \\ $$$$\boldsymbol{\mathrm{Find}}\:\boldsymbol{\mathrm{x}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{y}}. \\ $$

Question Number 141513 Answers: 0 Comments: 0

1. 27^((1/(log_2 3)) + log_(125) 0,2) =? 2. if, α = (π/(12)) find, cos^2 α + 2sinαcosα − sin^2 α=?

$$\mathrm{1}.\:\:\mathrm{27}^{\frac{\mathrm{1}}{{log}_{\mathrm{2}} \mathrm{3}}\:+\:{log}_{\mathrm{125}} \mathrm{0},\mathrm{2}} =? \\ $$$$\mathrm{2}.\:\:{if},\:\:\alpha\:=\:\frac{\pi}{\mathrm{12}} \\ $$$${find},\:\:{cos}^{\mathrm{2}} \alpha\:+\:\mathrm{2}{sin}\alpha{cos}\alpha\:−\:{sin}^{\mathrm{2}} \alpha=? \\ $$

Question Number 141512 Answers: 0 Comments: 0

Σ_(n=1 ) ^∞ ((sin((((2n−1)π)/6)))/((2n−1)^2 )) = a.G a = ? (G:= catalan constant)

$$ \\ $$$$\:\:\:\underset{{n}=\mathrm{1}\:} {\overset{\infty} {\sum}}\frac{{sin}\left(\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)\pi}{\mathrm{6}}\right)}{\left(\mathrm{2}{n}−\mathrm{1}\right)^{\mathrm{2}} }\:=\:{a}.{G} \\ $$$$\:\:{a}\:=\:?\:\:\:\:\:\:\left({G}:=\:{catalan}\:{constant}\right) \\ $$$$ \\ $$

Question Number 141509 Answers: 1 Comments: 0

lim_(θ→0) ((sin^3 3θ − 3θ^3 )/(θ^3 + θ^4 ))

$$\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}\:\:\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{3}\theta\:\:\:−\:\:\:\mathrm{3}\theta^{\mathrm{3}} }{\theta^{\mathrm{3}} \:\:+\:\:\theta^{\mathrm{4}} } \\ $$

Question Number 141507 Answers: 3 Comments: 0

∫ (dx/(sin^4 x + cos^4 x)) dx

$$\int\:\frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{4}} \mathrm{x}\:\:\:+\:\:\:\mathrm{cos}^{\mathrm{4}} \mathrm{x}}\:\:\mathrm{dx} \\ $$

Question Number 141501 Answers: 0 Comments: 0

Question Number 141499 Answers: 0 Comments: 0

Question Number 141496 Answers: 3 Comments: 0

∫((√(2+9x^2 ))/x)dx SOS SOS HELP

$$\int\frac{\sqrt{\mathrm{2}+\mathrm{9}{x}^{\mathrm{2}} }}{{x}}{dx} \\ $$$${SOS}\:{SOS}\:{HELP} \\ $$

Question Number 141494 Answers: 0 Comments: 0

(((0 −1)),((0 0)) )!= (((1 γ)),((0 1)) ) γ=Euler Mascheroni Constant What is the physical representation of a Matrix factorial?

$$\begin{pmatrix}{\mathrm{0}\:−\mathrm{1}}\\{\mathrm{0}\:\:\:\mathrm{0}}\end{pmatrix}!=\begin{pmatrix}{\mathrm{1}\:\:\gamma}\\{\mathrm{0}\:\:\mathrm{1}}\end{pmatrix}\:\:\:\:\:\:\gamma=\boldsymbol{{E}}{uler}\:{Mascheroni}\:{Constant} \\ $$$${What}\:{is}\:{the}\:{physical}\:{representation}\:{of}\:{a}\:{Matrix}\:{factorial}? \\ $$

Question Number 141475 Answers: 2 Comments: 0

Find the smallest value of (√(x^2 +y^2 )) among all values of x & y satisfying 3x−y = 20

$$\:{Find}\:{the}\:{smallest}\:{value}\:{of}\: \\ $$$$\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:{among}\:{all}\:{values}\:{of} \\ $$$$\:{x}\:\&\:{y}\:{satisfying}\:\mathrm{3}{x}−{y}\:=\:\mathrm{20}\: \\ $$

Question Number 141469 Answers: 3 Comments: 0

simplify (log_3 11)(log_(11) 13)(log_(13) 15)(log_(15) 27)(log_(27) 81) please i need help

$$\mathrm{simplify} \\ $$$$\left(\mathrm{log}_{\mathrm{3}} \mathrm{11}\right)\left(\mathrm{log}_{\mathrm{11}} \mathrm{13}\right)\left(\mathrm{log}_{\mathrm{13}} \mathrm{15}\right)\left(\mathrm{log}_{\mathrm{15}} \mathrm{27}\right)\left(\mathrm{log}_{\mathrm{27}} \mathrm{81}\right) \\ $$$$\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{help} \\ $$

Pg 706 Pg 707 Pg 708 Pg 709 Pg 710 Pg 711 Pg 712 Pg 713 Pg 714 Pg 715

Contact: info@tinkutara.com