
AllQuestion and Answers: Page 700
Question Number 149481 Answers: 1 Comments: 0

Question Number 149478 Answers: 2 Comments: 2
Question Number 149474 Answers: 0 Comments: 2
Question Number 149471 Answers: 1 Comments: 0
Question Number 149468 Answers: 1 Comments: 0
Question Number 149467 Answers: 1 Comments: 0
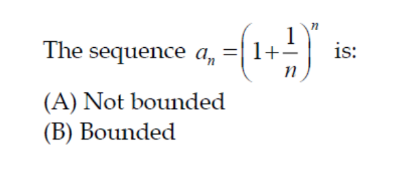
Question Number 149462 Answers: 1 Comments: 0

Question Number 149469 Answers: 1 Comments: 0
Question Number 149463 Answers: 1 Comments: 0
Question Number 149458 Answers: 1 Comments: 3

Question Number 149457 Answers: 1 Comments: 0
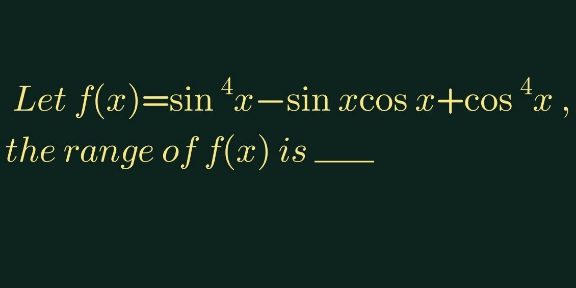
Question Number 149454 Answers: 0 Comments: 0

Question Number 149424 Answers: 1 Comments: 0
Question Number 149423 Answers: 1 Comments: 0
Question Number 149415 Answers: 1 Comments: 1
Question Number 149410 Answers: 1 Comments: 0
Question Number 149408 Answers: 0 Comments: 2
Question Number 149406 Answers: 0 Comments: 0
Question Number 149405 Answers: 0 Comments: 2
Question Number 149400 Answers: 3 Comments: 0
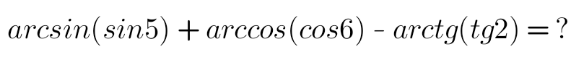
Question Number 149395 Answers: 1 Comments: 0

Question Number 149385 Answers: 4 Comments: 0

Question Number 149383 Answers: 1 Comments: 1

Question Number 149378 Answers: 3 Comments: 0
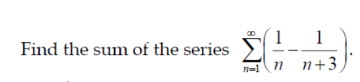
Question Number 149377 Answers: 1 Comments: 0

Question Number 149372 Answers: 1 Comments: 0

Pg 695 Pg 696 Pg 697 Pg 698 Pg 699 Pg 700 Pg 701 Pg 702 Pg 703 Pg 704
