
AllQuestion and Answers: Page 698
Question Number 150095 Answers: 1 Comments: 0
$$\Omega\:=\int\:\frac{\mathrm{x}\:\mathrm{dx}}{\mathrm{x}^{\mathrm{8}} \:-\:\mathrm{1}}\:=\:? \\ $$
Question Number 149770 Answers: 0 Comments: 2
Question Number 149768 Answers: 0 Comments: 0

Question Number 149766 Answers: 1 Comments: 2
Question Number 149757 Answers: 0 Comments: 1

Question Number 149739 Answers: 3 Comments: 0
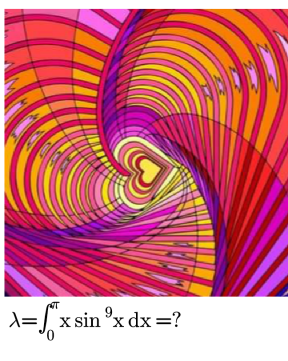
Question Number 149731 Answers: 0 Comments: 2
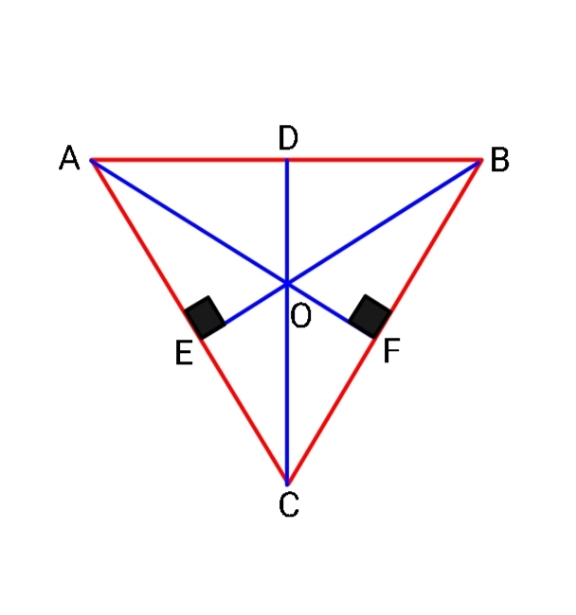
Question Number 149733 Answers: 1 Comments: 0

Question Number 149720 Answers: 1 Comments: 0

Question Number 149718 Answers: 1 Comments: 0
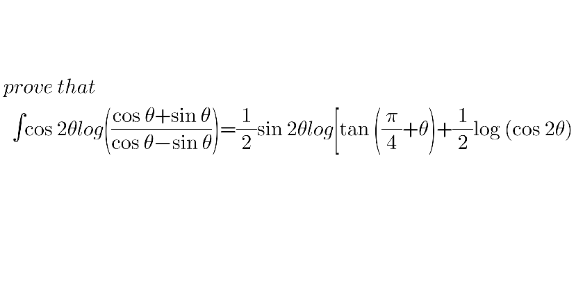
Question Number 149686 Answers: 2 Comments: 2

Question Number 149675 Answers: 0 Comments: 0
Question Number 149673 Answers: 3 Comments: 0
Question Number 149670 Answers: 1 Comments: 0
Question Number 149667 Answers: 2 Comments: 0
Question Number 149660 Answers: 1 Comments: 0
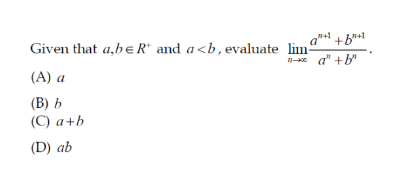
Question Number 150362 Answers: 1 Comments: 0
Question Number 149638 Answers: 0 Comments: 0
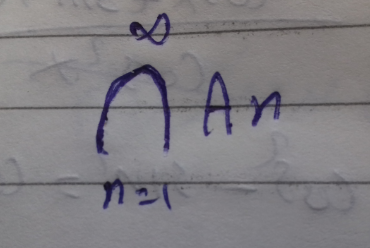
Question Number 149637 Answers: 2 Comments: 0

Question Number 149636 Answers: 1 Comments: 0

Question Number 149634 Answers: 1 Comments: 0
Question Number 152856 Answers: 0 Comments: 2
Question Number 152601 Answers: 2 Comments: 1
Question Number 149628 Answers: 1 Comments: 0
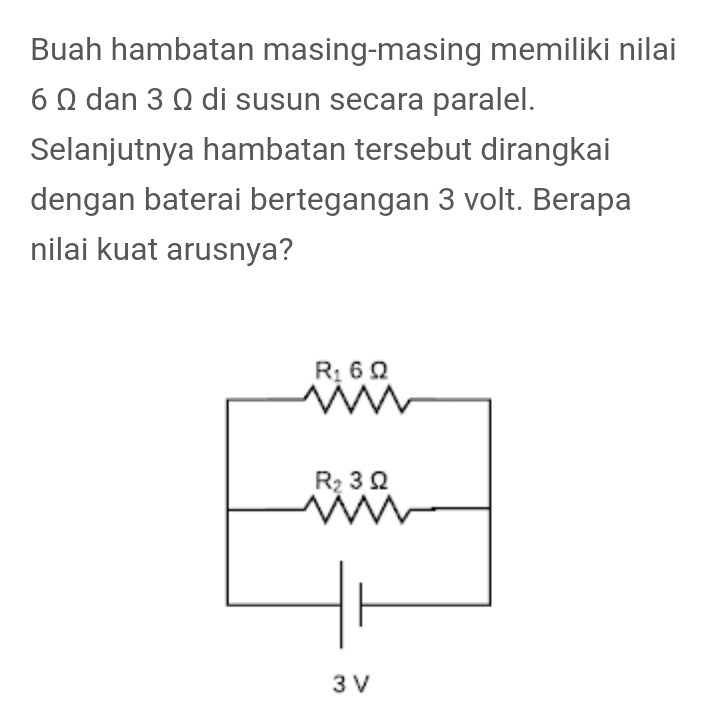
Question Number 149625 Answers: 1 Comments: 0
Question Number 149623 Answers: 1 Comments: 0
Pg 693 Pg 694 Pg 695 Pg 696 Pg 697 Pg 698 Pg 699 Pg 700 Pg 701 Pg 702
