Question and Answers Forum

AllQuestion and Answers: Page 696

Question Number 149914 Answers: 0 Comments: 0

show that∫_1 ^2 (((2+6θ^2 −2𝛉^3 )/(𝛉^2 (𝛉^2 +1))))d𝛉=1.606

$$\boldsymbol{{show}}\:\boldsymbol{{that}}\int_{\mathrm{1}} ^{\mathrm{2}} \left(\frac{\mathrm{2}+\mathrm{6}\theta^{\mathrm{2}} −\mathrm{2}\boldsymbol{\theta}^{\mathrm{3}} }{\boldsymbol{\theta}^{\mathrm{2}} \left(\boldsymbol{\theta}^{\mathrm{2}} +\mathrm{1}\right)}\right)\boldsymbol{{d}\theta}=\mathrm{1}.\mathrm{606} \\ $$

Question Number 149903 Answers: 1 Comments: 0

Ω = ∫_0 ^(π/2) ((cos^3 x)/( (√(1−cos^2 x)))) dx

$$\:\Omega\:=\:\underset{\mathrm{0}} {\overset{\frac{\pi}{\mathrm{2}}} {\int}}\:\frac{\mathrm{cos}\:^{\mathrm{3}} \mathrm{x}}{\:\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}}\:\mathrm{dx}\: \\ $$

Question Number 149894 Answers: 1 Comments: 1

Question Number 149891 Answers: 1 Comments: 0

if x;y;z;m;n;p∈R^+ then prove that: Σ_(cyc) ((m(x+y))/( (√((n+2p)x^2 +2nxy+(n+2p)y^2 )))) ≤ ((3m)/( (√(n+p))))

$$\mathrm{if}\:\:\:\mathrm{x};\mathrm{y};\mathrm{z};\mathrm{m};\mathrm{n};\mathrm{p}\in\mathbb{R}^{+} \:\mathrm{then}\:\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\underset{\boldsymbol{\mathrm{cyc}}} {\sum}\:\frac{\mathrm{m}\left(\mathrm{x}+\mathrm{y}\right)}{\:\sqrt{\left(\mathrm{n}+\mathrm{2p}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{2nxy}+\left(\mathrm{n}+\mathrm{2p}\right)\mathrm{y}^{\mathrm{2}} }}\:\leqslant\:\frac{\mathrm{3m}}{\:\sqrt{\mathrm{n}+\mathrm{p}}} \\ $$

Question Number 149889 Answers: 0 Comments: 3

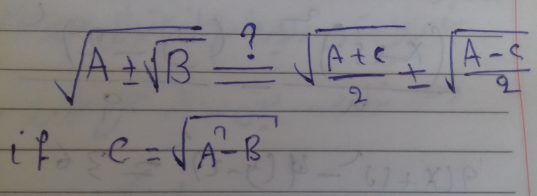
Question Number 149886 Answers: 0 Comments: 0

lim_(x→0^+ ) ((ln^2 (x))/x^2 )(((ln (sin ((x/2))))/(ln (sin (x)))) +((ln 2)/(ln (x)))) =?

$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{ln}\:^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }\left(\frac{\mathrm{ln}\:\left(\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)}{\mathrm{ln}\:\left(\mathrm{sin}\:\left(\mathrm{x}\right)\right)}\:+\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{ln}\:\left(\mathrm{x}\right)}\right)\:=? \\ $$

Question Number 149885 Answers: 1 Comments: 0

I_n =∫_0 ^(π/4) (dx/(cos^(2n+1) x)) to show that : ∀ n∈N^∗ , 2nI_n =(2n−1)I_(n−1) +(2^n /( (√2))) (I_n =∫_0 ^(π/4) ((1/(cos^(2n−1) x))×(1/(cos^2 x)))dx)...

$${I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{dx}}{{cos}^{\mathrm{2}{n}+\mathrm{1}} {x}} \\ $$$${to}\:{show}\:{that}\:: \\ $$$$\forall\:{n}\in\mathbb{N}^{\ast} ,\:\mathrm{2}{nI}_{{n}} =\left(\mathrm{2}{n}−\mathrm{1}\right){I}_{{n}−\mathrm{1}} +\frac{\mathrm{2}^{{n}} }{\:\sqrt{\mathrm{2}}} \\ $$$$\left({I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}{n}−\mathrm{1}} {x}}×\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}\right){dx}\right)... \\ $$

Question Number 149883 Answers: 1 Comments: 0

Prove that ((2+(√5)))^(1/3) +((2−(√5)))^(1/3) is a rational number

$$\mathrm{Prove}\:\mathrm{that}\:\sqrt[{\mathrm{3}}]{\mathrm{2}+\sqrt{\mathrm{5}}}+\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt{\mathrm{5}}}\:\mathrm{is} \\ $$$$\mathrm{a}\:\mathrm{rational}\:\mathrm{number} \\ $$

Question Number 149876 Answers: 2 Comments: 0

Question Number 149871 Answers: 1 Comments: 0

lim_(x→2) ((3^(x!) −9)/(x−2))

$${lim}_{{x}\rightarrow\mathrm{2}} \frac{\mathrm{3}^{{x}!} −\mathrm{9}}{{x}−\mathrm{2}} \\ $$

Question Number 149870 Answers: 0 Comments: 3

if x;y;z;m;n∈R^+ then: Σ_(cyc) (b^(−1) /((m(√x) + n(√y))^2 )) ≥ (3/((m + n)^2 ))

$$\mathrm{if}\:\:\:\mathrm{x};\mathrm{y};\mathrm{z};\mathrm{m};\mathrm{n}\in\mathbb{R}^{+} \:\:\mathrm{then}: \\ $$$$\underset{\boldsymbol{\mathrm{cyc}}} {\sum}\:\frac{\mathrm{b}^{−\mathrm{1}} }{\left(\mathrm{m}\sqrt{\mathrm{x}}\:+\:\mathrm{n}\sqrt{\mathrm{y}}\right)^{\mathrm{2}} }\:\geqslant\:\frac{\mathrm{3}}{\left(\mathrm{m}\:+\:\mathrm{n}\right)^{\mathrm{2}} } \\ $$

Question Number 149852 Answers: 0 Comments: 0

What angle is subtended at the centre of the Earth by an arc of the equator of length 1) 2002km 2) 30030km

Question Number 149868 Answers: 1 Comments: 0

if a;b and c are the dimensions of a cuboid with the diagonal d then prove d ≤ (√((a^3 /b) + (b^3 /c) + (c^3 /a)))

$$\mathrm{if}\:\:\mathrm{a};\mathrm{b}\:\:\mathrm{and}\:\:\mathrm{c}\:\:\mathrm{are}\:\mathrm{the}\:\mathrm{dimensions}\:\mathrm{of}\:\:\mathrm{a} \\ $$$$\mathrm{cuboid}\:\mathrm{with}\:\mathrm{the}\:\mathrm{diagonal}\:\boldsymbol{\mathrm{d}}\:\mathrm{then}\:\mathrm{prove} \\ $$$$\mathrm{d}\:\leqslant\:\sqrt{\frac{\mathrm{a}^{\mathrm{3}} }{\mathrm{b}}\:+\:\frac{\mathrm{b}^{\mathrm{3}} }{\mathrm{c}}\:+\:\frac{\mathrm{c}^{\mathrm{3}} }{\mathrm{a}}} \\ $$

Question Number 150356 Answers: 3 Comments: 0

solve... I:= ∫_0 ^( 1) (( Arcsin ((√x) ))/(1−x + x^( 2) )) dx=?

$$\:{solve}... \\ $$$$\:\:\:\:\:\mathrm{I}:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\mathrm{Arcsin}\:\left(\sqrt{{x}}\:\right)}{\mathrm{1}−{x}\:+\:{x}^{\:\mathrm{2}} }\:{dx}=? \\ $$

Question Number 149865 Answers: 1 Comments: 0

Question Number 149830 Answers: 1 Comments: 0

lim_(x→0) ((√(x−(√(x−(√(x−...))))))/(sin (sin (sin (....x)))=?

$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\sqrt{{x}−\sqrt{{x}−\sqrt{{x}−...}}}}{{sin}\:\left({sin}\:\left({sin}\:\left(....{x}\right)\right.\right.}=? \\ $$

Question Number 149955 Answers: 1 Comments: 0

If a group consist of 8 men and 6 women, in how many ways can a committee of 5 be selected if: i) the committee is to consist of 3 men and 3 women. ii) there are no restrictions on the number of men and women on the committee. iii) at least one man

$$\mathrm{If}\:\mathrm{a}\:\mathrm{group}\:\mathrm{consist}\:\mathrm{of}\:\mathrm{8}\:\mathrm{men}\:\mathrm{and}\:\mathrm{6}\:\mathrm{women}, \\ $$$$\mathrm{in}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{a}\:\mathrm{committee}\:\mathrm{of} \\ $$$$\mathrm{5}\:\mathrm{be}\:\mathrm{selected}\:\mathrm{if}: \\ $$$$\left.\:\:\:\:\:\:\mathrm{i}\right)\:\mathrm{the}\:\mathrm{committee}\:\mathrm{is}\:\mathrm{to}\:\mathrm{consist}\:\mathrm{of}\:\mathrm{3}\:\mathrm{men} \\ $$$$\mathrm{and}\:\mathrm{3}\:\mathrm{women}. \\ $$$$\left.\:\:\:\:\:\:\mathrm{ii}\right)\:\mathrm{there}\:\mathrm{are}\:\mathrm{no}\:\mathrm{restrictions}\:\mathrm{on}\:\mathrm{the}\: \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{men}\:\mathrm{and}\:\mathrm{women}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{committee}. \\ $$$$\left.\:\:\:\:\:\:\:\mathrm{iii}\right)\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{man} \\ $$

Question Number 149817 Answers: 0 Comments: 0

x^3 −x=c let x=t+h t^3 +3ht^2 +(3h^2 −1)t+h^3 −h−c=0 let t(t^2 +3h^2 −1)=p 3ht^2 +h^3 −h−c=q ⇒ t^2 =((q+c+h−h^3 )/(3h)) p+q=0 (((q+c+h−h^3 )/(3h)))(((q+c+h−h^3 )/(3h))+3h^2 −1)^2 =q^2 ⇒ (q+c+h−h^3 )(q+c−2h+8h^3 )^2 = 27h^3 q^2 let q+c−2h=0 ⇒ 64h^4 (3−h^2 )=27(2h−c)^2 ⇒ 8h^2 (√(3−h^2 ))=3(√3)(2h−c) let h=(√3)sin θ ⇒ 8sin^2 θcos θ=2(√3)sin θ−c 4sin θsin 2θ=2(√3)sin θ−c 2sin θ((√3)−2sin 2θ)=c ......

$$\:\:\:{x}^{\mathrm{3}} −{x}={c} \\ $$$$\:\:{let}\:\:{x}={t}+{h} \\ $$$${t}^{\mathrm{3}} +\mathrm{3}{ht}^{\mathrm{2}} +\left(\mathrm{3}{h}^{\mathrm{2}} −\mathrm{1}\right){t}+{h}^{\mathrm{3}} −{h}−{c}=\mathrm{0} \\ $$$${let}\:\:{t}\left({t}^{\mathrm{2}} +\mathrm{3}{h}^{\mathrm{2}} −\mathrm{1}\right)={p} \\ $$$$\mathrm{3}{ht}^{\mathrm{2}} +{h}^{\mathrm{3}} −{h}−{c}={q} \\ $$$$\Rightarrow\:\:{t}^{\mathrm{2}} =\frac{{q}+{c}+{h}−{h}^{\mathrm{3}} }{\mathrm{3}{h}} \\ $$$${p}+{q}=\mathrm{0} \\ $$$$\left(\frac{{q}+{c}+{h}−{h}^{\mathrm{3}} }{\mathrm{3}{h}}\right)\left(\frac{{q}+{c}+{h}−{h}^{\mathrm{3}} }{\mathrm{3}{h}}+\mathrm{3}{h}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:={q}^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\left({q}+{c}+{h}−{h}^{\mathrm{3}} \right)\left({q}+{c}−\mathrm{2}{h}+\mathrm{8}{h}^{\mathrm{3}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\:\mathrm{27}{h}^{\mathrm{3}} {q}^{\mathrm{2}} \\ $$$${let}\:\:{q}+{c}−\mathrm{2}{h}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{64}{h}^{\mathrm{4}} \left(\mathrm{3}−{h}^{\mathrm{2}} \right)=\mathrm{27}\left(\mathrm{2}{h}−{c}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{8}{h}^{\mathrm{2}} \sqrt{\mathrm{3}−{h}^{\mathrm{2}} }=\mathrm{3}\sqrt{\mathrm{3}}\left(\mathrm{2}{h}−{c}\right) \\ $$$${let}\:\:{h}=\sqrt{\mathrm{3}}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\mathrm{8sin}\:^{\mathrm{2}} \theta\mathrm{cos}\:\theta=\mathrm{2}\sqrt{\mathrm{3}}\mathrm{sin}\:\theta−{c} \\ $$$$\mathrm{4sin}\:\theta\mathrm{sin}\:\mathrm{2}\theta=\mathrm{2}\sqrt{\mathrm{3}}\mathrm{sin}\:\theta−{c} \\ $$$$\mathrm{2sin}\:\theta\left(\sqrt{\mathrm{3}}−\mathrm{2sin}\:\mathrm{2}\theta\right)={c} \\ $$$$...... \\ $$

Question Number 149813 Answers: 1 Comments: 1

∫(−1)^([x]) dx = ?

$$\int\left(−\mathrm{1}\right)^{\left[\boldsymbol{\mathrm{x}}\right]} \:\mathrm{dx}\:=\:? \\ $$

Question Number 149809 Answers: 2 Comments: 0