Question and Answers Forum

AllQuestion and Answers: Page 686

Question Number 149595 Answers: 2 Comments: 1

Question Number 149588 Answers: 2 Comments: 2

{ ((x + (1/y) = 2)),((y + (1/z) = 2)),((z + (1/x) = 2)) :} ⇒ x;y;z=?

$$\begin{cases}{{x}\:+\:\frac{\mathrm{1}}{{y}}\:=\:\mathrm{2}}\\{{y}\:+\:\frac{\mathrm{1}}{{z}}\:=\:\mathrm{2}}\\{{z}\:+\:\frac{\mathrm{1}}{{x}}\:=\:\mathrm{2}}\end{cases}\:\:\:\Rightarrow\:\:{x};{y};{z}=? \\ $$

Question Number 149700 Answers: 2 Comments: 1

Question Number 149585 Answers: 1 Comments: 0

if x;y;z>0 and x^2 +y^2 +z^2 =3 then: Σ ((x^2 +y^2 )/((2x^2 +y^2 )(y^2 +2x^2 ))) ≥ (2/3)

$${if}\:\:{x};{y};{z}>\mathrm{0}\:\:{and}\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\mathrm{3}\:\:{then}: \\ $$$$\Sigma\:\frac{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{\left(\mathrm{2}{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\left({y}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} \right)}\:\geqslant\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Question Number 149569 Answers: 1 Comments: 0

lim_(x→∞) (((5x + 6)/(2x - 9)))^x^2 = ?

$$\underset{\boldsymbol{\mathrm{x}}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{5x}\:+\:\mathrm{6}}{\mathrm{2x}\:-\:\mathrm{9}}\right)^{\boldsymbol{\mathrm{x}}^{\mathrm{2}} } =\:? \\ $$

Question Number 149568 Answers: 1 Comments: 0

solve the equation: 20z[z] - 21{z} = 2021 where {∗} is GIF and {z} = z - [z]

$${solve}\:{the}\:{equation}: \\ $$$$\mathrm{20}{z}\left[{z}\right]\:-\:\mathrm{21}\left\{{z}\right\}\:=\:\mathrm{2021} \\ $$$${where}\:\left\{\ast\right\}\:{is}\:{GIF}\:\:{and}\:\:\left\{{z}\right\}\:=\:{z}\:-\:\left[{z}\right] \\ $$

Question Number 149567 Answers: 0 Comments: 5

if q is prime number fixed, then solve for natural numbers the equation: (1/q) = (1/x) + (1/y) - (1/z)

$${if}\:\:\boldsymbol{{q}}\:\:{is}\:{prime}\:{number}\:{fixed},\:{then} \\ $$$${solve}\:{for}\:{natural}\:{numbers}\:{the}\:{equation}: \\ $$$$\frac{\mathrm{1}}{{q}}\:=\:\frac{\mathrm{1}}{{x}}\:+\:\frac{\mathrm{1}}{{y}}\:-\:\frac{\mathrm{1}}{{z}} \\ $$

Question Number 152596 Answers: 2 Comments: 0

Question Number 149551 Answers: 1 Comments: 0

Question Number 149547 Answers: 1 Comments: 0

Evaluate lim_(x→(π/7)) ((8cos xcos 2xcos 4x+1)/(x−(π/7)))

$$\:\mathrm{Evaluate}\:\underset{{x}\rightarrow\frac{\pi}{\mathrm{7}}} {\mathrm{lim}}\frac{\mathrm{8cos}\:\mathrm{xcos}\:\mathrm{2xcos}\:\mathrm{4x}+\mathrm{1}}{\mathrm{x}−\frac{\pi}{\mathrm{7}}} \\ $$

Question Number 149534 Answers: 2 Comments: 0

Question Number 149532 Answers: 1 Comments: 0

on realise une suite infinie d′epreuves independantes.chaque epreuve resulte en un succes avec la probabilite p∈]0;1[ ou un echec avec la probabilite q=1−p.soit A_n l′evement “obenir au moins un succes au cours des premieres epreuves.” determiner P(A_n )

$${on}\:{realise}\:{une}\:{suite}\:{infinie}\:{d}'{epreuves} \\ $$$${independantes}.{chaque}\:{epreuve}\:{resulte}\:{en} \\ $$$$\left.{un}\:{succes}\:{avec}\:{la}\:{probabilite}\:{p}\in\right]\mathrm{0};\mathrm{1}\left[\:{ou}\:{un}\right. \\ $$$${echec}\:{avec}\:{la}\:{probabilite}\:{q}=\mathrm{1}−{p}.{soit}\:{A}_{{n}} \\ $$$${l}'{evement}\:``{obenir}\:{au}\:{moins}\:{un}\:{succes}\:{au} \\ $$$${cours}\:{des}\:{premieres}\:{epreuves}.''\:{determiner} \\ $$$${P}\left({A}_{{n}} \right) \\ $$

Question Number 149527 Answers: 1 Comments: 1

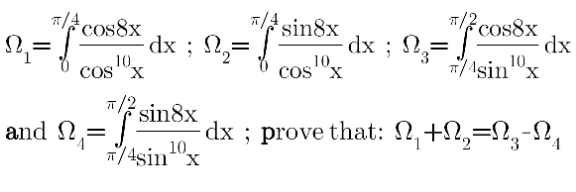
Question Number 149516 Answers: 1 Comments: 0

Ω = ∫_( 0) ^( 3) ((√((x + 2)^2 - 8x))) dx = ?

$$\Omega\:=\:\underset{\:\mathrm{0}} {\overset{\:\mathrm{3}} {\int}}\:\left(\sqrt{\left({x}\:+\:\mathrm{2}\right)^{\mathrm{2}} \:-\:\mathrm{8}{x}}\right)\:{dx}\:=\:? \\ $$

Question Number 149510 Answers: 1 Comments: 7

Question Number 149505 Answers: 3 Comments: 2

lim_(n→∞) (((n + 3)/(n + 1)))^n = ?

$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{n}\:+\:\mathrm{3}}{\mathrm{n}\:+\:\mathrm{1}}\right)^{\mathrm{n}} =\:? \\ $$

Question Number 149503 Answers: 2 Comments: 0

Calcular: 3sin∙(150 - 𝛂) - 2cos∙(60 - 𝛂) = (1/2)

$$\mathrm{Calcular}: \\ $$$$\mathrm{3sin}\centerdot\left(\mathrm{150}\:-\:\boldsymbol{\alpha}\right)\:-\:\mathrm{2cos}\centerdot\left(\mathrm{60}\:-\:\boldsymbol{\alpha}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Question Number 149498 Answers: 2 Comments: 0

∫((px+q)/( (√(x^2 +r^2 ))))

$$ \\ $$$$\int\frac{{px}+{q}}{\:\sqrt{{x}^{\mathrm{2}} +{r}^{\mathrm{2}} }} \\ $$

Question Number 149586 Answers: 0 Comments: 0

$$ \\ $$$$ \\ $$

Question Number 149485 Answers: 2 Comments: 0

proof that 1=2??

$$\mathrm{proof}\:\mathrm{that}\:\mathrm{1}=\mathrm{2}?? \\ $$

Question Number 149481 Answers: 1 Comments: 0

Question Number 149478 Answers: 2 Comments: 2

Solve for real numbers: x^2 −2x−3siny−4cosy + 6 = 0

$${Solve}\:{for}\:{real}\:{numbers}: \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}{sin}\boldsymbol{{y}}−\mathrm{4}{cos}\boldsymbol{{y}}\:+\:\mathrm{6}\:=\:\mathrm{0} \\ $$

Question Number 149474 Answers: 0 Comments: 2

x;y;z≥0 and x+y+z=3 prove that: (x^5 )^(1/(12)) + (y^5 )^(1/(12)) + (z^5 )^(1/(12)) ≥ xy + yz + zx

$${x};{y};{z}\geqslant\mathrm{0}\:\:\mathrm{and}\:\:{x}+{y}+{z}=\mathrm{3}\:\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\sqrt[{\mathrm{12}}]{{x}^{\mathrm{5}} }\:+\:\sqrt[{\mathrm{12}}]{{y}^{\mathrm{5}} }\:+\:\sqrt[{\mathrm{12}}]{{z}^{\mathrm{5}} }\:\geqslant\:{xy}\:+\:{yz}\:+\:{zx} \\ $$

Question Number 149471 Answers: 1 Comments: 0

on distribue au hasard 8 boules b_1 ...b_8 dans 6 tiroirs t_1 ...t_6 .soit A_i l′evenement “le tiroir t_i est vide” les evenements A_1 et A_2 sont-ils independants ?

$${on}\:{distribue}\:{au}\:{hasard}\:\mathrm{8}\:{boules}\:{b}_{\mathrm{1}} ...{b}_{\mathrm{8}} \\ $$$${dans}\:\mathrm{6}\:{tiroirs}\:{t}_{\mathrm{1}} ...{t}_{\mathrm{6}} .{soit}\:{A}_{{i}} \:{l}'{evenement} \\ $$$$``{le}\:{tiroir}\:{t}_{{i}} \:{est}\:{vide}''\:{les}\:{evenements}\:{A}_{\mathrm{1}} {et} \\ $$$${A}_{\mathrm{2}} {sont}-{ils}\:{independants}\:? \\ $$

Question Number 149468 Answers: 1 Comments: 0

sin𝛂 ∙ cos𝛂 = (3/8) ⇒ 3∣sin𝛂 - cos𝛂∣=?

$${sin}\boldsymbol{\alpha}\:\centerdot\:{cos}\boldsymbol{\alpha}\:=\:\frac{\mathrm{3}}{\mathrm{8}}\:\Rightarrow\:\mathrm{3}\mid{sin}\boldsymbol{\alpha}\:-\:{cos}\boldsymbol{\alpha}\mid=? \\ $$

Question Number 149467 Answers: 1 Comments: 0

Pg 681 Pg 682 Pg 683 Pg 684 Pg 685 Pg 686 Pg 687 Pg 688 Pg 689 Pg 690

Contact: info@tinkutara.com