Question and Answers Forum

AllQuestion and Answers: Page 675

Question Number 150647 Answers: 1 Comments: 0

Question Number 150646 Answers: 1 Comments: 0

Let 𝛌∈R fixed.Solve for real numbers: { ((ax + by = 2λ + 1)),((ax^2 + by^2 = 4λ + 1)),((ax^3 + by^3 = 8λ + 1)),((ax^4 + by^4 = 16λ + 1)) :}

$$\boldsymbol{\mathrm{L}}\mathrm{et}\:\boldsymbol{\lambda}\in\mathbb{R}\:\mathrm{fixed}.\boldsymbol{\mathrm{S}}\mathrm{olve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\begin{cases}{\mathrm{ax}\:+\:\mathrm{by}\:=\:\mathrm{2}\lambda\:+\:\mathrm{1}}\\{\mathrm{ax}^{\mathrm{2}} \:+\:\mathrm{by}^{\mathrm{2}} \:=\:\mathrm{4}\lambda\:+\:\mathrm{1}}\\{\mathrm{ax}^{\mathrm{3}} \:+\:\mathrm{by}^{\mathrm{3}} \:=\:\mathrm{8}\lambda\:+\:\mathrm{1}}\\{\mathrm{ax}^{\mathrm{4}} \:+\:\mathrm{by}^{\mathrm{4}} \:=\:\mathrm{16}\lambda\:+\:\mathrm{1}}\end{cases} \\ $$

Question Number 150652 Answers: 0 Comments: 5

If f(3x+1)+f(5x+1)=x^3 -2 Find f(1)+f(4)+f(16)=?

$$\mathrm{If}\:\:\:\mathrm{f}\left(\mathrm{3x}+\mathrm{1}\right)+\mathrm{f}\left(\mathrm{5x}+\mathrm{1}\right)=\mathrm{x}^{\mathrm{3}} -\mathrm{2} \\ $$$$\mathrm{Find}\:\:\mathrm{f}\left(\mathrm{1}\right)+\mathrm{f}\left(\mathrm{4}\right)+\mathrm{f}\left(\mathrm{16}\right)=? \\ $$

Question Number 150641 Answers: 2 Comments: 1

1+(√3^x )=2^x x=?

$$\mathrm{1}+\sqrt{\mathrm{3}^{\mathrm{x}} }=\mathrm{2}^{\mathrm{x}} \\ $$$$\mathrm{x}=? \\ $$

Question Number 150628 Answers: 1 Comments: 0

Question Number 150627 Answers: 1 Comments: 0

∫_0 ^1 (((−1)^(E((1/x))) dx)/x)

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(−\mathrm{1}\right)^{{E}\left(\frac{\mathrm{1}}{{x}}\right)} {dx}}{{x}} \\ $$

Question Number 150626 Answers: 1 Comments: 0

S(x)=Σ_(n=1) ^∞ ln(1+(1/n))x^n S(−1)= ?.. please help..

$${S}\left({x}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right){x}^{{n}} \\ $$$${S}\left(−\mathrm{1}\right)=\:?.. \\ $$$${please}\:{help}.. \\ $$

Question Number 150609 Answers: 0 Comments: 0

I thought this as more basic: ((sinA)/a)=(1/(2R)) ((cosA)/a)=((b^2 +c^2 −a^2 )/(2abc)) ⇒ tanA=((abc)/(R(b^2 +c^2 −a^2 )))

$${I}\:{thought}\:{this}\:{as}\:{more}\:{basic}: \\ $$$$\frac{{sinA}}{{a}}=\frac{\mathrm{1}}{\mathrm{2}{R}} \\ $$$$\frac{{cosA}}{{a}}=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{abc}} \\ $$$$\Rightarrow\:\:\boldsymbol{{tanA}}=\frac{\boldsymbol{{abc}}}{\boldsymbol{{R}}\left(\boldsymbol{{b}}^{\mathrm{2}} +\boldsymbol{{c}}^{\mathrm{2}} −\boldsymbol{{a}}^{\mathrm{2}} \right)} \\ $$

Question Number 150603 Answers: 1 Comments: 0

Compare: x=sin(165°) y=cos(165°) z=tan(165°)

$$\mathrm{Compare}: \\ $$$$\boldsymbol{\mathrm{x}}=\mathrm{sin}\left(\mathrm{165}°\right) \\ $$$$\boldsymbol{\mathrm{y}}=\mathrm{cos}\left(\mathrm{165}°\right) \\ $$$$\boldsymbol{\mathrm{z}}=\mathrm{tan}\left(\mathrm{165}°\right) \\ $$

Question Number 150601 Answers: 1 Comments: 0

Question Number 150600 Answers: 3 Comments: 0

xyz = 10 x + y + z = - 7 xy + xz + yz = 2 Find ((xy)/z) + ((xz)/y) + ((yz)/x) = ?

$$\mathrm{xyz}\:=\:\mathrm{10} \\ $$$$\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{z}\:=\:-\:\mathrm{7} \\ $$$$\mathrm{xy}\:+\:\mathrm{xz}\:+\:\mathrm{yz}\:=\:\mathrm{2} \\ $$$$\mathrm{Find}\:\:\frac{\mathrm{xy}}{\mathrm{z}}\:+\:\frac{\mathrm{xz}}{\mathrm{y}}\:+\:\frac{\mathrm{yz}}{\mathrm{x}}\:=\:? \\ $$

Question Number 150599 Answers: 1 Comments: 2

lim_(x→0) x^x = ?

$$\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{x}}} \:=\:? \\ $$

Question Number 150597 Answers: 1 Comments: 0

Question Number 150596 Answers: 2 Comments: 1

Question Number 150594 Answers: 1 Comments: 0

The function f(x)=e^x +x being differentiable and one to one , has a differentiable inverse f^(−1) (x). The value of (d/dx) (f^(−1) ) at point f(ln 2) is __

$$\mathrm{The}\:\mathrm{function}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{x}} +\mathrm{x}\:\mathrm{being} \\ $$$$\mathrm{differentiable}\:\mathrm{and}\:\mathrm{one}\:\mathrm{to}\:\mathrm{one}\:, \\ $$$$\mathrm{has}\:\mathrm{a}\:\mathrm{differentiable}\:\mathrm{inverse}\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right). \\ $$$$\mathrm{The}\:\mathrm{value}\:\mathrm{of}\:\frac{{d}}{{dx}}\:\left({f}^{−\mathrm{1}} \right)\:\mathrm{at}\:\mathrm{point}\: \\ $$$$\mathrm{f}\left(\mathrm{ln}\:\mathrm{2}\right)\:\mathrm{is}\:\_\_ \\ $$

Question Number 150585 Answers: 0 Comments: 5

lim_(x→0) ((∫_0 ^π cosx^2 dx)/x)=?? Help

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\underset{\mathrm{0}} {\overset{\pi} {\int}}{cosx}^{\mathrm{2}} {dx}}{{x}}=?? \\ $$$${Help} \\ $$

Question Number 150590 Answers: 1 Comments: 0

Let g is the inverse function of f and f ′(x)=(x^(10) /(1+x^2 )). If g(2)= a then g ′(2) =__

$$\mathrm{Let}\:\mathrm{g}\:\mathrm{is}\:\mathrm{the}\:\mathrm{inverse}\:\mathrm{function}\:\mathrm{of} \\ $$$$\mathrm{f}\:\mathrm{and}\:\mathrm{f}\:'\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{10}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }.\:\mathrm{If}\:\mathrm{g}\left(\mathrm{2}\right)=\:{a}\:\mathrm{then} \\ $$$$\mathrm{g}\:'\left(\mathrm{2}\right)\:=\_\_\: \\ $$

Question Number 150571 Answers: 3 Comments: 0

Find A and prove that 2021∈A if abcd^(−) ∈A, (a/(d + 1)) = ((c - b)/c) = ((a + b)/(b + c))

$$\mathrm{Find}\:\boldsymbol{\mathrm{A}}\:\mathrm{and}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{2021}\in\boldsymbol{\mathrm{A}}\:\mathrm{if} \\ $$$$\overline {\mathrm{abcd}}\in\boldsymbol{\mathrm{A}},\:\:\frac{\mathrm{a}}{\mathrm{d}\:+\:\mathrm{1}}\:=\:\frac{\mathrm{c}\:-\:\mathrm{b}}{\mathrm{c}}\:=\:\frac{\mathrm{a}\:+\:\mathrm{b}}{\mathrm{b}\:+\:\mathrm{c}} \\ $$

Question Number 150567 Answers: 4 Comments: 0

Question Number 150560 Answers: 3 Comments: 0

Question Number 150559 Answers: 1 Comments: 0

Solve for natural numbers: x^3 + y^4 = 2022

$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{natural}\:\mathrm{numbers}: \\ $$$$\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{y}^{\mathrm{4}} \:=\:\mathrm{2022} \\ $$

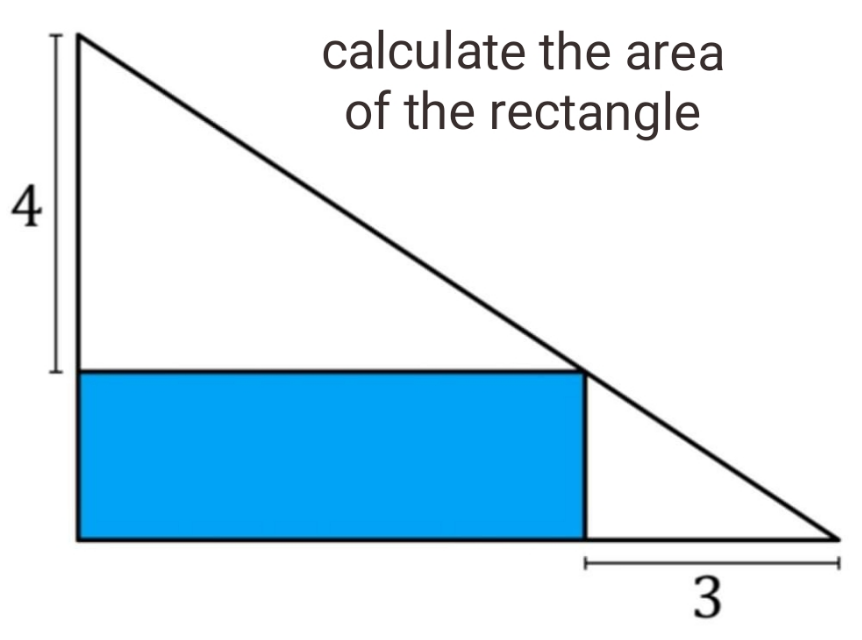
Question Number 150558 Answers: 1 Comments: 0

Solve for integers: (6x + 5y^2 )(4z + x)(2y^2 + 3z) = 2021

$$\mathrm{Solve}\:\mathrm{for}\:\mathrm{integers}: \\ $$$$\left(\mathrm{6x}\:+\:\mathrm{5y}^{\mathrm{2}} \right)\left(\mathrm{4z}\:+\:\mathrm{x}\right)\left(\mathrm{2y}^{\mathrm{2}} \:+\:\mathrm{3z}\right)\:=\:\mathrm{2021} \\ $$

Question Number 150554 Answers: 1 Comments: 0

Show that n_C_r =((n(n−1)(n−2)...(n−r+1))/(r!))

$$\mathrm{Show}\:\mathrm{that}\:\mathrm{n}_{\mathrm{C}_{\mathrm{r}} } =\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)...\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)}{\mathrm{r}!} \\ $$

Question Number 150550 Answers: 0 Comments: 3

Question Number 150549 Answers: 0 Comments: 0

Prove that: ∀n∈N Π_(k=1) ^n k! ∙ k^(n−k+1) ≤ (((n+2)/3))^(n∙(n+1))

$$\mathrm{Prove}\:\mathrm{that}:\:\:\forall\mathrm{n}\in\mathbb{N} \\ $$$$\underset{\boldsymbol{\mathrm{k}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\prod}}\mathrm{k}!\:\centerdot\:\mathrm{k}^{\boldsymbol{\mathrm{n}}−\boldsymbol{\mathrm{k}}+\mathrm{1}} \:\leqslant\:\left(\frac{\mathrm{n}+\mathrm{2}}{\mathrm{3}}\right)^{\boldsymbol{\mathrm{n}}\centerdot\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)} \\ $$

Question Number 150548 Answers: 0 Comments: 0

For k<N fixed and 𝛂>0 then: lim_(n→∞) (1/( (√n^𝛂 ))) ∙ (((Π_(i=1) ^k (n+k+i))/(Π_(i=1) ^k (n+i))))^n^𝛂

$$\mathrm{For}\:\:\boldsymbol{\mathrm{k}}<\mathbb{N}\:\:\mathrm{fixed}\:\:\mathrm{and}\:\:\boldsymbol{\alpha}>\mathrm{0}\:\:\mathrm{then}: \\ $$$$\underset{\boldsymbol{\mathrm{n}}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}^{\boldsymbol{\alpha}} }}\:\centerdot\:\left(\frac{\underset{\boldsymbol{\mathrm{i}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{k}}} {\prod}}\left(\mathrm{n}+\mathrm{k}+\mathrm{i}\right)}{\underset{\boldsymbol{\mathrm{i}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{k}}} {\prod}}\left(\mathrm{n}+\mathrm{i}\right)}\right)^{\boldsymbol{\mathrm{n}}^{\boldsymbol{\alpha}} } \\ $$

Pg 670 Pg 671 Pg 672 Pg 673 Pg 674 Pg 675 Pg 676 Pg 677 Pg 678 Pg 679

Contact: info@tinkutara.com