Question and Answers Forum

AllQuestion and Answers: Page 674

Question Number 151064 Answers: 0 Comments: 0

Calculate :: ∫_0 ^π arctan(((2sin^2 x)/(1−2(√2)ϕcos x+2ϕ^2 )))dx=πarctan (√ϕ) (ϕ=(((√5)−1)/2))

$$\mathrm{Calculate}\:\:::\:\:\int_{\mathrm{0}} ^{\pi} \mathrm{arctan}\left(\frac{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}\varphi\mathrm{cos}\:\mathrm{x}+\mathrm{2}\varphi^{\mathrm{2}} }\right)\mathrm{dx}=\pi\mathrm{arctan}\:\sqrt{\varphi}\:\:\:\:\:\:\:\:\:\:\left(\varphi=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right) \\ $$

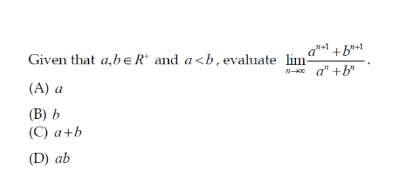
Question Number 151063 Answers: 0 Comments: 0

Calculate :: ∫_0 ^∞ ((ln(1+x))/((π^2 +ln^2 x)x))dx=γ

$$\mathrm{Calculate}\:\:::\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\left(\pi^{\mathrm{2}} +\mathrm{ln}^{\mathrm{2}} \mathrm{x}\right)\mathrm{x}}\mathrm{dx}=\gamma \\ $$

Question Number 151062 Answers: 0 Comments: 0

Calculate :: ∫_0 ^∞ (dx/( (√(x^2 +x))∙((8x^2 +8x+1))^(1/4) ))=((Γ^2 ((1/8)))/(2^((11)/4) Γ((1/4))))

$$\mathrm{Calculate}\:\:::\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\centerdot\sqrt[{\mathrm{4}}]{\mathrm{8x}^{\mathrm{2}} +\mathrm{8x}+\mathrm{1}}}=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{8}}\right)}{\mathrm{2}^{\frac{\mathrm{11}}{\mathrm{4}}} \Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$

Question Number 151061 Answers: 0 Comments: 0

Calculate :: ∫_0 ^(π/2) x∙cot x∙ln^2 cos xdx=(π^3 /(24))ln2+(π/6)ln^3 2−(3/(16))πζ(3)

$$\mathrm{Calculate}\:\:::\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{x}\centerdot\mathrm{cot}\:\mathrm{x}\centerdot\mathrm{ln}^{\mathrm{2}} \mathrm{cos}\:\mathrm{xdx}=\frac{\pi^{\mathrm{3}} }{\mathrm{24}}\mathrm{ln2}+\frac{\pi}{\mathrm{6}}\mathrm{ln}^{\mathrm{3}} \mathrm{2}−\frac{\mathrm{3}}{\mathrm{16}}\pi\zeta\left(\mathrm{3}\right) \\ $$

Question Number 151060 Answers: 0 Comments: 0

Calculate :: ∫_0 ^∞ ((x(√x))/((x^2 +1)(1+ax)))dx=((a^2 −a+(√(2a)))/( (√2)a(1+a^2 )))π ,(a>0)

$$\mathrm{Calculate}\:::\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}\sqrt{\mathrm{x}}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}+\mathrm{ax}\right)}\mathrm{dx}=\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{a}+\sqrt{\mathrm{2a}}}{\:\sqrt{\mathrm{2}}\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\pi\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:,\left(\mathrm{a}>\mathrm{0}\right) \\ $$

Question Number 151059 Answers: 0 Comments: 0

((((x−2))^(1/3) +2))^(1/3) + ((2−((x+2))^(1/3) ))^(1/3) = 2 x =?

$$\:\:\:\:\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{2}}\:+\mathrm{2}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt[{\mathrm{3}}]{\mathrm{x}+\mathrm{2}}}\:=\:\mathrm{2}\: \\ $$$$\:\:\:\:\mathrm{x}\:=? \\ $$

Question Number 151052 Answers: 1 Comments: 0

if a;b;c positive real numbers and (a/(1+a)) + (b/(1+b)) + (c/(1+c)) = 1 prove that: abc ≤ (1/8)

$$\mathrm{if}\:\:\:\mathrm{a};\mathrm{b};\mathrm{c}\:\:\:\mathrm{positive}\:\mathrm{real}\:\mathrm{numbers}\:\:\mathrm{and} \\ $$$$\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}}\:+\:\frac{\mathrm{b}}{\mathrm{1}+\mathrm{b}}\:+\:\frac{\mathrm{c}}{\mathrm{1}+\mathrm{c}}\:=\:\mathrm{1}\:\:\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\mathrm{abc}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$

Question Number 151045 Answers: 0 Comments: 0

Question Number 151043 Answers: 2 Comments: 0

Solve the system: { ((y = ((2x)/(1−x^2 )))),((z = ((2y)/(1−y^2 )))),((x = ((2z)/(1−z^2 )))) :}

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{system}: \\ $$$$\begin{cases}{\boldsymbol{\mathrm{y}}\:=\:\frac{\mathrm{2x}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\\{\boldsymbol{\mathrm{z}}\:=\:\frac{\mathrm{2y}}{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }}\\{\boldsymbol{\mathrm{x}}\:=\:\frac{\mathrm{2z}}{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }}\end{cases} \\ $$

Question Number 151042 Answers: 0 Comments: 1

if (√((9)^(1/3) − 1)) + (√(((16))^(1/3) − (4)^(1/3) )) = (√x) ; x∈Z find x=?

$$\mathrm{if}\:\:\sqrt{\sqrt[{\mathrm{3}}]{\mathrm{9}}\:−\:\mathrm{1}}\:+\:\sqrt{\sqrt[{\mathrm{3}}]{\mathrm{16}}\:−\:\sqrt[{\mathrm{3}}]{\mathrm{4}}}\:=\:\sqrt{\boldsymbol{\mathrm{x}}}\:\:;\:\:\boldsymbol{\mathrm{x}}\in\mathbb{Z} \\ $$$$\mathrm{find}\:\:\boldsymbol{\mathrm{x}}=? \\ $$

Question Number 151037 Answers: 1 Comments: 0

Σ_(r=1,r≠s) ^n Σ_(s=1) ^n ((rs)/(n(n−1)))=^? (((n+1)(3n+2))/(12))

$$\underset{\mathrm{r}=\mathrm{1},\mathrm{r}\neq\mathrm{s}} {\overset{\mathrm{n}} {\sum}}\:\:\underset{\mathrm{s}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{rs}}{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}\overset{?} {=}\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{3n}+\mathrm{2}\right)}{\mathrm{12}} \\ $$

Question Number 151036 Answers: 0 Comments: 0

$$ \\ $$

Question Number 151034 Answers: 0 Comments: 0

Question Number 151035 Answers: 0 Comments: 0

determinant ((,),(,))

$$\begin{vmatrix}{}&{}\\{}&{}\end{vmatrix} \\ $$

Question Number 151029 Answers: 0 Comments: 0

Question Number 151028 Answers: 1 Comments: 0

Question Number 151026 Answers: 1 Comments: 0

Σ_(n=0) ^∞ (0^n /(n!))=?

$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{0}^{\mathrm{n}} }{\mathrm{n}!}=? \\ $$

Question Number 151053 Answers: 1 Comments: 0

Question Number 151017 Answers: 0 Comments: 0

∫_0 ^( ∞) (ln(x^(√x) −1))^(−x) dx = ?

$$\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\left(\mathrm{ln}\left({x}^{\sqrt{{x}}} −\mathrm{1}\right)\right)^{−{x}} \:{dx}\:=\:? \\ $$$$\: \\ $$$$\: \\ $$

Question Number 151015 Answers: 0 Comments: 1

Question Number 151013 Answers: 1 Comments: 0

If log(logx)^(((3log(logx))/(log(log(logx)))) ) = 27 Find x=?

$$\mathrm{If}\:\:\mathrm{log}\left(\mathrm{log}\boldsymbol{\mathrm{x}}\right)^{\frac{\mathrm{3}\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{logx}}\right)}{\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{log}}\left(\boldsymbol{\mathrm{logx}}\right)\right)}\:} \:=\:\mathrm{27} \\ $$$$\mathrm{Find}\:\:\boldsymbol{\mathrm{x}}=? \\ $$

Question Number 151010 Answers: 1 Comments: 1

Question Number 151001 Answers: 2 Comments: 0

lim_(x→0) ((((2+sin^2 x))^(1/3) −((1+cos 2x))^(1/3) )/(x tan x)) =?

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{2}+\mathrm{sin}\:^{\mathrm{2}} {x}}−\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{cos}\:\mathrm{2}{x}}}{{x}\:\mathrm{tan}\:{x}}\:=?\: \\ $$$$\:\:\: \\ $$

Question Number 150994 Answers: 0 Comments: 0

show that the improper integral lim_(B→∞) ∫_0 ^( B) sin(x)sin(x^2 )dx converges

$$\: \\ $$$$\:\:\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{improper}\:\mathrm{integral} \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\:\underset{{B}\rightarrow\infty} {\mathrm{lim}}\:\:\int_{\mathrm{0}} ^{\:{B}} \:\mathrm{sin}\left({x}\right)\mathrm{sin}\left({x}^{\mathrm{2}} \right){dx} \\ $$$$\:\: \\ $$$$\:\:\:\mathrm{converges} \\ $$$$\: \\ $$

Question Number 150993 Answers: 1 Comments: 1

∫_0 ^( 1) ((ln(x+1))/(x^2 +1)) dx = ?

$$\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{ln}\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}\:{dx}\:=\:? \\ $$$$\: \\ $$$$\: \\ $$

Question Number 150992 Answers: 2 Comments: 1

∫_0 ^( ∞) (x/(e^x −1)) dx = ?

$$\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{x}}{{e}^{{x}} −\mathrm{1}}\:{dx}\:=\:? \\ $$$$\: \\ $$$$\: \\ $$

Pg 669 Pg 670 Pg 671 Pg 672 Pg 673 Pg 674 Pg 675 Pg 676 Pg 677 Pg 678

Contact: info@tinkutara.com