
AllQuestion and Answers: Page 672
Question Number 152617 Answers: 0 Comments: 1

Question Number 152608 Answers: 2 Comments: 0
Question Number 152588 Answers: 3 Comments: 0
Question Number 152580 Answers: 1 Comments: 0

Question Number 152576 Answers: 0 Comments: 1
Question Number 152572 Answers: 1 Comments: 0
Question Number 152571 Answers: 1 Comments: 0
Question Number 152620 Answers: 1 Comments: 1

Question Number 152555 Answers: 2 Comments: 0
Question Number 152551 Answers: 1 Comments: 0
Question Number 152546 Answers: 1 Comments: 0
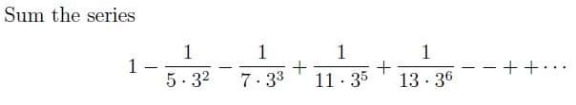
Question Number 152545 Answers: 1 Comments: 0

Question Number 152536 Answers: 1 Comments: 2
Question Number 152533 Answers: 1 Comments: 0

Question Number 152532 Answers: 1 Comments: 0

Question Number 152522 Answers: 1 Comments: 2

Question Number 152791 Answers: 1 Comments: 0
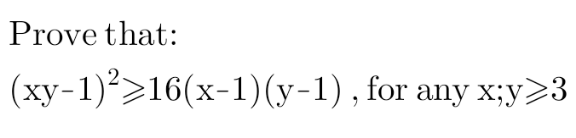
Question Number 152513 Answers: 1 Comments: 1
$$\int\:\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{8}}\:{dx}\:=? \\ $$
Question Number 152502 Answers: 1 Comments: 0
Question Number 152500 Answers: 0 Comments: 0

Question Number 152498 Answers: 0 Comments: 3
Question Number 152496 Answers: 1 Comments: 0
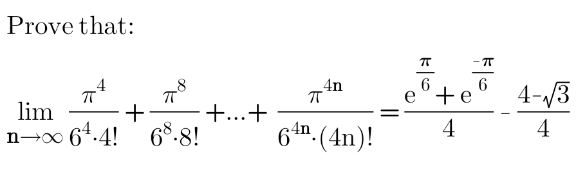
Question Number 152494 Answers: 1 Comments: 0
Question Number 152543 Answers: 2 Comments: 0
Question Number 152486 Answers: 1 Comments: 0

Question Number 152544 Answers: 2 Comments: 1
Pg 667 Pg 668 Pg 669 Pg 670 Pg 671 Pg 672 Pg 673 Pg 674 Pg 675 Pg 676
