
AllQuestion and Answers: Page 671
Question Number 152723 Answers: 1 Comments: 0
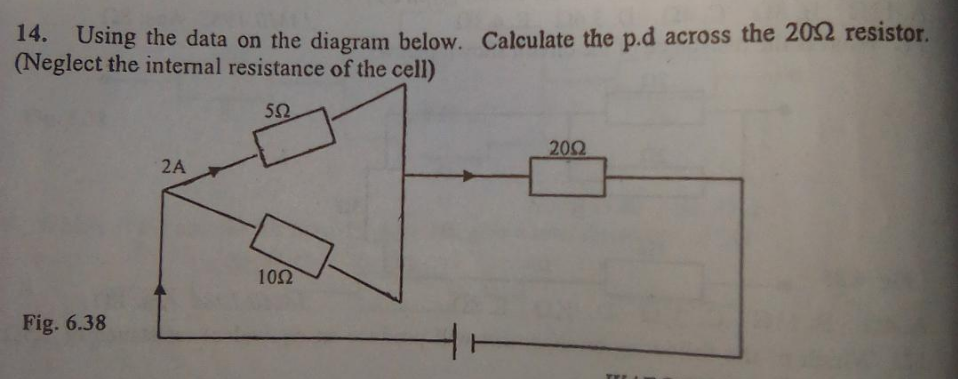
Question Number 152722 Answers: 1 Comments: 0

Question Number 152721 Answers: 0 Comments: 2

Question Number 152788 Answers: 0 Comments: 0
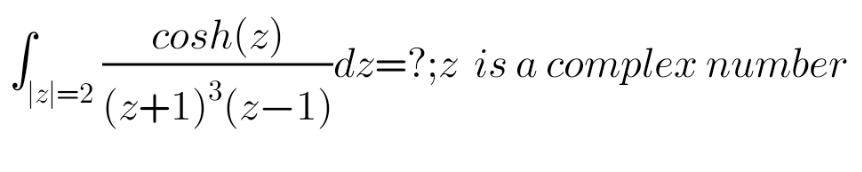
Question Number 152790 Answers: 0 Comments: 1
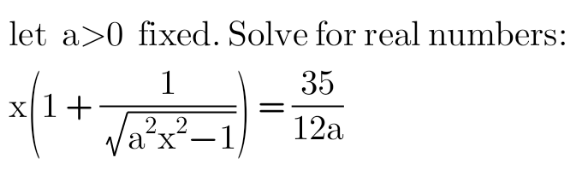
Question Number 152714 Answers: 0 Comments: 0
Question Number 152797 Answers: 1 Comments: 0
Question Number 152712 Answers: 0 Comments: 0

Question Number 152703 Answers: 2 Comments: 0
Question Number 152701 Answers: 0 Comments: 0
Question Number 152697 Answers: 0 Comments: 0
Question Number 152715 Answers: 0 Comments: 2
Question Number 152692 Answers: 0 Comments: 0
Question Number 152691 Answers: 1 Comments: 0
Question Number 152683 Answers: 1 Comments: 0
Question Number 152682 Answers: 1 Comments: 0

Question Number 152672 Answers: 1 Comments: 0
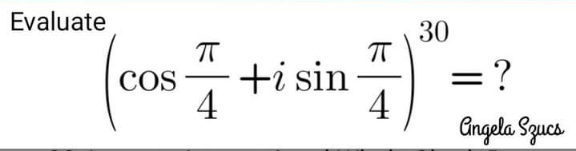
Question Number 152671 Answers: 3 Comments: 2
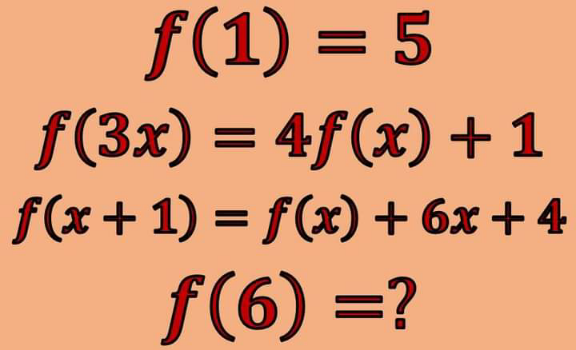
Question Number 152670 Answers: 1 Comments: 0

Question Number 152678 Answers: 2 Comments: 0
Question Number 152663 Answers: 1 Comments: 0
Question Number 152660 Answers: 1 Comments: 0
Question Number 152653 Answers: 1 Comments: 0
Question Number 152652 Answers: 0 Comments: 1

Question Number 152647 Answers: 1 Comments: 1

Question Number 152631 Answers: 1 Comments: 0

Pg 666 Pg 667 Pg 668 Pg 669 Pg 670 Pg 671 Pg 672 Pg 673 Pg 674 Pg 675
