Question and Answers Forum

AllQuestion and Answers: Page 670

Question Number 151074 Answers: 1 Comments: 0

5+5+5

$$\mathrm{5}+\mathrm{5}+\mathrm{5} \\ $$

Question Number 151070 Answers: 0 Comments: 4

a+b+c=30 and a;b;c>0 find the minimum value of (1/a) + (1/b) + (1/c)

$$\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{30}\:\:\:\mathrm{and}\:\:\:\mathrm{a};\mathrm{b};\mathrm{c}>\mathrm{0} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of} \\ $$$$\frac{\mathrm{1}}{\mathrm{a}}\:+\:\frac{\mathrm{1}}{\mathrm{b}}\:+\:\frac{\mathrm{1}}{\mathrm{c}} \\ $$

Question Number 151069 Answers: 0 Comments: 0

Calculate :: ∫_0 ^∞ ((sin (1145141919810893x))/(x(cosh x+cos x)))dx=(π/4)

$$\mathrm{Calculate}\:\:::\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{sin}\:\left(\mathrm{1145141919810893x}\right)}{\mathrm{x}\left(\mathrm{cosh}\:\mathrm{x}+\mathrm{cos}\:\mathrm{x}\right)}\mathrm{dx}=\frac{\pi}{\mathrm{4}} \\ $$

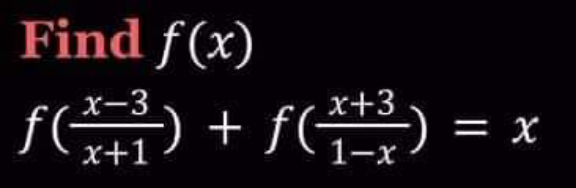
Question Number 151068 Answers: 0 Comments: 0

Calculate :: ∫_0 ^∞ ((√x)/((x^4 +14x^2 +1)^(5/4) ))dx=((Γ^2 ((3/4)))/(4(√(2π))))

$$\mathrm{Calculate}\:\:::\:\int_{\mathrm{0}} ^{\infty} \frac{\sqrt{\mathrm{x}}}{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{14x}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{5}}{\mathrm{4}}} }\mathrm{dx}=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)}{\mathrm{4}\sqrt{\mathrm{2}\pi}} \\ $$

Question Number 151067 Answers: 0 Comments: 0

Calculate :: ∫_0 ^π sin (x/2)∙arctan((2/(sin x))−1)dx=(√2)ln(1+(√2))+(1−(1/( (√2))))π

$$\mathrm{Calculate}\:\:::\:\:\int_{\mathrm{0}} ^{\pi} \mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\centerdot\mathrm{arctan}\left(\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{x}}−\mathrm{1}\right)\mathrm{dx}=\sqrt{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\pi \\ $$

Question Number 151066 Answers: 0 Comments: 0

Calculate :: ∫_0 ^(π/2) (arctan(((sin x)/2))+arctan(((cos 3x+15cos x)/8)))dx =(π^2 /4)−ln^2 (1+(√2))

$$\mathrm{Calculate}\:\:::\:\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{arctan}\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{2}}\right)+\mathrm{arctan}\left(\frac{\mathrm{cos}\:\mathrm{3x}+\mathrm{15cos}\:\mathrm{x}}{\mathrm{8}}\right)\right)\mathrm{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$

Question Number 151065 Answers: 0 Comments: 0

Calculate :: ∫_(−∞) ^(+∞) ((Γ(x))/(Γ(x+a)))sin (πx)dx=(2^(a−1) /(Γ(a)))π (a>0)

$$\mathrm{Calculate}\:\:\:::\:\:\int_{−\infty} ^{+\infty} \frac{\Gamma\left(\mathrm{x}\right)}{\Gamma\left(\mathrm{x}+\mathrm{a}\right)}\mathrm{sin}\:\left(\pi\mathrm{x}\right)\mathrm{dx}=\frac{\mathrm{2}^{\mathrm{a}−\mathrm{1}} }{\Gamma\left(\mathrm{a}\right)}\pi\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{a}>\mathrm{0}\right) \\ $$

Question Number 151064 Answers: 0 Comments: 0

Calculate :: ∫_0 ^π arctan(((2sin^2 x)/(1−2(√2)ϕcos x+2ϕ^2 )))dx=πarctan (√ϕ) (ϕ=(((√5)−1)/2))

$$\mathrm{Calculate}\:\:::\:\:\int_{\mathrm{0}} ^{\pi} \mathrm{arctan}\left(\frac{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}\varphi\mathrm{cos}\:\mathrm{x}+\mathrm{2}\varphi^{\mathrm{2}} }\right)\mathrm{dx}=\pi\mathrm{arctan}\:\sqrt{\varphi}\:\:\:\:\:\:\:\:\:\:\left(\varphi=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}\right) \\ $$

Question Number 151063 Answers: 0 Comments: 0

Calculate :: ∫_0 ^∞ ((ln(1+x))/((π^2 +ln^2 x)x))dx=γ

$$\mathrm{Calculate}\:\:::\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\left(\pi^{\mathrm{2}} +\mathrm{ln}^{\mathrm{2}} \mathrm{x}\right)\mathrm{x}}\mathrm{dx}=\gamma \\ $$

Question Number 151062 Answers: 0 Comments: 0

Calculate :: ∫_0 ^∞ (dx/( (√(x^2 +x))∙((8x^2 +8x+1))^(1/4) ))=((Γ^2 ((1/8)))/(2^((11)/4) Γ((1/4))))

$$\mathrm{Calculate}\:\:::\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}\centerdot\sqrt[{\mathrm{4}}]{\mathrm{8x}^{\mathrm{2}} +\mathrm{8x}+\mathrm{1}}}=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{8}}\right)}{\mathrm{2}^{\frac{\mathrm{11}}{\mathrm{4}}} \Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$

Question Number 151061 Answers: 0 Comments: 0

Calculate :: ∫_0 ^(π/2) x∙cot x∙ln^2 cos xdx=(π^3 /(24))ln2+(π/6)ln^3 2−(3/(16))πζ(3)

$$\mathrm{Calculate}\:\:::\:\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{x}\centerdot\mathrm{cot}\:\mathrm{x}\centerdot\mathrm{ln}^{\mathrm{2}} \mathrm{cos}\:\mathrm{xdx}=\frac{\pi^{\mathrm{3}} }{\mathrm{24}}\mathrm{ln2}+\frac{\pi}{\mathrm{6}}\mathrm{ln}^{\mathrm{3}} \mathrm{2}−\frac{\mathrm{3}}{\mathrm{16}}\pi\zeta\left(\mathrm{3}\right) \\ $$

Question Number 151060 Answers: 0 Comments: 0

Calculate :: ∫_0 ^∞ ((x(√x))/((x^2 +1)(1+ax)))dx=((a^2 −a+(√(2a)))/( (√2)a(1+a^2 )))π ,(a>0)

$$\mathrm{Calculate}\:::\:\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}\sqrt{\mathrm{x}}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{1}+\mathrm{ax}\right)}\mathrm{dx}=\frac{\mathrm{a}^{\mathrm{2}} −\mathrm{a}+\sqrt{\mathrm{2a}}}{\:\sqrt{\mathrm{2}}\mathrm{a}\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \right)}\pi\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:,\left(\mathrm{a}>\mathrm{0}\right) \\ $$

Question Number 151059 Answers: 0 Comments: 0

((((x−2))^(1/3) +2))^(1/3) + ((2−((x+2))^(1/3) ))^(1/3) = 2 x =?

$$\:\:\:\:\sqrt[{\mathrm{3}}]{\sqrt[{\mathrm{3}}]{\mathrm{x}−\mathrm{2}}\:+\mathrm{2}}\:+\:\sqrt[{\mathrm{3}}]{\mathrm{2}−\sqrt[{\mathrm{3}}]{\mathrm{x}+\mathrm{2}}}\:=\:\mathrm{2}\: \\ $$$$\:\:\:\:\mathrm{x}\:=? \\ $$

Question Number 151052 Answers: 1 Comments: 0

if a;b;c positive real numbers and (a/(1+a)) + (b/(1+b)) + (c/(1+c)) = 1 prove that: abc ≤ (1/8)

$$\mathrm{if}\:\:\:\mathrm{a};\mathrm{b};\mathrm{c}\:\:\:\mathrm{positive}\:\mathrm{real}\:\mathrm{numbers}\:\:\mathrm{and} \\ $$$$\frac{\mathrm{a}}{\mathrm{1}+\mathrm{a}}\:+\:\frac{\mathrm{b}}{\mathrm{1}+\mathrm{b}}\:+\:\frac{\mathrm{c}}{\mathrm{1}+\mathrm{c}}\:=\:\mathrm{1}\:\:\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\mathrm{abc}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$

Question Number 151045 Answers: 0 Comments: 0

Question Number 151043 Answers: 2 Comments: 0

Solve the system: { ((y = ((2x)/(1−x^2 )))),((z = ((2y)/(1−y^2 )))),((x = ((2z)/(1−z^2 )))) :}

$$\mathrm{Solve}\:\mathrm{the}\:\mathrm{system}: \\ $$$$\begin{cases}{\boldsymbol{\mathrm{y}}\:=\:\frac{\mathrm{2x}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\\{\boldsymbol{\mathrm{z}}\:=\:\frac{\mathrm{2y}}{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }}\\{\boldsymbol{\mathrm{x}}\:=\:\frac{\mathrm{2z}}{\mathrm{1}−\mathrm{z}^{\mathrm{2}} }}\end{cases} \\ $$

Question Number 151042 Answers: 0 Comments: 1

if (√((9)^(1/3) − 1)) + (√(((16))^(1/3) − (4)^(1/3) )) = (√x) ; x∈Z find x=?

$$\mathrm{if}\:\:\sqrt{\sqrt[{\mathrm{3}}]{\mathrm{9}}\:−\:\mathrm{1}}\:+\:\sqrt{\sqrt[{\mathrm{3}}]{\mathrm{16}}\:−\:\sqrt[{\mathrm{3}}]{\mathrm{4}}}\:=\:\sqrt{\boldsymbol{\mathrm{x}}}\:\:;\:\:\boldsymbol{\mathrm{x}}\in\mathbb{Z} \\ $$$$\mathrm{find}\:\:\boldsymbol{\mathrm{x}}=? \\ $$

Question Number 151037 Answers: 1 Comments: 0

Σ_(r=1,r≠s) ^n Σ_(s=1) ^n ((rs)/(n(n−1)))=^? (((n+1)(3n+2))/(12))

$$\underset{\mathrm{r}=\mathrm{1},\mathrm{r}\neq\mathrm{s}} {\overset{\mathrm{n}} {\sum}}\:\:\underset{\mathrm{s}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{rs}}{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}\overset{?} {=}\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{3n}+\mathrm{2}\right)}{\mathrm{12}} \\ $$

Question Number 151036 Answers: 0 Comments: 0

$$ \\ $$

Question Number 151034 Answers: 0 Comments: 0

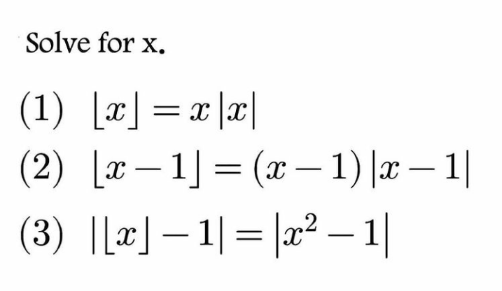
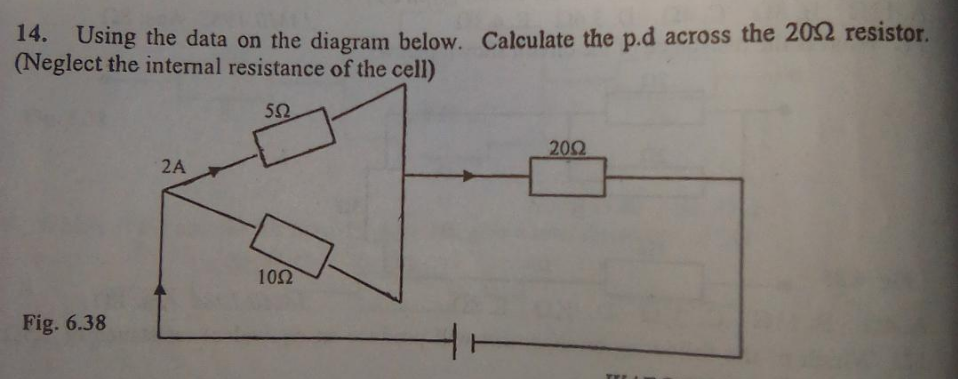
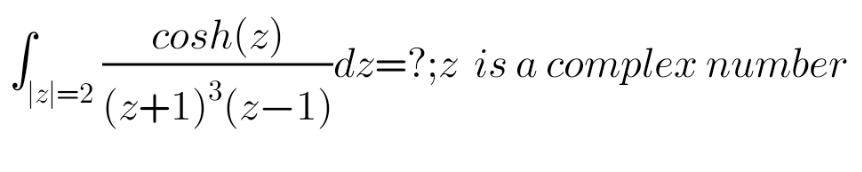
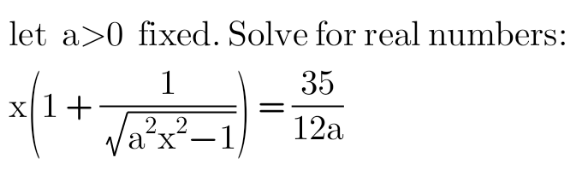
Question Number 151035 Answers: 0 Comments: 0

determinant ((,),(,))

$$\begin{vmatrix}{}&{}\\{}&{}\end{vmatrix} \\ $$

Question Number 151029 Answers: 0 Comments: 0

Question Number 151028 Answers: 1 Comments: 0

Question Number 151026 Answers: 1 Comments: 0

Σ_(n=0) ^∞ (0^n /(n!))=?

$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{0}^{\mathrm{n}} }{\mathrm{n}!}=? \\ $$

Question Number 151053 Answers: 1 Comments: 0

Question Number 151017 Answers: 0 Comments: 0

∫_0 ^( ∞) (ln(x^(√x) −1))^(−x) dx = ?

$$\: \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\left(\mathrm{ln}\left({x}^{\sqrt{{x}}} −\mathrm{1}\right)\right)^{−{x}} \:{dx}\:=\:? \\ $$$$\: \\ $$$$\: \\ $$

Pg 665 Pg 666 Pg 667 Pg 668 Pg 669 Pg 670 Pg 671 Pg 672 Pg 673 Pg 674

Contact: info@tinkutara.com