
AllQuestion and Answers: Page 669
Question Number 152900 Answers: 1 Comments: 0

Question Number 152899 Answers: 0 Comments: 0

Question Number 152898 Answers: 1 Comments: 2

Question Number 153130 Answers: 1 Comments: 0
Question Number 152892 Answers: 0 Comments: 2
Question Number 152889 Answers: 0 Comments: 7
Question Number 152887 Answers: 1 Comments: 0
Question Number 154210 Answers: 0 Comments: 2

Question Number 152881 Answers: 0 Comments: 0
Question Number 152879 Answers: 0 Comments: 3
Question Number 152904 Answers: 5 Comments: 0

Question Number 152903 Answers: 5 Comments: 0
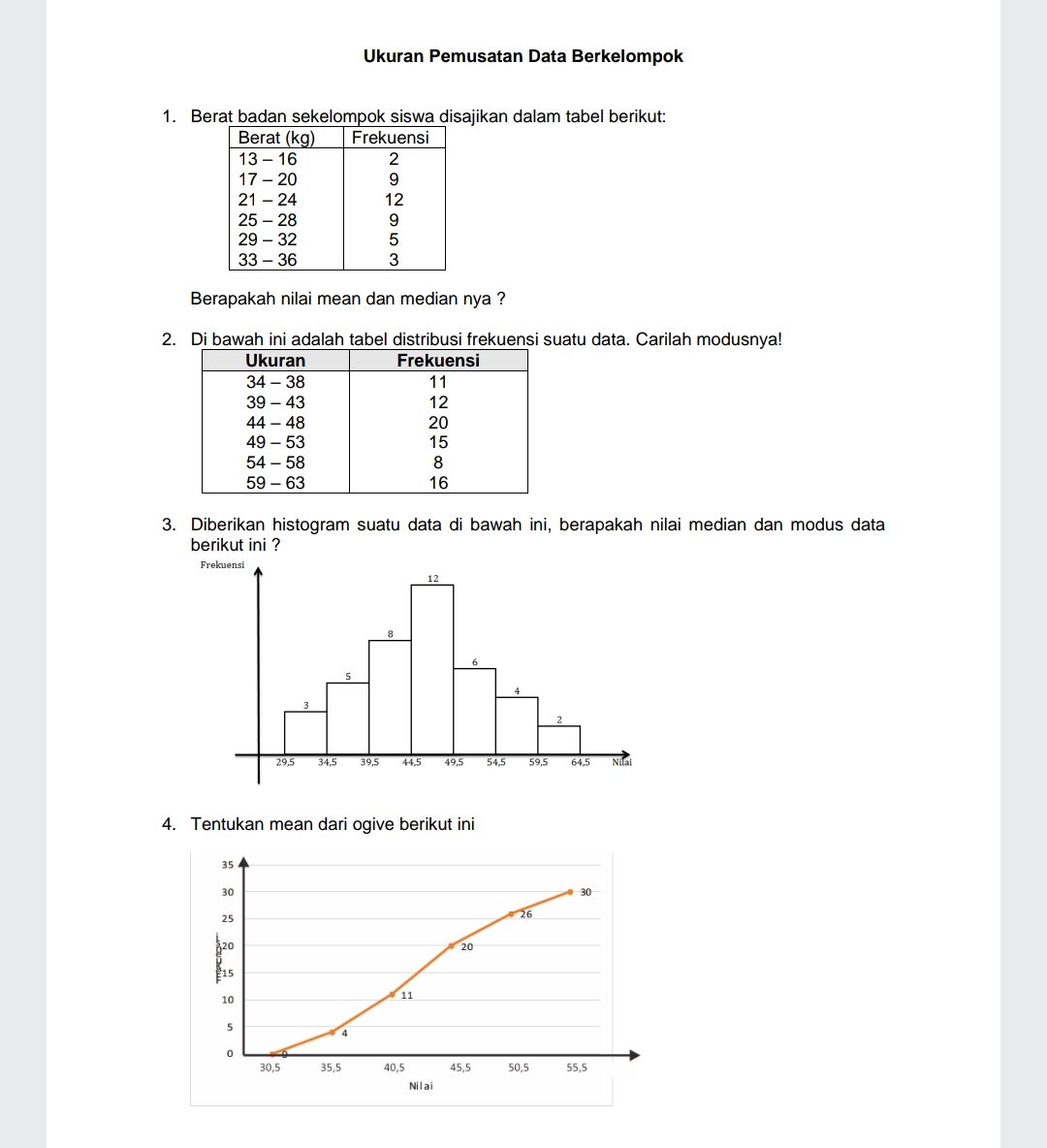
Question Number 152874 Answers: 2 Comments: 0
Question Number 152863 Answers: 1 Comments: 1
Question Number 152861 Answers: 0 Comments: 0
Question Number 152866 Answers: 0 Comments: 0
Question Number 152857 Answers: 0 Comments: 0
Question Number 152848 Answers: 0 Comments: 5
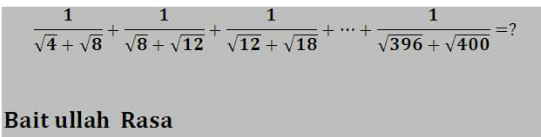
Question Number 152845 Answers: 0 Comments: 0

Question Number 152844 Answers: 1 Comments: 0
Question Number 152841 Answers: 2 Comments: 0

Question Number 152840 Answers: 1 Comments: 0

Question Number 152839 Answers: 0 Comments: 0
Question Number 152834 Answers: 0 Comments: 0

Question Number 152829 Answers: 2 Comments: 0
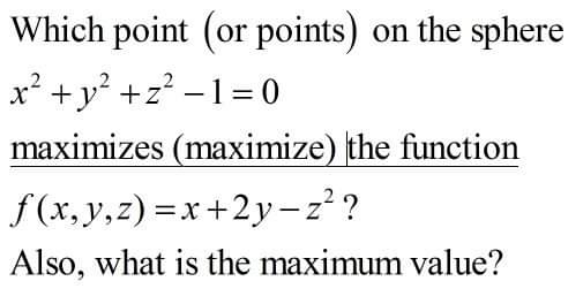
Question Number 152828 Answers: 1 Comments: 0
Pg 664 Pg 665 Pg 666 Pg 667 Pg 668 Pg 669 Pg 670 Pg 671 Pg 672 Pg 673
